HMC5883L电子罗盘的误差补偿系统设计※

张燕，陈华

（1.南京大学金陵学院，南京210089；2.南京五十中）

引 言

近年来，移动机器人的研究及相关技术应用得到了前所未有的发展。其中移动机器人研究的关键技术主要有三种，分别是避障、导航以及路径规划。

对未知环境中特别是一些动态环境下的环境辨识和自身定位是当前亟待解决的一个问题。定位技术能够获得在任何时刻移动机器人的相对位置，因此是实现导航和保证机器人自主导航的关键［1］，而移动机器人定位技术中角度信息的获取就非常重要。目前，常用来获取角度信息的传感器是电子罗盘以及陀螺仪，陀螺仪通过对角速度积分获取角度，存在的问题是容易产生零漂。电子罗盘一般情况下获取角度信息比较准确，但是遇到周围有磁场干扰的情况就会出现大的角度偏移产生误差。本文针对电子罗盘的角度如何纠正的问题进行了研究。

论文研究的平台是由陀螺仪L3G4200D、三轴MEMS加速度计ADX345、三轴电子罗盘HMC5883以及单片机ATmega128组成一个嵌入式姿态测量系统。在此系统获取的数据基础上编写了上位机软件，实现了各个传感器数据的分离，并对电子罗盘获取的角度信息如何纠正着重进行了研究。

1 系统结构

本系统主要由三轴数字陀螺仪L3G4200D、三轴MEMS加速度计ADX345、三轴电子罗盘HMC5883以及单片机ATmega128组成。嵌入式角度测量系统结构框图如图1所示。

图1 嵌入式角度测量系统结构框图

1 数据获取软件的设计

1.1 串口通信软件设计

姿态测量系统的陀螺仪、加速度计、电子罗盘数据通过I2C总线与ATmega128进行通信，下位机ATmega128通过串口将数据上传到上位机上。上位机采用LabWindows CVI软件编写代码实时读取串口数据且显示在界面上。显示界面如图2所示。

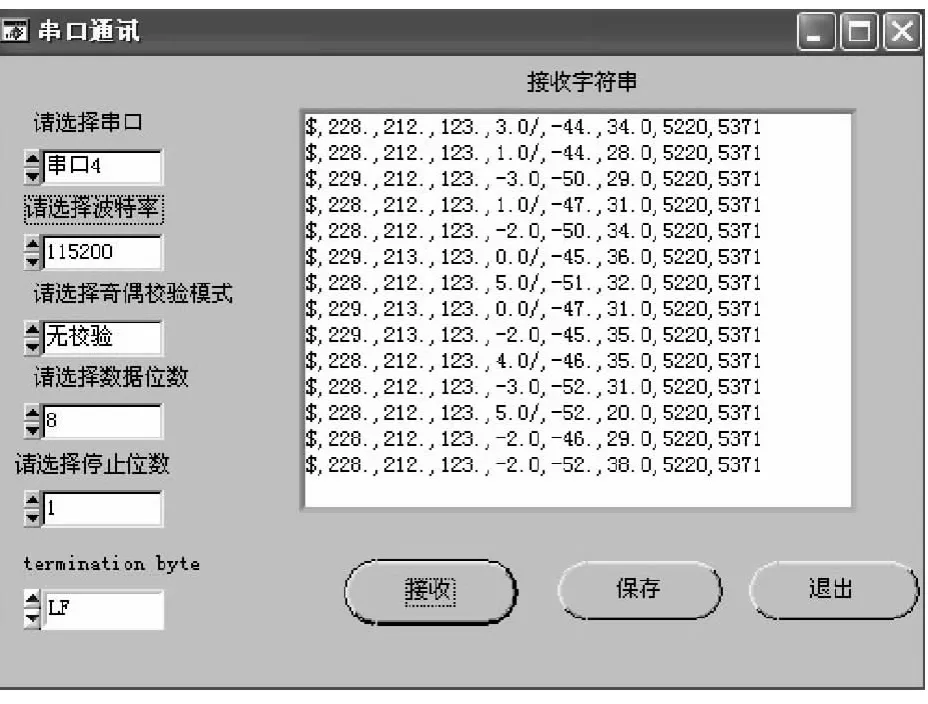
图2 上位机显示传感器数据

图2显示的数据是字符格式，下一步的工作便是编写代码将各个部分的数据分离出来。

1.2 数据分离代码的编写

对于单片机传输到上位机的数据设置的格式是：S罗盘角度、陀螺仪x轴角速度、y轴角度、z轴角速度、加速度计x轴加速度、y轴加速度、z轴加速度。

数据分离的流程图见图3。打开文件后，首先判断获取的字符是否是＄，如果不是则继续获取下一个字符，直到获取＄符号，接下来读取＄和“；”之间的数据，存储到字符数组中。接着读取各个“；”之间的数据存储到存储传感器各个数据的字符数组，直到读取的字符是回车符，重新读取第二轮数据存储到各个字符数组中，当读取的字符为文件结束符时结束文本读取。

图3 传感器数据分离流程图

2 电子罗盘数据误差修正

由于电子罗盘读取的数据受到周围磁场的干扰非常严重，需要对电子罗盘的数据进行修正，目前常用的电子罗盘纠正方式有椭圆假设法和八方向二乘法。

2.1 椭圆假设法

电子罗盘的误差主要包括硬铁干扰和软铁干扰。由于地磁场是弱磁场，并且地磁场可以认为在一定范围内是均匀的。硬铁干扰产生于永久磁铁或被磁化的金属，这种干扰与罗盘的相对位置固定，相当于在罗盘的输出值上增加了一个定值，使罗盘输出曲线图的圆心偏移了。软铁本身没有磁性，它被地磁场磁化后获得磁性，软铁干扰产生于地球磁场和罗盘附近的任何磁性材料之间的相互作用，其干扰程度与罗盘的方向有关，使罗盘的输出曲线畸变成一椭圆。［2－5］

4 磁方向角的定义

设电子罗盘有两个相互垂直的轴，分别称为OX 轴和OY 轴，如图4所示。Ψ 表示电子罗盘测得的磁方向角，定义为从ON 到OX 顺时针转过的角度。设地磁场的水平分量为H0，则磁场分量为Hx＝H0cosψ （1）Hy＝－H0sinψ （2）

ψ可以由ψ＝－arctan（C＝（Hy／Hx）求出。

当电子罗盘有误差时，就会反映在Hx和Hy的变化上。设有误差时Hx、Hy变为Hx1、Hy1，它们的关系可以写成：

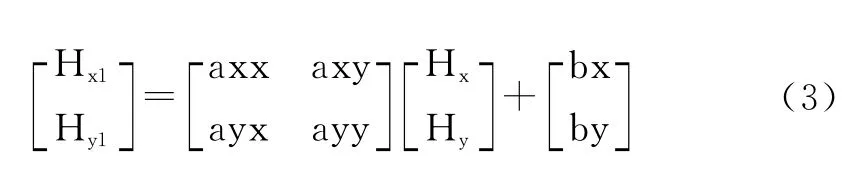
当角度从0°～360°变化一周时，Hx和Hy合成向量的顶点在平面上的轨迹是个圆，由于误差的影响，Hx变成了Hx1，Hy变成了Hy1，而Hx1和Hy1合成向量的顶点在平面上的轨迹不再是圆。为了确定该轨迹，我们提出椭圆假设，假设Hx1和Hy1合成向量的顶点在平面上的轨迹是个椭圆，则式（3）改写为：

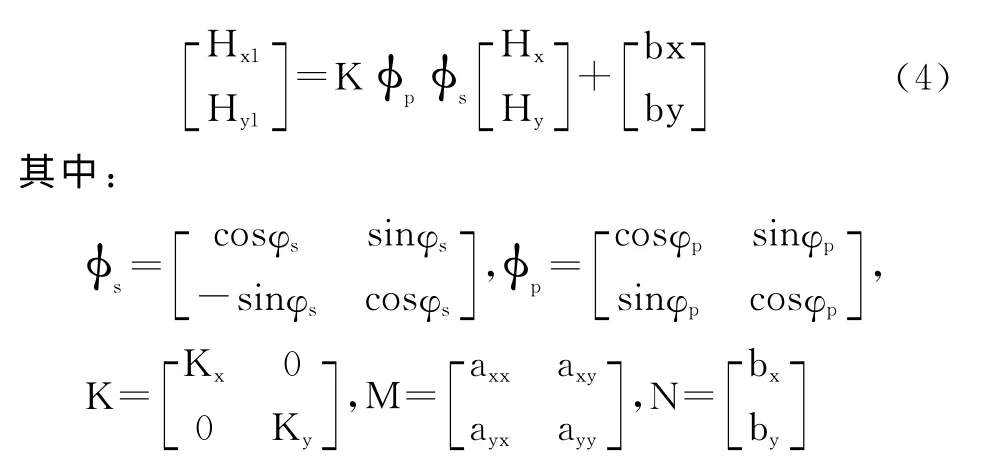
即假设对角阵K、正交阵φs和对称阵φp的乘积等于M，首先正交阵将圆转了一个角度φs，对称阵使圆变成一个椭圆，对角阵将椭圆转了一个角度φs，N 的作用是改变椭圆的中心位置。我们根据椭圆假设在某方向对电子罗盘采样一组数据Hx1和Hy1，其对应椭圆上的一点，则椭圆方程可以表示成：

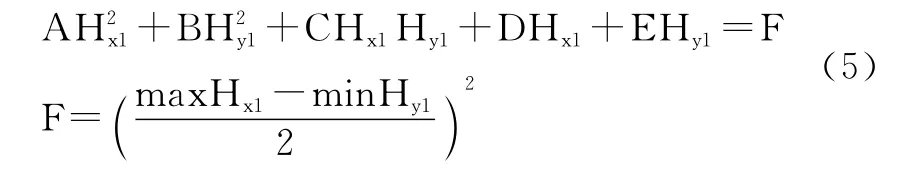
式（5）中有5个未知数，让电子罗盘在5个方向上采样数据，我们要求5个方向为均匀方向，即0°～360°采集0°、72°、144°、216°和288°这5个方向的数据。设采样数据为Hx1i和Hy1i（i＝1，2，…，5），根据式（5）可列出方程组

其中：

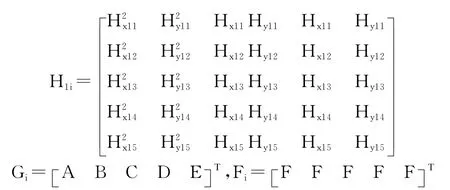
只要采样方向在0°～360°内大致均匀分布，方程组（6）就有唯一解A、B、C、D、E。它们与式（4）中各系数之间的关系为［6］：

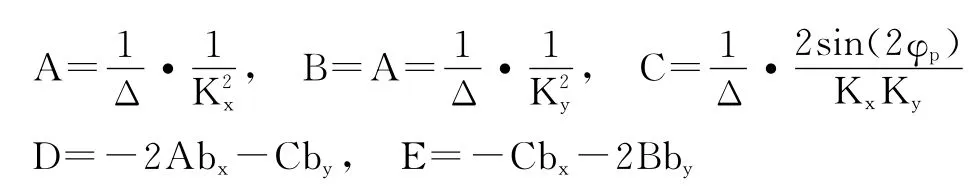
其中，Δ由采样数据求出，且

只要求出φp、Kx、Ky、bx、by，就可以把椭圆还原成圆。再根据式（4）求得补偿校正之后X 轴和Y 轴真实的磁场强度，从而求得准确的航向角。

2.2 八方向二乘法

最小二乘法是一种数据拟合建模法［7］，通常是用最小二乘法原理［8］及用最小化误差的平方和找到一组数据的最佳函数匹配，求出未知函数的最可信赖值作为测量结果。

基于八方向二乘法的电子罗盘误差补偿原理和实现：罗差是地磁场测量值时罗盘所固有的误差，其对测量精度的影响最大，同时在不同的测试环境下其值是变化的。罗差是由外界干扰而产生的航向误差，可以分为两大类：硬磁材料引起的罗差和软磁材料引起的罗差。

硬磁干扰可以认为是一种永久磁铁干扰，认为硬磁材料所引起的磁场是均匀分布的，其产生的误差在航向角0°～360°之间为近似正弦曲线，硬磁罗差△1表示：

式中：φ为补偿前罗盘的输出航向值，B、C 为罗差补偿系数。

软磁材料的本身是不产生磁场的，但是它会被周围的磁场环境给磁化，从而影响周围的磁场，它所引起的误差大小可以分解为两部分：一是圆周误差，二是象限罗差，用△2表示：

式中：A、D、E为罗差补偿系数。

综上所述，△φ表示总罗差，所以

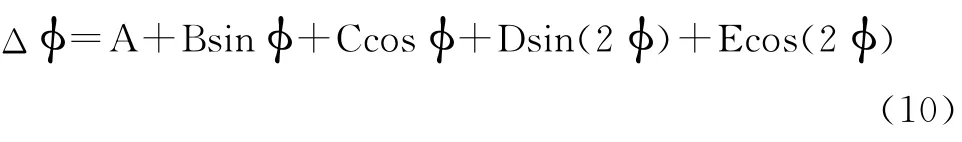
由以上分析可以得出，我们的主要工作是求出误差补偿系数，即A、B、C、D、E。具体方法如下：因为一共需要求5个值，为了计算方便，在0°～360°之间取5个实验点进行误差测量即可求出补偿系数，把后面测得的数据带入公式就可以得到精确的航向角。

记误差方程：

UC＝H

其中：

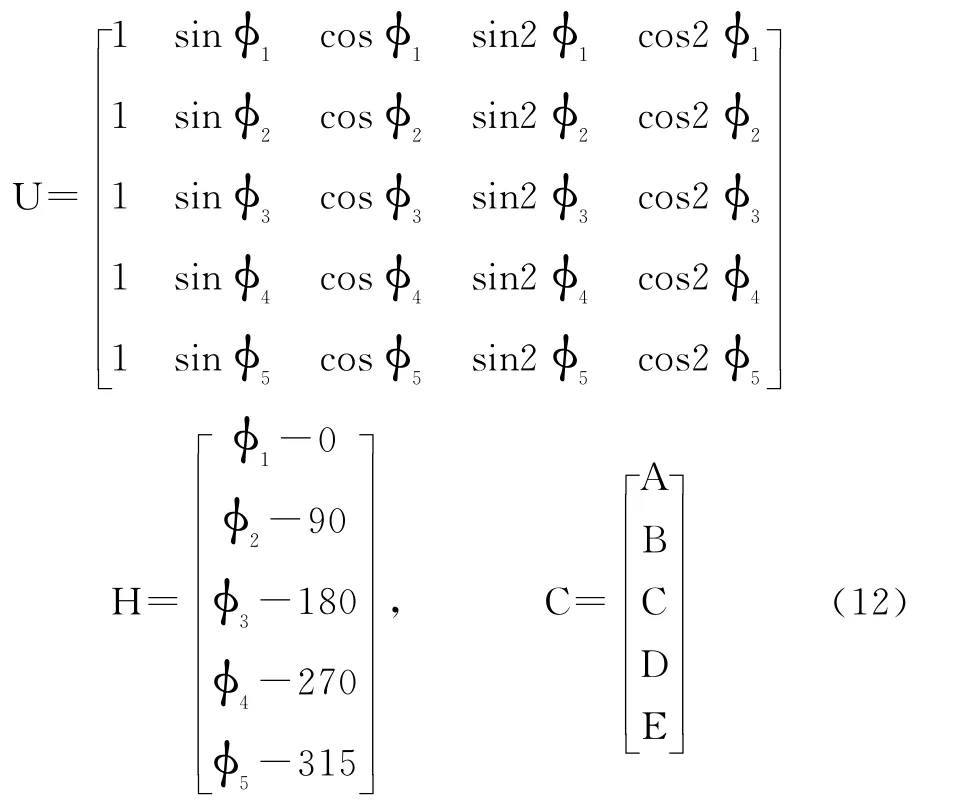
根据矩阵的性质，可以求出罗差的补偿系数：

3 实验结果以及分析

本文设计了一个完整的数据获取、存储以及电子罗盘数据纠正软件系统。运行系统首先显示的界面如图5所示，接收字符界面可以实时显示接收的数据，点击保存可以将数据存储到文本文件中。下面有两个按键，分别可以弹出电子罗盘角度进行纠正算法处理的两个界面。

图5 上位机串口接收界面

3.1 椭圆罗差法实验结果

点击图5中的“角度处理（椭圆罗差法）”按钮可以弹出如图6所示的界面。

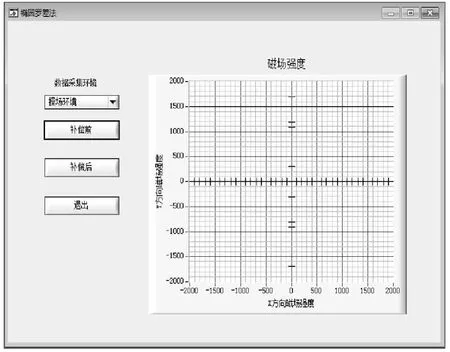
图6 椭圆罗差法显示界面

该界面可以选择数据采集环境，点击“补偿前”按钮可以从文本文件中读取电子罗盘采集的磁场信息，同时能够显示在某一环境下采集的磁场数据绘制的电子罗盘的磁场信息；点击”补偿后”按钮则可以绘制补偿后的磁场信息；点击“退出”按钮可以退出当前界面，回到主界面。

椭圆罗差法纠正数据对比图略——编者注。

3.2 八方向二乘法补偿数据实验结果

八方向二乘法数据显示界面略——编者注。点击“误差曲线”按钮可以显示数据处理前和处理后与实际数据的区别。点击“退出”按钮，可以退出当前界面、回到主界面。

图7中黑色粗线是纠正前读取的数据，黑色细线为电子罗盘纠正后的数据。从图中可以看出，在干扰较小的情况下，电子罗盘读出来的数据基本与实际数据吻合。

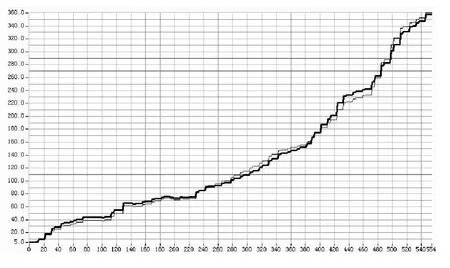
图7 八方向二乘法数据处理结果

结 语

本文设计了基于多传感器进行姿态测量的定位系统的上位机软件，可以实现下位机通过串口将传感器的数据传输到上位机功能，编写上位机显示界面显示下位机获取的数据。在此基础上研究了电子罗盘误差纠正的两种方式，并且编写代码实现了两种纠正算法的代码，在此基础上编写界面显示纠正算法的处理结果。实验结果显示，经过电子罗盘算法处理之后的数据能够比较准确地显示当前的数据信息。

编者注：本文为期刊缩略版，全文见本刊网站www.mesnet.com.cn。

［1］张燕，夏庆锋，谢鹏飞.基于多传感器的姿态测量系统设计［J］.机器人技术，2013（3）.

［2］蒋贤志.数字电子罗盘误差分析及较正技术研究［J］.现代雷达，2005，27（6）：39－40.

［3］Robert Smith，Andy Frost，Penny Probert.ASensor Sy stem for the Naviga tion of an Under water Vehicle［J］.The Interna tional Journal of Robotiics Research，1999，18（7）：697－710.

［4］张爱军，王昌明，赵辉.三轴电子罗盘的磁航向角误差补偿研究［J］.传感器与微系统，2008，27（8）：3－35.

［5］张静，金志华，田蔚风.无航向基准时数字式磁罗盘的自差校正［J］.上海交通大学学报2004，38（10）：1757－1860.

［6］刘诗斌、冯晓毅、李宏.基于椭圆假设的电子罗盘误差补偿方法［J］.传感器技术，2002（10）.

［7］马文.磁罗盘误差补偿及数据处理方法研究［D］.上海：上海交通大学，2006.

［8］张爱军，王昌明.赵辉.三轴电子罗盘的磁航向角误差补偿研究［J］.传感器与微系统，2008（8）.