基于Matlab与Modelsim 的四足机器人步态算法的协同仿真

罗庆生，李超，韩宝玲，司世才，牛锴

（1.北京理工大学 机电学院，北京100081；2.北京理工大学 机械与车辆学院）

罗庆生（教授）、李超（硕士研究生），研究方向为特种机器人技术、机器人伺服驱动技术。

引 言

我国广大山区地势险峻、地形复杂，轮式或履带式机器人很难在这些地区进行军事侦察、资源勘探、货物运载等工作。四足机器人具有较强的机动性和灵活性，能够适应非结构化的地面，有望在这些区域发挥机动性能，已成为移动机器人研究领域的热点之一。运动控制算法是四足机器人研究的重点和难点，如何验证控制算法的有效性，更好地应用于四足机器人的实际行走中是本文研究的重点。

笔者所在实验室设计了一种液压驱动的四足机器人，该机器人采用FPGA 作为步态算法的硬件平台，如何将步态算法快速有效地应用于FPGA 硬件板中成为研究的核心。传统的验证方法需要花费大量的时间将步态算法转换为硬件语言，并且在后期验证过程中需要系统开发人员以及FPGA 设计人员多次返工。而Simulink 仿真库里提供的HDL Coder功能，能够把Matlab／Simulink直接转化为Verilog 语言程序，同时可以生成仿真用的Test Bench，包括FPGA 和ASIC 的硬件设计流程无缝连接起来的联合仿真接口扩展模块，它的快速双向连接将Matlab／Simulink和硬件描述语言仿真软件Modelsim 连接起来，使二者之间直接的联合仿真成为可能，并且更高效地在Matlab／Simulink 中验证Modelsim 中的寄存器传输级（RTL）模型。因此笔者在文中采用了Matlab与Modelsim 协同仿真的方法，既降低了系统级开发的复杂度，又提高了设计的验证效率。

1 四足机器人控制模型建立

1.1 液压四足机器人物理样机介绍

笔者所在团队设计的四足机器人采用液压伺服驱动，现已设计并加工出该机器人的物理样机（见图1）。该四足机器人采用两腿节设计，共12个主动自由度，腿部含有3个旋转关节，分别为侧摆关节、髋关节和膝关节。3 个关节均采用液压缸驱动，通过对液压缸活塞杆的位置控制来实现机器人的各种步态。该机器人的总体长度为1m，宽度为0.5m，站立时高度为1m，其中足端距机体中心高度为0.74m。机器人的腿部采用前肘后膝的结构形式［7］，四条腿采用模块化设计，结构尺寸完全一致，其中大腿和小腿的长度均为400mm，侧摆关节到髋关节的距离为140mm。

图1 液压四足机器人物理样机

1.2 CPG控制方法简介

液压四足机器人采用基于CPG 和生物反射的控制方法。CPG（Central Pattern Generator，中枢模式发生器）是由中间神经元构成的局部网络，能够通过神经元之间的相互抑制产生稳定的相位互锁关系，并通过自激振荡激发肢体的节律运动（如跑、跳、游等），通过对其进行数学建模以产生控制信号实现四足机器人的典型步态。该方法避免了对动力学研究精确度的依赖，控制相对简单，具有良好的自稳定性，生物对复杂环境的适应性主要是通过各种反射机制实现的，观察生物反射行为，探索其反射机理，对反射动作进行规划和建模是提高四足机器人环境适应性的主要方法。

对四足机器人的运动进行控制，最基本的是建立合理的CPG 网络模型，产生持续稳定并且具有一定相位关系的多路周期性振荡信号，以控制四足机器人的各关节运动，使其可以在平地上完成几种典型步态下的运动。

1.3 液压四足机器人控制算法模型的建立

本文选择了加入反馈的Hopf振

荡器作为CPG单元模型，Hopf振荡器结构较简单，且能在一定程度上反映神经元间的关系，调节方便，参数对输出的影响简单，其数学表达式如式（1）所示。式中x、y为两个相互耦合的变量，使振荡器模型的输出在状态空间形成稳定极限环，a、b为定义极限环收敛时间的正常数，t是一个取较大值的正常数为x、y振荡的幅值，w为振荡器的振荡频率，wstance和wswing分别控制振荡器x输出上升和下降区间的持续时间（即分别代表支撑相和摆动相的频率）。

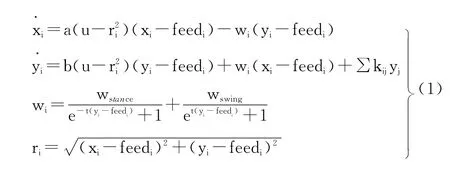
2 从Simulink模型到硬件描述语言的转换

2.1 Simulink模型的建立

Simulink是Matlab软件重要的软件包，在动态系统仿真中，它对于连续系统和离散系统、线性系统和非线性系统同时适用，采用模块直观地描述系统典型环节，可以十分方便地建立系统模型而不需要花大量时间编程。所建立的CPG 模型能否输出具有确定相位关系的控制信号，还需要进一步仿真验证，本文利用Simulink工具包对模型进行了数值仿真，采用odb3（Bogacki－Shampine）算法，仿真步长固定为0.005s。

建立如图2所示的CPG 单元模型，并且建立如图3所示的CPG 整体模型。

图2 CPG单元模型

2.2 高效转换工具

传统的FPGA 开发流程，要将已经在Simulink中实现的算法转换为FPGA 可识别的代码。首先需要将算法中的数据进行定点化处理，将浮点型变量转换为定点型；其次将算法用HDL代码形式实现出来，并对代码进行测试，发现问题并改正相应代码，直到测试通过；再次将HDL代码综合成逻辑网表，映射到FPGA 上的资源；最后在FPGA 上完成布局布线，并再次测试。传统的FPGA开发需要很长的开发周期，很难满足快速更新要求。

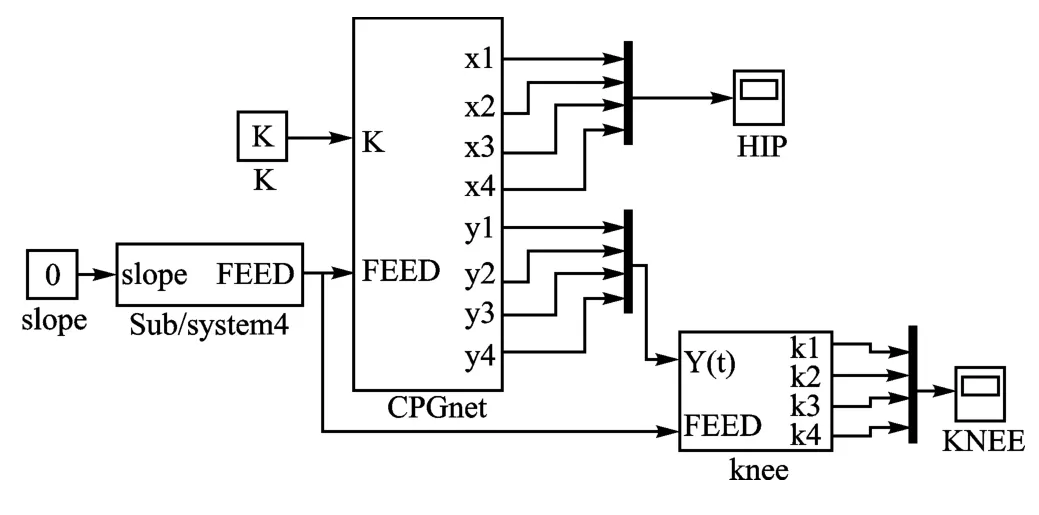
图3 CPG整体模型

基于模型设计，利用Matlab中的HDL Coder工具实现代码转换过程，如图4 所示。首先利用Mathworks的Matlab／Simulink的系统设计能力和无缝分析能力，以及已有的MegaCore完成顶层系统设计；接着通过转换工具配置Simulink中的IP核，即将静态参数做定点化处理；再将Simulink模型文件（.mdl）转换成VHDL 的RTL 表述和工具命令语言（Tcl）脚本，同时还可进行RTL级的功能仿真；然后通过SOPC 设计工具进行综合、适配与时序仿真；最后形成对指定FPGA 进行编程配置的文件，实现硬件系统的仿真测试模型。

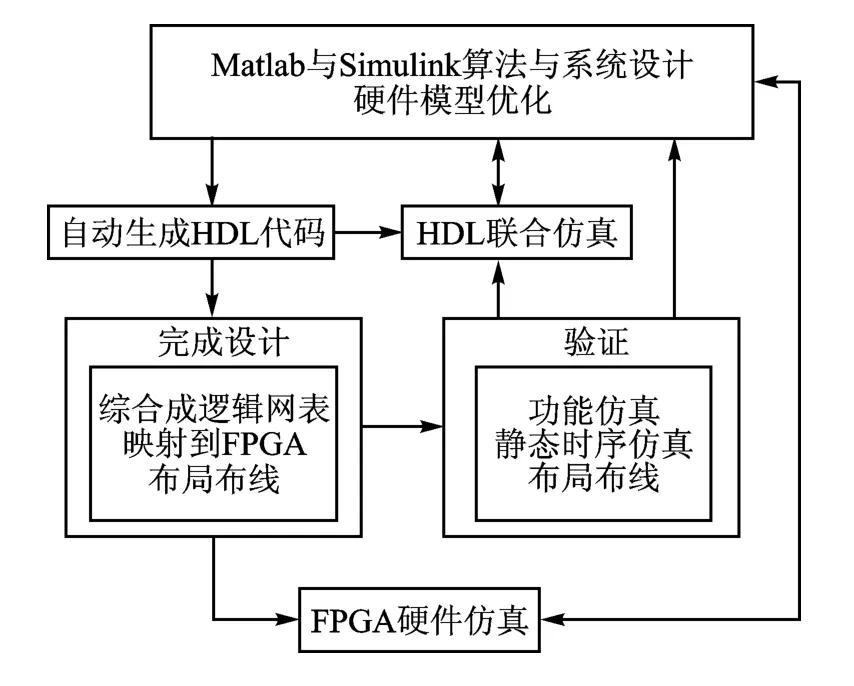
图4 采用基于模型设计加速的整个过程

2.3 Verilog代码生成

转换需要两个过程：第一个过程，审察整个设计并确定模型的公用模块，每一个公用模块都将被描述成一个单独的VHDL文件。从Simulink的基本模块中区分模型的次级模块，并采集每一个模块端口及端口类型的相关信息，在编写VHDL文件进行内容描述时将会用到这些信息。第二个过程，算法反复地检查模型的全部层次，从最高层次到底层，为每一个在第一个过程中找到的模块生成结构描述。HDL Coder不支持矩阵，对原模型做适当修改，将内部的矩阵相乘改为相乘相加的形式，运行模型中的.m 文件，并在Simulink中完成仿真。右键点击模型选择Fixed－Point Tool进入对话框，按照图5中右面步骤一步步完成定点转换。点击Fixed－Point Advisor打开定点向导，右键选择Run to Failure运行向导一步步验证，当出现错误或者警告时，按照提示做出相应调整。

完成定点转换以后，右键点击模型选择HDL Code下的HDL Code Properties进入图6所示对话框。HDL Coder支持代码自动生成，同时还可以生成仿真用的Test Bench，可以大大缩短验证时间，从而缩短设计周期。

图5 定点化处理

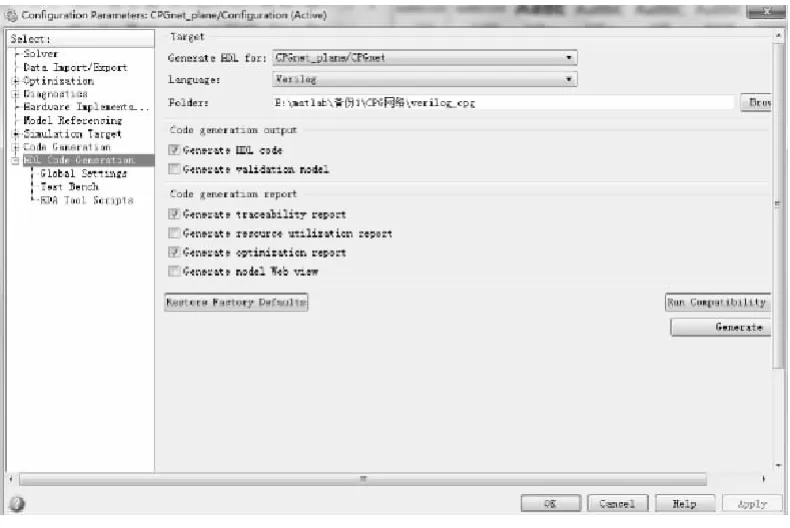
图6 HDL Coder代码自动生成

3 协同仿真验证

为了综合验证算法的有效性，生成代码以后还需要验证生成代码与Simulink模型的一致性。文中采用了协同仿真验证，本文借助Matlab内的HDL Coder功能协助生成测试脚本，完成相应的仿真验证。选择HDL Code Generation中的Test Bench，勾选HDL Test Bench和Cosimulation两个选项用于联合仿真，点击右下角的Generate Test Bench，生成测试脚本，同时产生用于联合仿真的模块，如图7所示。图7（a）为原Simulink模型，图7（b）是用于调用Modesim 对HDL代码进行仿真。

点击图（a）右上角模块打开Modesim，点击Simulink中的运行进行仿真。在Simulink适配器中产生数据波形如图8所示。上面为Modesim 输出的波形，下面为Simulink中输出波形，最后一个为两个之间的差值。如图能清晰地看出两个波形输出完全一致，验证了HDL 代码与Simulink模型完全一致。

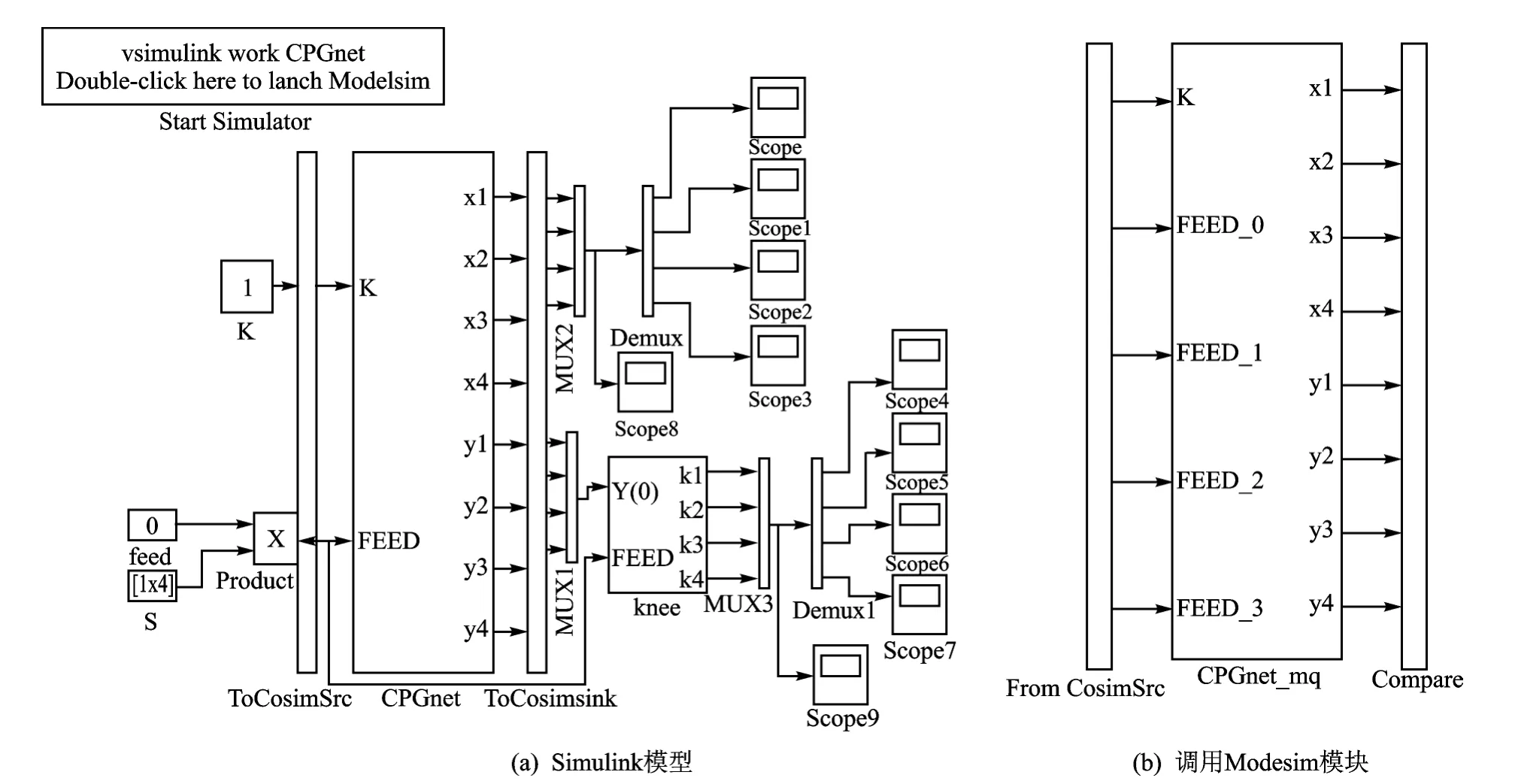
图7 联合仿真模块

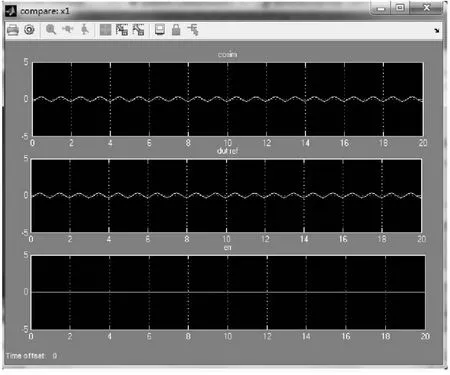
图8 输出效果对比图

结 语

为了验证四足机器人步态算法的可行性，采用Matlab与Modelsim 协同仿真的方法，力求通过联合仿真的方式实现验证的完整性。在Simulink中建立系统模型，完成初步仿真，使用了Matlab内的HDL Coder将Simulink模型自动转换为Verilog，实现FPGA 系统级的仿真。这既保证了代码的准确性，又节省了复杂的Test Bench编写过程，有效加快了仿真的速度，缩短了设计周期。最后借助Modelsim 实现仿真数据的前后对比，直观有效地验证了步态算法的有效性。

［1］郭云飞，孙福海.Modelsim 与Matlab／Simulink联合仿真技术研究及应用［J］.光电技术应用，2013，28（6）.

［2］刘杰.基于模型的设计—Qsys篇［M］.北京：机械工业出版社，2012.

［3］陈永春.从Matlab／Simulink模型到代码实现［M］.北京：清华大学出版社，2002.

［4］诸葛俊贵.基于Matlab模糊控制器HDL 代码的自动生成［J］.电子科技，2012，25（1）：42－44.

［5］杨守良.Matlab／simulink在FPGA 设计中的应用［J］.微计算机信息，2005，21（23）.

［6］Ying－Shieh Kung，Nguyen Vu Quynh.Simulink／ModelSim co－simulation of sensorless PMSM speed controller［J］.Proceedings 2011IEEE Symposium on Industrial Electronics and Applications，2011，24（9）.

［7］Hatnik U，Altmann S.Using ModelSim，Matlab／Simulink and NS for simulation of distributed systems［J］.International Conference on Parallel Computing in Electrical Engineering，2004（9）：7－10.

［8］杜勇，刘帝英.MATLAB在FPGA 设计中的应用［J］.电子工程师，2007（1）.

［9］胡迎刚.基于FPGA的DSP设计方法的研究［J］.工会博览·理论研究，2010（5）.