基于关联度的遗传-粗糙集约简算法

何新华，陆皖麟，陈庚申

(装甲兵工程学院信息工程系，北京 100072)

运用构建聚合仿真模型的方法对武器装备体系作战能力进行评估是当前武器装备体系作战能力评估的主流方法。在建立体系作战能力单元之后，如果直接运用所设立的作战能力单元构建体系作战能力聚合仿真模型，由于仿真模型涉及到的数据量十分庞大，模型聚合时繁重的计算量将是一个严峻的挑战。因此有必要在不影响聚合结果的前提下对聚合仿真所涉及的模型数据进行预处理，以达到提高仿真计算速度的目的。因此针对如何提高聚合仿真计算效率，本研究提出模型单元关联度的遗传-粗糙集理论的仿真模型优化算法实现对所构建体系作战能力模型进行约简。

1 现有约简理论

1.1 粗糙集理论

基于粗糙集理论的约简是处理目标属性简约问题的有效方法［1］。粗糙集约简的原理是运用信息映射函数，构建决策表中属性集的等价关系，以等价关系为支撑，实现对决策表的约简。通俗地讲，运用粗糙集约简理论进行对象约简，能够在确保约简对象最大信息量的情况下到达约简的目的。粗糙集属性约简的质量取决于信息映射函数 f拟定的质量。现有的粗糙集约简理论的分类主要是依据信息映射函数的不同进行划分的，对于粗糙集约简理论的划分［2-4］如图1所示。

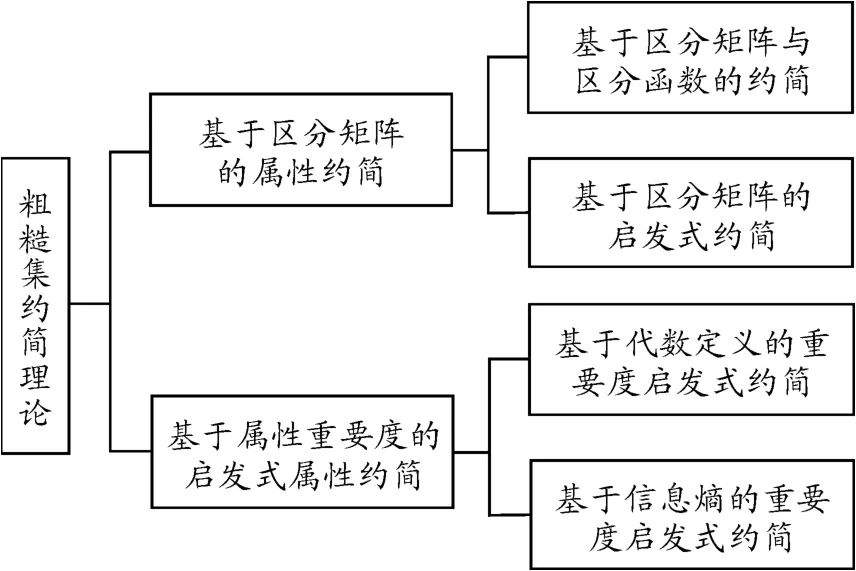
图1 粗糙集约简理论划分

“组合爆炸”和“局部最优”是粗糙集约简算法中普遍存在着的两大类问题。因此，如果单纯运用粗糙集约简算法对体系作战能力单元进行约简，存在这很大的算法局限性和不合理性。因此需要采用一种新的改良型粗糙集算法才能更好地解决体系作战能力单元约简问题。

1.2 遗传约简算法

遗传约简算法一般包括基本遗传约简算法［5］、基于信息熵的启发式遗传约简算法［6］、基于属性依赖度的启发式遗传约简算法［7］。

基本遗传约简算法通过求解最小约简值来达到约简的目的。算法的核心包括［8］:染色体编码和初代种群的定义、设置适应度函数、遗传运算和停止准则。通过算法可得到一个具有最大适应度的染色体。遗传算法在编码空间内操作而后得到染色体，但对于染色体的评估与选择则要在解空间中进行。因此需要对两个空间进行转化，最终得到最佳适应度染色体的解码即为最小约简。

基于信息熵的启发式遗传约简算法在传统遗传算法的基础上进行算法适应度函数的改进降低计算复杂度;增添一个局部修正策略来指导遗传算法的搜索空间，使得遗传算法的全局搜索能力进一步加强。

基于属性依赖度的启发式遗传约简算法则通过在适应度函数中引入属性依赖度降低遗传算法中适应度函数的计算复杂度。并改进遗传算法中初代种群的产生方式和引入一个最优保存机制。即初代染色体产生方式的改良主要体现在运用属性核的概念来约束随机产生初始种群染色体的生成方式;此外最有保存机制的本质是将适应度最差的个体逐步替换为适应度最优的个体。从而实现对于遗传约简算法的改进。

2 基于模型关联度的遗传-粗糙集约简算法

根据上节分析，本研究提出基于改良种群生成方式、算法适应度函数和优化各类遗传算子信息的约简思路。从文献对于上述算法运行结果分析可知，在以上3种遗传简约算法中，基于信息熵的遗传约简算法在约束搜索空间能力方面比另外2种算法更加实用。基于属性依赖度的遗传约简算法在算法复杂度和约简效率和结果方面拥有比其他2种算法更加理想的运行结果。如果将上述2种遗传算法进行进一步合理融合，新算法则可以在很大程度上满足体系作战能力单元约简的算法要求。因此，本研究提出基于改良种群生成方式、算法适应度函数和优化各类遗传算子信息的约简思路，提出一种基于关联度的遗传-粗糙集约简算法。

2.1 算法设计

基于关联度的遗传-粗糙集约简算法的基本设计思想为:在传统遗传算法的基础上进行改进，将单元属性关联度引入遗传算法适应度函数中，提高了算法的准确性，降低了算法的复杂度。同时，针对遗传算法局部寻优能力较弱、收敛较慢的特点，引入基于适应度函数的最优保存策略和局部修正机制对算法进行改良，从而使改进后的算法达到较好的约简效果。算法设计思想如下:

1)染色体编码。根据算法应用的对象，本算法采用二进制编码。单元约简的目的是确定单元的选择结果，二进制编码中的“0”和“1”恰好能充分对应于单元选择状态中的“未选中”与“被选中”。如，一个单元决策表中有7个条件属性，属性集为{c1，c3，c6，c7}，则在遗传算法中二进制编码表示为1010011。

2)初代种群。通常遗传算法在实际运用的过程中，对初代种群的设置一般为100～1000。但在单元约简的运用中，考虑到体系作战能力单元属性的实际情况，可将初代种群的数量界定为10～100。此外，根据单元的性质，应明确强调核单元这一概念，即所有单元约简的交集。核单元的定义，对染色体初始种群的生产加以限制，减少了初始种群产生的武目的性，从而提高了算法初始值的准确性，间接加快了算法的运行效率。

3)适应度函数。作为遗传约简算法的核心，适应度函数设计质量的优劣直接决定算法质量的好坏。因此对适应度函数的设计，本函数遵循2个设计原则:一是搜索空间为约简变量所在的值域中进行;二是搜索变量在约简单元中的数量尽可能少。依据此二原则，本算法采用基于属性依赖度的约简算法中适应度函数的形式

其中:m为条件单元集在染色体v中的个数;Lv为染色体v中二进制数字“1”的个数;k(0≤k≤1)为关联度，它表示相应的决策单元关联于染色体所代表的条件单元的程度。

4)遗传算子。遗传算法中运用遗传算子来体现算法优胜劣汰的思想。遗传算子包含3项操作，即选择操作、交叉操作和变异操作。选择操作选择优秀个体，淘汰较差个体的过程。运用轮盘赌法首先计算个体适应度总和，然后计算每一个个体的适应度，随后计算出相应个体遗传到新种群的概率。最后单个个体被算法选中的次数根据轮盘赌的方式确定;交叉操作是模仿生物学杂交，通过不同染色体上基因的交叉换位，产生出新的个体。不同染色体间是否交叉由遗传算法交叉率控制。根据4种交叉方法单点、双点、多点和算术交叉的各自特点，使用单点随机地选定种群中的2个个体，在2个个体上随机选取某一位置，按照预先设定的交叉概率Pc(0.4～0.99)完成交叉操作，获得一对新个体;变异操作是通过变异操作来避免算法过早收敛。首先定义变异概率Pm(0.0001～0.1)指定其中的变异点，随后就每一个变异点而言，对相应单元上的基因位数值进行取反操作，完成变异操作，获得新个体。

5)最优保存和局部修正。最优保存策略很好地解决了单元中核单元保存的需求。遗传算法中最优保存策略是避免最优个体被交叉、变异等操作所破坏，从而加快了算法的收敛速度。在本算法中，主要运用最优保存策略用单元集中的核单元将适应度数值最低的单元进行替换的操作。局部修正的目的是确保搜索一直在可行解的范围之内进行。因此在新种群产生后，需要运用局部修正策略对产生的若干个体进行修正和校验。具体做法为:对种群中单元属性关联度进行判断，若其判断数据是否为1，若为1则将该单元条件单元中处于搜索范围之外的单元重要度最高的单元加入搜索空间中来。

6)选择与终止策略。遗传算法所处理的许多实际问题不一定拥有最优解，但从科学的角度出发，算法不允许循环迭代无限次的进行下去，这就需要人为的限定算法的停止标准。在遗传算法中，一般采用2种停止策略:一是设定最大迭代次数，但算法迭代到设定的次数时，强制结束并输出结果;二是检测算法中产生的适应度函数值，当其数值在数次迭代中无变化则终止迭代，输出结果。2种方法相比而言，第一种拥有很大的人为主观性，因此在本算法中采取上文提到的第二种方法。

2.2 算法实现

依据上节的算法设计思想，基于关联度的遗传-粗糙集约简算法的具体流程描述如下:

Input:决策表 S=(U，A，V，f)，A=C∪D，C 为条件属性，D为决策属性。Output:S的一个约简R。

步骤如下:

步骤1:初始化初代种群。运用上文提到的核单元的概念约束初代种群pop(t)的产生，并令t=1。

步骤1.1:计算关联度r(C，D)。依据函数 r(C，D)计算出条件单元C相对于决策单元D的关联度。

步骤1.2:计算条件单元C的单元核Core。令Core=C，对于 a∈C，若 r(C-{a}，D)=r(C，D)，则 Core=Core∩{C-{a}}。

步骤1.3:定义初代种群。定义初 始 种 群 pop(t)由随机产生的p个长度为m的二进制串组成。同时，将Core的单元在二进制编码中对应位取“1”，其他单元对应为随机取“0”或“1”。

步骤2:计算单元相应染色体适应度值。依据步骤2对条件单元种群pop(t)中的每条单元染色体popi(t)进行其对于决策单元的关联度，随后将结果代入适应度函数fi=fitness(popi(t))中，从而得到每条染色体的适应度。

步骤3:执行选择操作。选择操作是遗传算法的核心，是优胜劣汰思想最主要的体现形式。其目的是将符合环境要求的优秀基因传递到下一代。

步骤3.1:执行最优保存策略。在算法进行轮盘赌的选择操作之前，算法会提前根据适应度值的大小选择其中数值最大的个体popmax(t)进行保存，使其跳过交叉、变异的操作直接进入下一代。

步骤3.2:执行轮盘赌选择操作。首先计算出所有染色体的适应度总和，依据此计算出每条染色体的相对适应度，即每条染色体被选中的概率。最后每条染色体被选中的次数运用模拟赌盘操作(即0到1之间的随机数)的方法加以确定，从而选择出新种群。

步骤4:执行交叉操作。首先定义交叉概率Pc，随后运用Pc对染色体进行操作，得到新种群pop(t+1)。

步骤5:执行变异操作。首先定义变异概率Pm，随后在核单元的对应位不发生改变的前提下，采用基本位变异方式对染色体进行操作，得到新种群pop(t+1)。

步骤6:修正校验并保存最优。经过遗传操作产生新种群pop(t+1)后，为得到更好的运算结果，需对pop(t+1)进行部分修正。传代最优个体。

步骤6.1:计算关联度r(R，D)，其中 R⊆C为新种群pop(t+1)所表示的单元集。如果r(R，D)=1，就执行步骤6.4，否则执行步骤 6.2 和步骤 6.3。

步骤6.2:将a从CR中挑选出来，即a∈CR，使单元重要度SGF(a，R，D)达到最大值，并将其设为ai。

步骤6.3:改变ai所对应的基因位，数值由“0”变 成“1”，加入到 R，即 R=R∪ai，则转入步骤 6.1。

步骤6.4:若r(R，D)=1，则计算此属性集R中每个属性aj的重要度 SGF(aj，R，D)，去除重要度为0的属性，得到算法的约简结果。

步骤6.5:终止修正，输出适应度值。

步骤6.6:执行最优保存。

步骤7:检验并执行终止条件。

依据上述算法步骤，基于关联度的遗传-粗糙集约简算法的流程图如图2所示。

基于关联度遗传-粗糙集算法特点体现在如下2个方面:

1)在传统遗传粗糙集约简算法中引入模型单元关联度并完成设计，首先实施初代种群的选取，即采用关联度引出核单元用于算法初代种群的产生，利用核单元约简交集，在初代种群对应基因位的随机产生中加以约束，避免了初代种群产生的盲目性，计算量大大降低，提高算法的搜索效率;然后利用适应度函数单元关联度降低算法适应度函数计算量;最后设定修正策略确保算法搜索始终在可行解的空间内进行，减小算法的盲目性。

2)运用单元适应度优化算法最优保存策略和算法终止条件，首先设计最优保存策略确保条件单元中适应度数值最大的单元可以顺利保留到下一代并取代适应度数值低的单元，达到约简效果，确保算法收敛性，使得约简算法更加符合武器装备体作战能力单元自身的基本特征，增加了算法的实用性;然后利用依据单元染色体适应度的特征给定“连续n代最优个体适应度不变则终止算法”的准则，避免了人工设定迭代次数所带来的主观性。

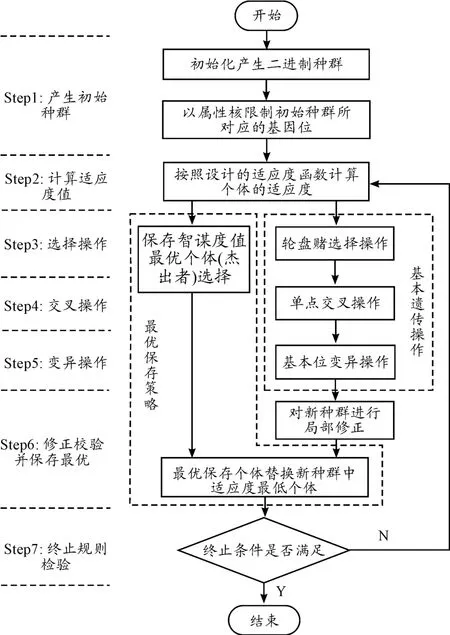
图2 算法流程

3 算法案例分析

对于约简算法的评估，一般从约简质量和约简效率2个方面进行［8］:约简质量通常从约简结果的有效性和条件属性压缩比的合理性两方面进行考量。约简结果的有效性指的是算法的运行结果包含重要属性，符合实际情况;条件属性压缩比的合理性指的约简程度科学合理，结果不包含边缘属性。约简效率通常从算法时间复杂度和收敛速度两方面进行考量。算法时间复杂度指的是算法运行一个周期所必需的计算复杂度，只有当复杂度处于合理的范围之内，算法运行速度才能在理想的状态下;算法收敛速度是指算法计算结果趋向稳态所需要的时间。

3.1 对比设计

为检验基于关联度的遗传-粗糙集约简算法的正确性与有效性，本研究提出的算法与基于信息熵的启发式遗传约简算法A［4］和基于属性依赖度的启发式遗传约简算法B［7］加以比较。实验环境:计算机配置为Intel CORE I5处理器，操作系统为 Windows 7，算法运行软件为 Matlab 7.0，内存为2G。

算法时间复杂度及收敛速度的检测实验分别运用3种不同的遗传约简算法对UCI机器学习数据集进行处理，比较3种算法的收敛速度。算法参数设置为种群规模30，交叉概率0.9，变异概率0.05，算法终止条件为连续3代平均适应度不变。约简数据设置如表1所示。

表1 UCI数据集的基本信息

3种算法对比:① 迭代收敛数据为:文献［4］中算法为34{X1，X4，X5，X9}，文献［7］中算法为 27{X1，X4，X5，X9}，本算法为15{X1，X4，X5，X9};② 数据集计算结果如表2所示。

表2 数据集计算

结果表明约简能力和算法有效性和压缩比有效，收敛速度和算法复杂度方面具有优势。

3.2 实例验证

以侦察预警探测能力为例展现算法实施过程。侦察预警探测能力可细分为:预警范围、预警目标种类、探测目标手段、有效探测时间、探测目标数量、目标发现概率、探测目标精度、目标属性识别率和虚警概率9个子能力，如表3所示。

在对侦察预警探测能力的各项子能力采集数据后，进行制作子能力量化决策表之前，需要对数据进行标准化处理。本文对数据标准化处理，依据上文所提到的“均值化”法。“均值化”法的具体操作为

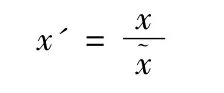
表3 侦察预警探测能力的9个性能指标

通过“均值化”法处理数据样本，使得所有子能力的样本值均在1～5之间。随后对侦察预警探测能力的9个子能力的300组样本进行分析，形成属性决策表，部分详表如表4所示。

表4 侦察预警探测能力所属各子能力的部分决策样本

首先，依据算法计算子能力单元关联度，确定出侦察预警探测能力子能力单元中的核子能力单元，将其所在的基因位强制定义为“1”。其余子能力单元随机设定基因位。经过计算，表4中核子能力单元为{X1，X4，X5}，即将此3个子能力单元基因位定义为“1”。随后对约简算法的各项参数进行设定为种群规模10，交叉概率0.5，变异概率0.02，算法终止条件为连续7代平均适应度不变，最终算法所得的最优个体为{110110100}，即子能力单元约简结果为{X1，X2，X4，X5，X7}。即将原来侦察预警探测能力中的9个子能力单元约简为5个，分别为:预警范围、预警目标种类、有效探测时间、探测目标数量和探测目标精度。同理，可将此算法应用到其他体系作战能力单元的约简中。通过此算法降低了聚合仿真计算量，提高了工作效率。

4 结论

在普通粗糙集约简算法的基础上，提出基于关联度的遗传-粗糙集约简算法。实验验证算法能有效地改善了聚合仿真模型的计算复杂度问题并且具有较好的实用性。

［1］冯林.一种基于量子遗传算法与粗糙集理论的属性约简法［J］.信息与控制，2011，40(2):198-201，213.

［2］郭春根.基于遗传算法的粗糙集属性约简研究［D］.合肥:合肥工业大学，2007:5-21.

［3］马翔，张继福，杨海峰.基于区分矩阵的启发式属性约简算法［J］.计算机应用，2010，30(8):1999-2002，2037.

［4］李华雄，周献中.基于0-1分辨矩阵的启发式属性约简［J］.中南大学学报:自然科学版，2009，40(S1):304-308.

［5］Wroblewski J.Finding minimal reducts using genetic algorithms［R］.Warsaw University of Technology，1995.

［6］Dai J H，Li Y X.Heuristic genetic algorithm for minimal reduct in decision system based rough set theory［C］//Proceedings of the First International Conference on Machine Learning and Cybernetics.Beijing:［s.n.］，2002:833-836.

［7］李旗号，赵卫东.遗传算法在决策表最小约简中的应用［J］.计算机工程，2001，27(2):80-81.

［8］UCI.UCI repository of machine learning database［EB/OL］.［2010-12-24］.http://www.ics.uci.edu/～ mlearn/MLRepository.html.