蛋糕超声波辅助切割刀的优化设计
2015-09-11张水田李远
张水田,李远
蛋糕超声波辅助切割刀的优化设计
张水田,李远
(华侨大学脆性材料加工技术教育部工程研究中心,福建厦门361021)
为了适应切割大尺寸、粘性食品的要求,设计了频率为20kHz的食品用超声切割刀。采用有限单元法对其进行模态分析,获取各阶固有频率、刀具刃口振幅分布等参数。通过对切割刀刀身结构进行敏感性分析,得到了切割刀结构尺寸对切割刀输出端位移的均匀性、纵向振动固有频率与邻近频率的影响。对影响程度大的结构参数进行了二次优化,使所设计的切割刀在20kHz频率附近以纵向振动模式为主,谐振频率与邻近固有频率间距足够大,刃口振幅位移分布均匀性得到较大的提高。
超声切割刀;谐振频率;优化设计;振幅分布
0 引言
蛋糕食品工业中,超声辅助切割刀由于不需要锋利的刃口和很大的压力,被切割材料不易造成撕裂、破损、变形、黏刀等现象而得到广泛的应用[1]。
文献[2,3]对高性能合金、复合材料、脆性材料辅助加工技术进行了研究。周胜利等曾对超声波切割刀进行研究,设计一种切割刀并建立了动力学模型和结构优化程序[4]。李丽等对烧结NdFeB材料工件利用超声旋转加工方法进行了组合振动加工,延长了工具的使用寿命[5]。但是已有超声振动辅助工具的加工对象大部分为工程材料,对于蛋糕等软质材料的超声振动辅助工具的设计方法研究较少。
超声切割设备基本构成是超声波发生器、换能器、变幅杆、切割刀(工具头)。在切割材料时,切割刀将变幅杆传递的机械能施加给被加工材料,得到高质量的切割效果[6]。传统的设计理论借助经典理论出发计算结构尺寸[7]。实际生产中,由于切割对象体积比较大,需要合适的厚度与宽度的切割刀,计算复杂。本文利用有限元软件ANSYS设计了纵向振动的振型纯净、刃口振幅位移分布均匀、谐振频率精确的切割工具。
1 切割刀基本结构的设计
本文以250 mm的圆柱型蛋糕作为切割对象。设计目标频率(1)为20 kHz,纵向振动振型。切割刀尺寸为,,、、。如图1所示,材质选用食品级奥氏体不锈钢316L。
1.1 振型识别
蛋糕用切割刀外形类似平板,这类结构具有密频特性。通过有限元软件,许多学者分析了类似结构的多维耦合振动形式,完成结构的优化[8-10]。本文对切割刀的模态进行分析发现,切割刀存在许多阶模态,不同的模态对应不同的振型和不同的固有频率。当切割刀的结构尺寸发生变化时可能导致模态阶次和振型发生改变,这样不利于ANSYS分析。因此,对切割刀进行优化设计首先要识别各阶模态,并能够提取对应的固有频率。
1.2 狭槽数量的确定
为了减少横向振动、提高刃口振幅位移分布均匀性、避免临近振型的干扰,通过在切割刀上开一些狭槽和改变大端的结构来实现。利用ANSYS有限元软件的优化设计模块可以准确确定狭槽数量。首先,参数化建立切割刀模型。选择solid186实体单元,采用自由网格划分方法划分单元格,当切割刀结构变化,单元可以自由延伸。Solid186单元为20节点弹塑性固体单元,具有塑性、蠕变、应力刚度、大变形和大应变能力。316L的属性:密度,弹性模量,泊松比。
(1)优化变量设置
切割刀数学模型的目标函数为,状态变量分别为1、2、3。具体含义定义如下:
均匀性:输出端纵向位移最小值/最大值;
频率间隔1:纵向振动的谐振频率与20 kHz差值的绝对值;
频率间隔2:纵向振动的谐振频率与纵振的下一阶频率差值的绝对值;
频率间隔3:纵向振动的谐振频率与纵振的上一阶频率差值的绝对值
设计变量为狭槽的数量,然后选择优化工具和优化方法,指定优化循环控制方式,并进行优化分析。
(2)结果分析
求解完成后可得到狭槽数量对纵向振动的振型固有频率的影响如图2所示,对频率间隔的影响如图3、4所示,对输出端均匀性的影响如图5所示。
由上述结果分析,当切割刀具有4或5个狭槽时,其具有较高的均匀性,为最优值。其对频率间隔的影响类似,由于4个狭槽时结果较简单,1较小,所以选择4为狭槽数目。此时由于开槽改变了切割刀结构,且2和3小于500 Hz,纵振振型易受附近模态干扰;产生纵向振动的谐振频率与目标频率也相距甚远。因此接下来,在确定了狭槽数量的基础上,通过改变狭槽相对之间的距离、结构尺寸、旋转角度以及切割刀输入端形状,进一步优化切割刀的结构,使其符合生产要求的刃口均匀性、频率间隔和接近目标频率。
2 切割刀结构的敏感性分析
开槽和改变大端结构后的切割刀形状比较复杂,各个结构尺寸的改变对切割刀振动特性的影响程度各异。进行二次优化时,为了较易获得切割刀的最优解,可以选取对其振动特性敏感性高的结构作为设计变量。通过对切割刀结构尺寸的敏感性分析,可以得到其结构变化对切割刀固有频率、频率间距、均匀性等振动特性的影响程度。为优化设计时提供选择设计变量的依据。经过机械加工和热处理等工艺,切割刀实物的振动特性存在不可避免的误差,因此,分析结果也可以为切割刀的修正提供依据。切割刀敏感性分析选取的结构如图6所示。
通过敏感性分析,分析切割刀结构对、1、2、3的敏感性,结果如图7~10所示。
切割刀的结构中对纵向振动谐振频率影响比较大的依次为3、2、1、1、2、2。其中,随着3、2、1、2、2尺寸的增大,纵向振动谐振频率减小;随着1尺寸的增大,纵向振动谐振频率增大,如图7所示。
切割刀结构中对纵向振动谐振频率与前一阶模态的频率间隔影响比较大的依次为1、3、2、、3、2、1、2、2、1。其中,1、2、、3、2、1、2、2随着以上尺寸的增大,频率间隔减小,3、1随着以上尺寸的增大频率,间隔增大,如图8所示。
切割刀的结构中对纵向振动谐振频率与后一阶模态的频率间隔影响比较大的依次为2、3、2、2、1、1、1、2、1。其中,随着2、3、2、2、1、1、1、2、1尺寸的增大,频率间隔增大;随着1、2尺寸的增大,频率间隔减小,如图9所示。
切割刀的结构中对输出端均匀性影响比较大的依次为1、1、2、1。其中,随着1、1尺寸的增大,均匀性增大;随着1、2尺寸的增大,均匀性减小,如图10所示。
3 优化设计
根据敏感性分析计算结果,二次优化选取的切割刀设计变量主要有:1、1、2、3、1、1、1、1、2、2、2、2、1、3。状态变量有:1、2、3;约束状态变量上下限,得到精确的谐振频率和单一的纵向振动振型。目标函数:。优化方法选择:函数逼近法(子问题近似法),优化流程如图11所示。
图12为优化设计后切割刀纵振振型示意图,云图颜色代表不同的位移值,可见切割刀刃口位移具有较高的均匀性。图13为纵振振型模态时刃口的位移振幅分布图,得到切割刀的均匀度为0.93。振动特性分析结果如表1所示,可以看出切割刀的纵向振动的谐振频率为20019 Hz,与目标频率20000 Hz误差为0.01%,频率间隔均大于500 Hz,即优化后的切割刀谐振频率精确,且具有纯净的纵向振动振型。
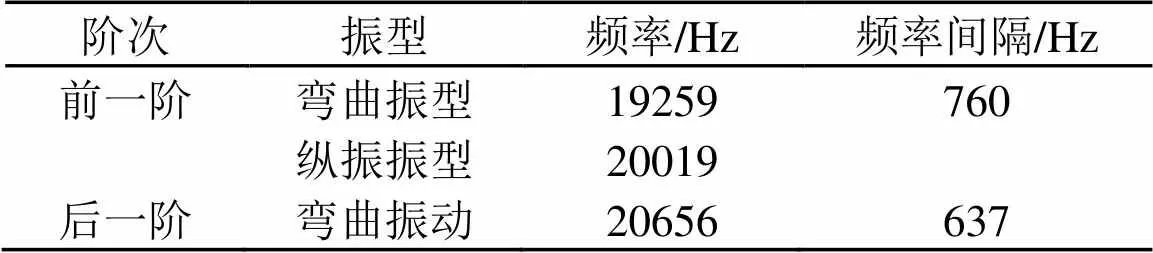
表1 最优解切割刀的模态
4 结论
(1) 分析了切割刀上开狭槽的数量对纵向振动的谐振频率,刃口位移分布均匀性的影响,结果表明,狭槽数量为4时均匀性较好。
(2) 分析了超声波辅助切割刀结构参数对切割刀谐振频率和纵向振动时刃口位移分布均匀性的敏感性。为二次优化时设计变量的选取提供依据。
(3) 通过有限单元法优化设计切割刀,满足纵向振动的谐振频率、刃口位移分布均匀性的要求。
[1] Susann Zahn, Yvonne Schneider, Harald Rohm. Ultrasonic cutting of foods: Effects of excitation magnitude and cutting velocity on the reduction of cutting work[J]. Innovative Food Science and Emerging Technologies, 2006(7): 288-293.
[2] 赵福令, 冯冬菊, 郭东明. 陶瓷材料旋转加工技术[J]. 电加工与模具, 2001(1): 1-5.
ZHAO Fuling, HONG Dongju, GUO Dongming. Ceramic materials processing technology[J]. Electromachining and Mould, 2001(1): 1-5.
[3] 任宇江, 郭东明. 碳纤维复合材料的超声辅助磨削加工技术研究[D]. 大连: 大连理工大学.
REN Yujiang, GUO Dongming. Study on the ultrasonic assisted grinding technology of carbon fiber reinforced plastics[D]. Dalian: Dalian University of Technology.
[4] 周胜利, 姚志远, 沙金. 超声切割刀动力学分析和结构优化设计[J]. 中国机械工程, 2013, 24(12): 1631-1635.
ZHOU Shengli, YAO Zhiyuan, SHA Jin. Dynamics analysis and structural optimization design of an ultrasonic cutter[J]. China Mechanical Engineering, 2013, 24(12): 1631-1635.
[5] 李丽, 张建华. 烧结NdFeB材料工件加振的超声旋转加工的研究[J]. 机械设计与研究, 2005, 21(2): 61-63.
LI Li, ZHANG Jianhua. A study on rotary ultrasonic machining aided by work piece vibration for sintered NdFeB[J]. Machine Design and Research, 2005, 21(2): 61-63.
[6] 刘莉, 邵华, 贾文友. 超声技术在食品加工中的应用[J]. 声学技术, 2012, 31(1): 89-91.
LIU Li, SHAO Hua, JIA Wenyou. Application of ultrasonic technique in food processing[J]. Technical Acoustics, 2012, 31(1): 89-91.
[7] 林中茂. 超声变幅杆的原理和设计[M]. 北京: 科学出版社, 1987, 53.
LIN Zhongmao. The principle and design of ultrasonic horn[M]. Beijing: Science Press, 1987, 53.
[8] 莫喜平. ANSYS 软件在模拟分析声学换能器中的应用[J]. 声学技术, 2007, 26(6): 1279-1290.
MO Xiping. Simulation and anlysis of acoustics transducers using the ANSYS software[J]. Technical Acoustics, 2007, 26(6): 1279-1290.
[9] 刘井权, 闫永春, 杨士勤. 超声切割系统的模态分析[J]. 哈尔滨工业大学学报, 2001, 33(4): 435-439.
LIU Jingquan, YAN Yongchun, YANG Shiqin. Modal an alysis of ultrasonic knife cutting system[J]. Journal of Harbin Institute of Technology, 2001, 33(4): 435-439.
[10] 付志强, 林书玉. 大尺寸余弦形超声变幅杆的设计[J]. 声学技术, 2008, 27(5): 765-769.
FU Zhiqiang, Lin Shuyu. Design of cosine type ultrasonic transformers[J]. Technical Acoustics, 2008, 27(5): 765-769.
The structural design of ultrasonic cutter for cakes
ZHANG Shui-tian,LI Yuan
(,,361021,,)
An ultrasonic cutter of 20 kHz for food is designed to meet the demand of cutting large viscoelastic food. By analyzing its model with the finite element method, the natural frequencies of all orders and the distribution of displacement amplitude of cutter edge are obtained. The influence of the structure size on the uniformity of displacement at the output port, the longitudinal natural frequency of vibration and the adjacent frequency are analyzed. The structural parameters with high sensitivities are redesigned to make the cutter dominated by the longitudinal vibration near 20 kHz. The interval between the resonant frequency and the natural frequencies is large enough, and the distribution of displacement amplitude on the cutting edge surface is greatly improved.
ultrasonic cutter, resonant frequency, optimal design, amplitude distribution
TH113.1
A
1000-3630(2015)-02-0152-05
10.16300/j.cnki.1000-3630.2015.02.010
2014-03-26;
2014-05-25
长江学者与创新团队发展计划(IRT1063)、新世纪优秀人才支持计划(NCET-11-0852).
张水田(1988-),男,河南驻马店人, 硕士,研究方向为高效精密加工。
张水田, E-mail: 577127345@qq.com
