特征值与特征向量考研题型分析

王莲花，杨伏香，徐明洁

（1.北京物资学院信息学院，北京 101149；2.河南水利与环境职业学院数学教研室，河南郑州 450008；3.河南教育学院教务处，河南郑州 450046）

特征值与特征向量考研题型分析

王莲花1，杨伏香2，徐明洁3

（1.北京物资学院信息学院，北京 101149；2.河南水利与环境职业学院数学教研室，河南郑州 450008；3.河南教育学院教务处，河南郑州 450046）

分析近几年线性代数有关特征值和特征向量考研试题，归纳相关题型，强调理解数学基本概念及培养灵活运用数学知识解决问题的重要性.

特征值；特征向量；相似对角化；正交变换；二次型

矩阵的特征值和特征向量是线性代数的核心内容之一，也是全国硕士研究生考试的重点之一，不仅出题较多，而且分值较大.因此，无论是授课教师还是考研学生都要给予充分的重视.矩阵的特征值和特征向量常与矩阵多项式的特征值、行列式、相似对角化和化二次型为标准形等知识点结合在一起进行考核，从每年的考研试题来看，要解决好相关问题均需要有清晰的数学概念、扎实的基本功以及灵活的解题技巧.下面结合近几年全国硕士研究生入学统一考试数学三试题为例，分析有关特征值和特征向量的主要题型及涉及的主要知识点，指出理解数学基本概念和培养灵活运用数学知识解决问题的重要性.

1 根据矩阵的特征值求与之相关矩阵的特征值或行列式问题

2 根据矩阵的特征值和特征向量讨论矩阵的相似对角化问题

例2 设A为4阶实对称矩阵，且A2+A=O，A的秩为3，则A相似于（ ）［2］.

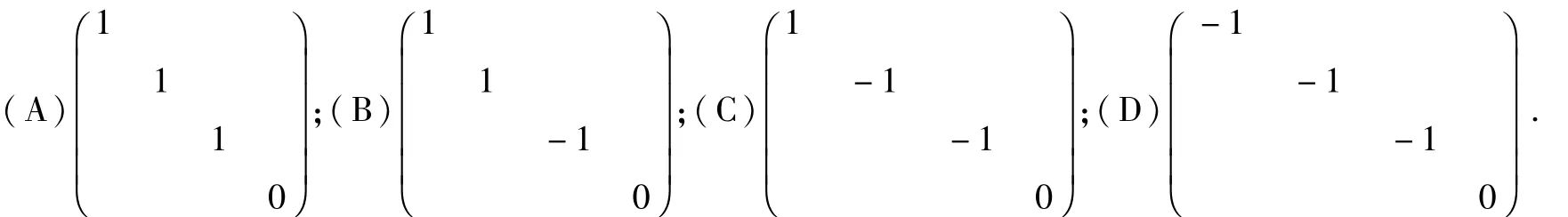
考查知识点及解题思路分析：根据例1的知识点求出A的特征值，再根据实对称矩阵一定与它的特征值组成的对角矩阵相似及相似矩阵具有相同的秩，就可以确定选项.

解设λ为A的特征值，由A2+A=O，所以λ2+λ=0，即（λ+1）λ=0，所以A的特征值为-1或0.又A为4阶实对称矩阵，故A可以对角化，即A～Λ.

考查知识点及解题思路分析：本题是一个综合性试题，虽是证明，实则计算题，该题综合考查如下知识点：①矩阵特征值的求法；②实对称矩阵必与特征值组成的对角阵相似；③齐次线性方程组（λE-A）x=0的基础解系含有n-r解向量，其中r=r（λE-A）；④n阶矩阵A可对角化的充要条件是A有n个线性无关的特征向量；⑤相似具有传递性.按照这个思路，本题容易得到证明.

3 根据矩阵的特征值和特征向量化二次型为标准形问题

4 根据矩阵的特征值和特征向量反求矩阵问题

考查知识点及解题思路分析：本题考查求矩阵的特征值和特征向量知识；实对称矩阵必可以对角化，对角化矩阵的对角线上的元素即为矩阵的特征值.而变换矩阵则由特征值对应的特征向量组成.本题所涉及的知识均是常考的知识点，属于基本类型.

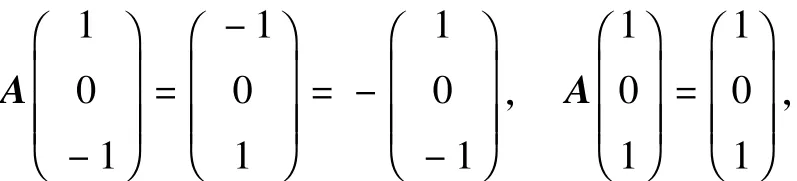
解（1）由于A的秩为2，故0是A的一个特征值.由题设可得所以-1是A的一个特征值，且α1=（1，0，-1）T是属于-1的一个特征向量，故属于-1的所有特征向量为k1α1（k1≠0）.

综上所述，矩阵的特征值和特征向量是考研的重要内容之一，不仅有分值为4分的选择题和填空题，而且有分值为11分的解答题和证明题.要想轻松解出这些题目，需要熟练掌握如下3方面的基本内容：①特征值、特征向量的概念和性质；②相似矩阵的定义、性质及矩阵可对角化的条件；③正交变换化二次型为标准形的相关理论.同时，还要具有较扎实的基本功，以确保在计算时既快捷又不出差错，再加上灵活的解题技巧，才能取得理想的成绩.

［1］ 233网校.2015年全国硕士研究生入学统一考试数学三试题［EB/OL］.［2015-01-06］.http：//www.233.com/newsfiles/2014-12/29/ 00000/.jpg.

［2］ 教育部考试中心.全国硕士研究生入学统一考试数学考试大纲：2011版［M］.北京：高等教育出版社，2010.

［3］ 教育部考试中心.全国硕士研究生入学统一考试数学考试大纲：2013版［M］.北京：高等教育出版社，2012.

［4］ 教育部考试中心.全国硕士研究生入学统一考试数学考试大纲：2015版［M］.北京：高等教育出版社，2014.

［5］ 教育部考试中心.全国硕士研究生入学统一考试数学考试大纲：2012版［M］.北京：高等教育出版社，2011.

［6］ 教育部考试中心.全国硕士研究生入学统一考试数学考试大纲：2014版［M］.北京：高等教育出版社，2013.

The Topic Analysis on M atrix Eigenvalues and Eigenvectors of the Nationw ide M aster’s Entrance Exam ination

WANG Lian-hua1，YANG Fu-xiang2，XU Ming-jie3

（1.College of Information，Beijing Wuzi University，Beijing 101149，China；2.Department of Mathematics，Henan Vocational College of Water Conservancy and Environment，Zhengzhou 450008，China；3.Academic Adm inistration，Henan Institute of Education，Zhengzhou 450046，China）

The test questions on matrix eigenvalues and eigenvectors of the nationwide master’s entrance exam ination are analysis and summarized.The importance of understanding basic mathematics concepts and applyingmathematics flexibly is emphasized.

eigenvalues；eigenvectors；similarity diagonalization；orthogonal transformation；quadratic form

O172. 2；G642.0

A

1007-0834（2015）03-0054-05

10.3969/j.issn.1007-0834.2015.03.014

2015-03-04

北京市信息类特色专业建设资助项目（PXM 2015-014214-000039）

王莲花（1964—），女，河南宁陵人，北京物资学院信息学院教授，硕士生导师，主要研究方向：代数及其应用.