立足例题拓展提升学习能力

薛小霞

圆是平面几何图形中最完美的图形，它既具有轴对称性，又具有任意角度的旋转对称性.本章“对称图形——圆”就是在直线型图形有关性质和判定的基础上，进一步探索“最完美”曲线型图形——圆的有关性质.下面就本章的两个重点——圆周角定理以及直线与圆的位置关系作一定的例题拓展.

1. 圆周角、圆心角是本章中最基本、最常见的角.

圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半，同弧或等弧所对的圆周角相等.

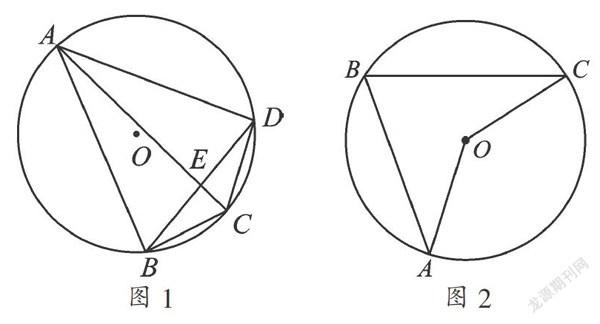
例1 （2014·湖北宜昌）如图1，点A、B、C、D都在⊙O上，AC、BD相交于点E，则与∠ABD相等的是（ ）.

A. ∠ACD B. ∠ADB

C. ∠AED D. ∠ACB

【解析】∵⊙O中，圆周角∠ABD所对弧是弧AD，而弧AD所对的圆周角还有∠ACD，∴选项A正确.

例2 （2013·江苏无锡）如图2，A、B、C是⊙O上的三点且∠ABC=70°，则∠AOC的度数是（ ）.

A. 35° B. 140°

C. 70° D. 70°或140°

【解析】∵⊙O中，∠ABC、∠AOC分别是弧AC所对的圆周角、圆心角，∴∠AOC=2∠ABC，∴选项B正确.

变式1 （2014·江西南昌）如图3，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为（ ）.

A. 40° B. 45° C. 50° D. 55°

【解析】∵⊙O中，圆周角∠B所对弧是弧AC，∴要用圆周角定理必须找弧AC所对的圆周角或圆心角，∴连接OC，则∠AOC就是弧AC所对的圆心角.

∵AO∥DC，∴∠ODC=∠AOD=70°，

∵OD=OC，∴∠OCD=∠ODC=70°，

∴∠DOC=40°，∴∠AOC=110°，

∴∠B=55°. ∴选项D正确.

【点评】以上三题考查圆周角定理，同学们要注意掌握同弧或等弧所对的圆周角相等且等于它所对弧上圆心角度数的一半.中考中圆周角定理经常出现，但单独考查它的题目不多，大多隐含在其他知识点中.

变式2 （2013·湖南张家界）如图4，⊙O的直径AB与弦CD垂直且∠BAC=40°，则∠BOD=________.

【解析】∵⊙O中，∠BAC是弧BC所对的圆周角，而∠BOD是弧BD所对的圆心角，由垂径定理可得弧BC、弧BD是等弧，∴∠BOD=2∠BAC，∴∠BOD=80°.

变式练习 （2014·内蒙古赤峰）如图5，AB是⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=65°，则∠BOC是（ ）.

A. 25° B. 50°

C. 130° D. 155°

变式3 （2013·江苏南通）如图6，Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是弧AB的中点，CD与AB的交点为E，则CE∶DE等于（ ）.

A. 4 B. 3.5 C. 3 D. 2.5

【解析】Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，可知Rt△ABC斜边（⊙O的直径）为5. D是弧AB的中点，可知“弧AD”、“弧BD”是等弧. 问题“CE∶DE”提醒我们要找含CE、DE在内的相似三角形.

【点评】本章的知识覆盖面较大，这就要同学们不仅能掌握圆的基本知识，还能综合运用圆与直线型图形的知识解决相关问题.对于这一类综合性比较强的数学问题，同学们要抓住已知条件进行联想，得到一些结论，同时也要把未知向已知转化，这样就能一步步突破.

2. 直线与圆的位置关系有3种.

设圆的半径为r，圆心到直线的距离为d，则

直线与圆相交？圳0≤d

直线与圆相切？圳d=r，

直线与圆相离？圳d>r.

其中，相切是3种位置关系中最特殊的一种，下面就切线的性质和判定作进一步学习与拓展.

【解析】连接OA，∵PA是⊙O的切线，我们可得△OAP是直角三角形，由勾股定理得OA=10 cm，

∴⊙O的周长为2πr=20π，

∴选项C正确.

【点评】运用切线的性质来进行计算或说理的常见辅助线是连接圆心和切点，利用垂直构造直角三角形解决有关问题.

例4 如图9，AD平分∠BAC，P是AD上一点，过点P作PE⊥AC于点E，以P为圆心，PE长为半径画圆，请判断AB与⊙P的位置关系并说明理由.

【解析】AB与⊙P相切.

例5 （2013·山东菏泽）如图11，BC是⊙O的直径，A是⊙O上一点，过点C作⊙O的切线，交BA的延长线于点D，取CD的中点E，AE的延长线与BC的延长线交于点P.试说明：AP是⊙O的切线.

【解析】如图12，由于A在圆上，那么我们可以连接OA，说明∠OAP=90°，即OA⊥AP，则AP是⊙O的切线.

理由：连接AC、AO，

∵BC是⊙O的直径，

∴∠BAC=90°，∠CAD=90°，

∵在△ADC中，∠CAD=90°，E为CD的中点，

∴AE=CE，∴∠EAC=∠ECA，

∵OA=OC，∴∠OCA=∠OAC，

∴∠EAC+∠OAC=∠ECA+∠OCA，即∠OAE=∠OCE.

∵CD是⊙O的切线，

∴OC⊥CD，即∠OCE=90°，

∴∠OAE=90°，即OA⊥AP且AP过半径OA外端A，

∴AP是⊙O的切线.

【点评】例4、例5都是考查圆的切线，但思路完全不同.例5：已知直线和圆的交点A，则连接圆心和交点，说明“垂直”即可；例4：没有直线和圆的交点，则要过圆心作此直线的垂线段，说明这条垂线段的长（即圆心到这条直线的距离d）等于这个圆的半径r.

变式4 （2015·辽宁大连）如图13，AB是⊙O的直径，点C、D在⊙O上，且AD平分∠CAB.过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F.试说明：EF与⊙O相切.

【解析】如图14，由于点D在⊙O上，要说明EF与⊙O相切，只要连接OD，说明OD⊥EF即可.

变式练习 （2015·江苏泰州）如图15，△ABC 中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F.试说明：DF是⊙O的切线.

圆是中心对称图形、轴对称图形，圆还具有绕圆心旋转任意角度都能与它自身重合的性质.利用圆的这些性质，可以得到本章很多的结论，本文重点研究了“圆周角定理”和“直线与圆的位置关系——相切”两个重要的结论，同学们只有熟练掌握了这些基本的性质，才能灵活运用它们解决圆的性质及其他知识的综合题.

（作者单位：江苏省常州市武进区湖塘实验中学）