从“用图”到“构图”

刘梅兰

小学阶段儿童的认知水平处于皮亚杰的“具体运算思维”阶段，其最大特点是思维离不开具体直观的支持。因而，儿童学习数学的过程，只有充分借助形象直观的教学手段，才能有效地帮助学生实现从直观到抽象的跨越。因此，在教学中我们要依托图形帮助学生学会“用图”，打好几何直观的基础，养成运用图形解决问题的意识，从而深入理解数学概念，提高解决问题的水平，发展几何直观能力。

一、“用图”——打好几何直观的基础

“用图”就是教师引导学生充分利用教材中提供的图，借助图，理解题意，分析数量关系，探索解题思路，提高分析和解决问题的能力。

（一）借助图理解数学概念

几何直观作为一种思维方式，是形象思维和抽象思维的中介，可以凸显数学概念的本质，有助于学生理解数学知识，提高数学素养。

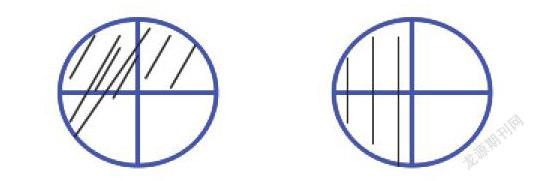
在教学苏教版五年级下册“真分数和假分数”一课中，认识是这节课的难点，因为、和都可以用一个单位“1”表示出来，但是至少要用两个单位“1”才能表示。教学中，笔者放手让学生同桌合作选择材料，分一分、涂一涂。并展示不同学生的不同表示方法。

第一种：用了两个圆，每个圆都平均分成了4份，第一个圆涂满，第二个圆涂1份。

第二种：用了两个圆，每个圆都平均分成了4份，第一个圆涂3份，第二个圆涂2份。

第三种：用了三个圆，每个圆都平均分成了4份，第一个圆涂2份，第二个圆涂2份，第三个圆涂1份。

引导学生在观察、比较的过程中抓住的本质属性：把单位“1”平均分成4份，表示这样的5份，大于1。有了涂色图形的支撑，学生很容易领会到这类分数的特征，掌握这类分数的本质属性。

在学生认识了之后，教师先引导学生说说其他像这样的分数，学生说出了分母不是4的假分数，说出了大于2的假分数等。接着，教师要求学生在教师提供的图形或数轴上表示出这些分数。这样的教学，扩大了假分数的外延，同时学生在图中表示出自己选的假分数时，又对假分数的内涵有了更深的理解和把握。

（二）重视表象和言语的转换

几何直观要求将抽象的数学语言与直观图形有机地结合起来，实现表象与言语的转换，促进学生的深入理解。

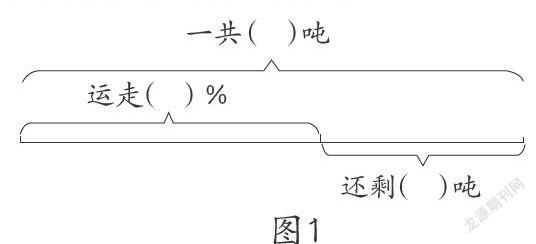
例如，苏教版六年级上册“百分数”单元，教学例10（马山粮库要往外地调运一批粮食，已经运走了60%，还剩48吨。这批粮食一共多少吨？）时，可以引导学生根据题意把书上的线段图（图1）填写完整，接着让学生根据线段图说说题意，并根据线段图分析数量关系，找到等量关系式：运走的吨数+剩下的吨数=总吨数。

先读题画图，再看图说题意，由图说“理”，通过这样的训练，可以提高学生的数学表达能力、几何直观能力和解决实际问题的能力。

（三）重视数学的直观洞察

随着学生数学知识的增长，数学学习水平的提高，我们应该为学生创造直观洞察的机会，提升学生几何直观能力的层次，更好地促进学生几何直观能力的发展。

例如，在教学苏教版五年级上册第七单元“解决问题的策略”例1（王大叔用22根1米的木条围一个长方形花圃，怎样围面积最大？）时，我们先让学生在理解题意的基础上用22根小棒围一围，进一步明确周长与小棒根数，小棒自身长度与长方形长、宽的关系。接着通过讨论明确要知道“怎样围面积最大”，就要先把所有的围法一一列举出来 ，再通过计算找出最佳方案。此时我们可以让学生在方格纸上将列举出来的所有长方形画出来（如图2），再引导学生观察、比较，找出规律。

于是，通过画图，学生理解了为什么当周长是22米时，长6米、宽5米的长方形面积最大。有的学生甚至能够发现随着长和宽的慢慢接近，面积的增加幅度在逐渐减小（图2中涂色部分为依次增加的面积）。这样的教学，在引导学生通过列举得出结论、解决问题之后，让学生画一画、想一想，借助几何直观使得学生在知其然的基础上知其所以然。诸如此类的例子，有助于学生养成良好的观察习惯，并不断积累直观理解、直观洞察的经验，感悟几何直观的作用，体会其价值，增强运用几何直观的意识。

二、“构图”——培养创造性思维

几何直观可以将抽象的问题具体化、复杂的问题简单化，从而帮助学生理解题意，探索解题思路，提高学生的分析问题、解决问题的能力。因此，对于学生而言，怎样根据题目的类型和特征构建出一个“图”显得至关重要。因此，随着学生年级的升高、数学题目难度的增加，我们要注重学生“构图”能力的培养。

（一）适度拓展，开阔眼界

我们在日常教学过程中要适时拓展几何直观的应用范围，强化学生几何直观的意识，培养其几何直观能力。

例如，苏教版五年级下册“3的倍数的特征”一课的教学，教材要求学生在百数表（见图3）中将3的倍数圈出来，发现从个位上看不出3的倍数的特征，接着通过在计数器上拨珠猜想来验证3的倍数的特征。

这样的教学，学生虽然能够发现3的倍数的特征，但是不理解为什么3的倍数，它的各位上数的和一定是3的倍数。如果出示图4，让学生将每个计数单位3个3个地涂一涂，就会发现1个十3个3个地涂剩下1个，几个十就会剩下几个；1个百3个3个地涂剩下1个，几个百也会剩下几个。因此，把百位、十位上剩下的小方块和个位上的小方块合起来，得到的块数是3的倍数，说明这个数就是3的倍数，反之，则说明这个数不是3的倍数。我们用直观的方法追本溯源，引导学生在操作活动中理解3的倍数的特征。借助方块图，有的学生甚至会发现，一个数各位上数的和除以3余几，这个数除以3也会余几。这样的教学，帮助学生理解知识的本质，拓展了学生的知识面，提高了学生的理解能力。

（二）借助想象，学会表征

联想和想象是拓展学生几何直观思维空间的主渠道，是发展学生几何直观能力的重要手段。

例如，在教学“圆的面积”一课时，我们先让学生通过数方格的方法算一算圆的面积大约是半径平方的多少倍。接着，让学生将圆平均分成16等份，拼成一个近似的平行四边形。再让学生在第一次操作的基础上想象：“如果把圆平均分成32份、64份，拼成的图形会有什么变化？”并用课件呈现出把圆平均分成32份、64份后拼成的图形，引导学生观察、比较。在此基础上，提问：如果无限细分下去，最终拼成的是什么图形？在图形直观的基础上想象、推理，渗透了极限的思想，培养了学生的空间想象能力。

（三）巧妙构图，灵活解题

在解决数学中的一些问题时，我们要巧妙构图，寻求它的几何表征。这样，对于问题的解决是有效的，既能实现问题直观的表达，又强调了对数学本质的认识。抓住了数学本质，就可以打开数学模式或形式化的遮掩，理清解题思路或找到解题方法，实现解题突破和解题优化。

例如，在完成练习题1+3+5+7+9+11+13+15+17

+19+21+……+99时，我们可以引导学生画图（图5）进行分析。

这样，学生借助构造的图形可以发现这样的规律：从1开始n个连续奇数的和等于n的平方。由此，可以很快算出1+3+5+7+9+11+13+15+17+19+21+……+99的得数就等于502，也就是2500。

本题的解决，一方面学生更加体会到几何直观的重要性，它不仅可以帮助我们找到解题的思路，而且降低了解题的难度；另一方面，学生构图的能力得到了锻炼，促进学生创造性思维的发展。

再如， 已知下图（图6）中阴影部分的面积是100平方厘米，求圆环的面积。

我们知道，这道题中两个圆的半径都是未知的，所以学生常常感觉无从下手。我们可以引导学生将大圆半径标为R，将小圆半径标为r。那么已知条件“阴影部分的面积是100平方厘米”，就可以表示为：R2+r2=100。而要求的是圆环的面积，也就是求π（R2+r2）等于多少。我们将R2+r2=100和π（R2+r2）写在一起，学生一下就明白，要求圆环的面积，只要用π乘100就可以了。

这些用字母、符号、文字表示的等量关系式虽然是数量关系的抽象表达，相对于文字的抽象来讲，却是一种“直观”的表达，有助于学生理解、分析问题。

总之，“几何直观”在整个数学学习过程中都发挥着重要的作用，在教学中我们要充分学习、领会“几何直观”的深刻内涵，引导学生 “用图”，为几何直观能力的形成打下坚实的基础，进而“构图”，灵活运用几何直观的方法，创造性地解决实际问题，提高学生的数学素养。

（江苏省南京晓庄学院附属小学 210038）