以不变应万变

生活中有许多美妙的图形，它们都是由简单的图形构成.而我们在解决有关图形问题时，应该抓住图形在变化的过程中，不变的解决问题的基本方法，以不变应万变，一通百通.

一、“图形变化，结论不变”型问题

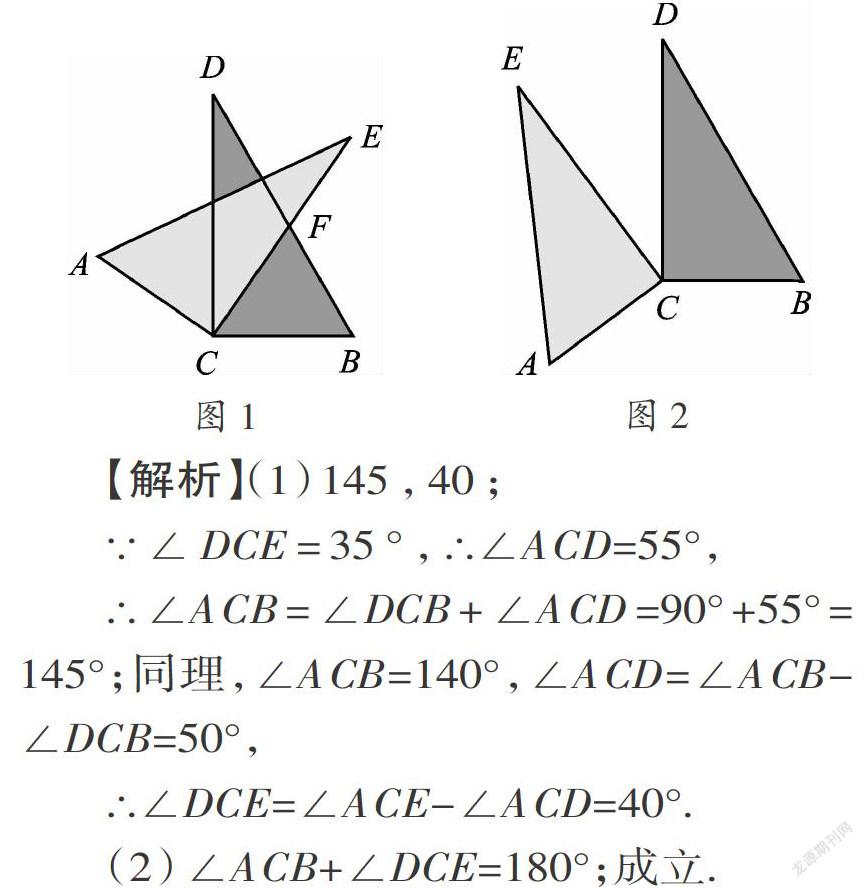
例1.小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起，若保持△BCD不动，将△ACE绕直角顶点C旋转.

说明：在解决有些图形的问题时，我们经历从特殊到一般的过程，同时伴随着图形的变化，然而，我们应该抓住与此相关的不变的知识点，类似的解决问题的方法，从而以不变应万变。

二、“图形变化，方法不变”型问题

例2.已知：O为直线AB上的一点，OC⊥OE于点O，射线OF平分∠AOE.

（1）如图1，判断∠COF和∠BOE之间的数量关系？并说明理由；

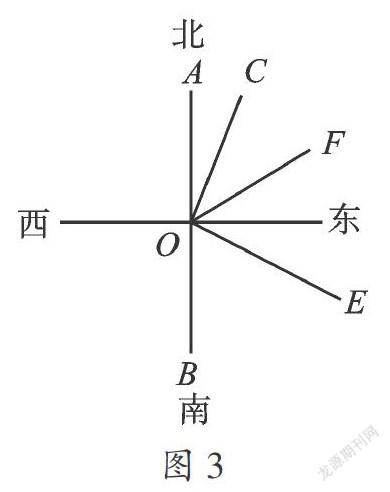
（2）若将∠COE绕点O旋转至图2的位置，试问（1）中∠COF和∠BOE之间的数量关系是否发生变化？若不发生变化，请你加以证明，若发生变化，请你说明理由；

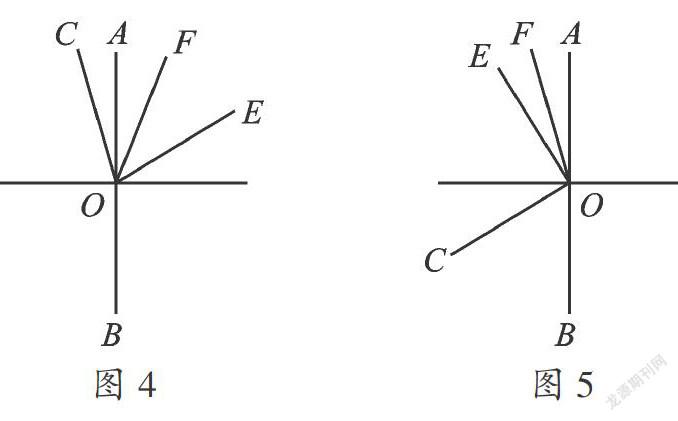
（3）若将∠COE绕点O旋转至图3的位置，继续探究∠COF和∠BOE之间的数量关系，并加以证明.

说明：图形虽然在变化，问题的结论有可能也在变化，但解决问题的方法没有改变，我们只要始终结合所学的垂直、角平分线等知识，角的和差表示，同样可以解决问题。

只要我们充分掌握基本知识、基本技能，灵活应用，以不变应万变，学号初中几何。