厘清关系才能得心应手

王晓玲

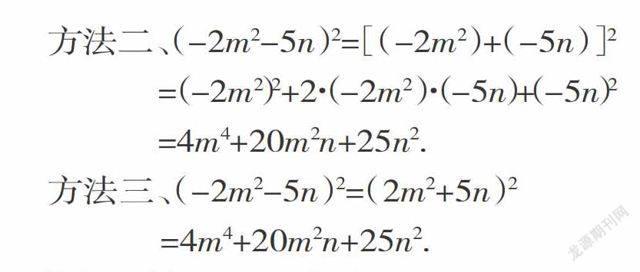
因式分解与整式乘法是一对“孪生兄弟”，它们可以互逆变形、相互转化. 实践证明，只有厘清它们之间的关系，做到正反灵活运用，才能真正认清它们之间的内在联系. 下面对这部分内容的难点进行剖析，希望对大家的学习有所帮助.

一、 整式乘法

【点评】三种计算方法中，以方法一最为基础，其实质在于“往前乘，莫回头”，它是多项式乘多项式的基本方法，必须掌握. 方法二、方法三均运用了平方差公式，起到了简化运算的作用，也需熟练掌握.

【点评】平方差公式中的a、b可以是单项式，也可以是多项式，如果是多项式，要注意观察，善于求同寻异，找准“相同项”“相反项”或“相同整体”“相反整体”，培养自己处理问题的整体意识.

【点评】完全平方公式的运用要有一定的灵活性，切不可生搬硬套，虽然上述三种方法均运用了完全平方公式进行计算，但运用方法一和方法二要有一定的整体意识，且符号容易出错，方法三先对符号做了处理，问题就变得简单多了.

二、 因式分解

【点评】因式分解的结果是几个整式的积的形式，千万不能将因式分解和整式的乘法混淆，走“回头路”. 使用平方差公式分解因式时，必须认准公式a2-b2=（a+b）（a-b）中的“a”与“b”. 公式中的a、b可以是单项式，也可以是多项式. 将多项式因式分解时，如果首项系数是负数，一般都要通过重新调整顺序或提取负号，将首项系数转化为正数.

（作者单位：江苏省东台市唐洋镇中学）