第11讲 “动手操作问题”复习精讲
2015-09-10刘顿
刘顿


专题精讲
所谓“操作”,是指人用手活动的一种行为,也是一种技能,含义很广泛.一般是指劳动、劳作,或者按照一定的规范和要领操纵动作,数学中的操作题一般是需要对数的设置或对图形的变换、剪拼等,由于此类试题既可以有效地巩固数学知识,又可以提高同学们的动手能力,所以中考中频频“上演”此类问题.
重点题型例析
一、对数的操作
例1(2014.娄底)按照下面所示的操作步骤,若输入值为3,则输出的值为________.
分析:由操作程序可知,32=9<10,来确定运算程序,按“加上2”再“乘以5”输出.
解:由32=9<10.可知应选择“是”的运算程序计算,(9+2)x5=55,即输出的值为55.
反思:解此类题时,应正确地选择运算操作程序,避免:①错选“否”的运算程序;②错把10作为一个结果参与运算;③不按每一步的结果得数进行计算,如32+2x5=19.
二、对式的操作
例2 (2014.台州)有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:
则第n次的运算结果=________.(用含字母x和n的代数式表示)
分析:要探究操作的第n次运算结果,可分别将第2、3、4次的分式计算、化简,再将化简后的分式列表分析、发现规律.
解:依题意,可列表如表1.
四、阅读与操作
例4 (2014.山西)阅读下列材料,按要求完成相应的任务.
几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形——筝形,所谓筝形,它的形状与我们生活中风筝的骨架相似.
定义:两组邻边分别相等的四边形,称之为筝形,如图4,四边形∠ABCD是筝形,其中AB=AD,CB=CD.
判定:①两组邻边分别相等的四边形是筝形.②有一条对角线垂直平分另一条对角线的四边形是筝形.
显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点.如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)清说出筝形和菱形的相同点和不同点各两条.
(2)请仿照如图5的画法,在如图6所示的8x8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:①顶点都在格点上;②所设计的图案既是轴对称图形又是中心对称图形;③将新图案中的四个筝形都涂上阴影(建议用一系列平行斜线表示阴影).
分析:(1)利用菱形的性质以及结合图形得出筝形的性质分别得出异同点即可.(2)利用轴对称图形和中心对称图形的定义结合题意得出答案,显然答案不唯一.
解:(1)相同点:①两组邻边分别相等;②有一组对角相等;③有一条对角线垂直平分另一条对角线:④有一条对角线平分一组对角;⑤都是轴对称图形;⑥面积等于对角线乘积的一半.不同点:①菱形的对角线互相平分,筝形的对角线不互相平分;②菱形的四边都相等,筝形只有两组邻边分别相等;③菱形的两组对边分别平行,筝形的对边不平行;④菱形的两组对角分别相等,筝形只有一组对角相等;⑤菱形的邻角互补,筝形的邻角不互补;⑥菱形既是轴对称图形又是中心对称图形,筝形是轴对称图形不是中心对称图形.(2)答案不唯一,如图7所示中的任意一种情形.
反思:求解此类问题时,一定要充分借助网格特点进行作图,解题的关键是正确理解平移、轴对称、旋转以及中心对称图形、轴对称图形的意义.
五、裁剪操作
例5 (2014.宁波)用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图8所示的两种方法裁剪(裁剪后边角不再利用).
A方法:剪6个侧面:B方法:剪4个侧面和5个底面,
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用含x的代数式分别表示裁剪出的侧面和底面个数.
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
分析:(1)根据一张硬纸板用A方法剪6个侧面 ,B
六、对图形的分割操作
例6 (2014.漳州)如图9,△ABC中,AB=AC,∠A=36。,称满足此条件的三角形为黄金等腰三角形.请完成以下操作(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC):
(1)在图9中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是______度和______度.
(2)在图10中画2条线段,使图中有4个等腰三角形.
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有______个等腰三角形,其中有______个黄金等腰三角形.
分析:(1)利用等腰三角形的性质以及∠A的度数,进而得出这两个等腰三角形的顶角度数.(2)利用(1)中思路进而得出符合题意的图形.(3)利用画1条线段可得到2个等腰三角形,画两条线段可得到4个等腰三角形,画3条线段可得到6个等腰三角形,进而得出规律求出答案.
解:(1)如图9所示AB=AC,∠A =36。,故当AE=BE时,∠A= ∠ABE=36。,则∠AEB=108。,则∠EBC=36。,故这两个等腰三角形的顶角度数分别是108度和36度.
(2)画法不唯一,如图10所示,四个等腰三角形分别是:△ABE,△BCE,△BEF,△CEF
(3)如图11.画1条线段可得到两个等腰三角形,画两条线段可得到4个等腰三角形,画3条线段可得到6个等腰三角形,…,在△ABC中画n条线段,则图中有2n个等腰三角形,其中有n个黄金等腰三角形.
反思:本题既是一道操作题,又是一道问题的探究题,求解时应注意作图技巧,灵活运用等腰三角形的性质,其中探究出分割图形的规律是解题关键.另外,在(2)中当画出线段BE时,余下的也可以过C作∠C的平分线交BE于点F
七、折叠操作
例7 (2014 临沂)对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开,
第二步:再一次折叠,使点A落在MN上的点A’处,并使折痕经过点B,得到折痕BE,同时,得到线段BA’,EA’,展开,如图12.
第三步:再沿EA’所在的直线折叠,点B落在AD上的点B'处,得到折痕EF,同时得到线段B’F,展开,如图13.
(1)证明:∠A BE=300.
(2)证明:四边形BFB’E为菱形.
分析:(1)根据点M是AB的中点判断出A’是EF的中点,然后判断出BA'垂直平分EF,根据线段垂直平分线上的点到两端点的距离相等可得BE=BF,再根据等腰三角形“三线合一”的性质可得∠A’BE=∠A 'BF,根据翻折的性质可得∠ABE= ∠A 'BE,然后根据矩形的四个角都是直角计算即可得证.(2)根据翻折变换的性质可得BE=B'E,BF=B'F,然后得出BE=B'E=B'F=BF,再根据四条边都相等的四边形是菱形证明.
解:(1)由对折AD与BC重合,折痕是MN,故点M是AB的中点,故A’是EF的中点,因∠BA’E= ∠A =90。,故BA’垂直平分EF,故BE=BF,故∠A' BE= ∠A 'BF,由翻折的性质,∠ABE=∠A'BE,故∠ABE= ∠A 'BE=∠A,BF,故∠ABE()×90。=30。.
(2)沿EA’所在的直线折叠,点B落在AD上的点B’处,故BE=B'E,BF=B'F因BE=BF,故BE=B'E=B'F=BF,故四边形BFB'E为菱形.
反思:本题通过操作,意在考查矩形、菱形、线段垂直平分线等知识.解答折叠问题的一般思路:分清折叠前后的对应边、对应角、对称轴,利用对称轴是对应点所连线段的垂直平分线寻找相等的线段或角,进行相关的计算或证明.
中考命题预测
1.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线l,使截得的三角形与原三角形相似,这样的直线l有____条.
2.如图14,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动____格.
3.如图15,将一副七巧板拼成一只小动物,则∠AOB=____.
4.如图16,小亮拿一张矩形纸如图16 (1),沿虚线对折一次得图16 (2),将对角两顶点重合折叠得图16(3).按图16(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是().
A.都是等腰梯形
B.都是等边三角形
C.两个直角三角形,一个等腰三角形
D.两个直角三角形,一个等腰梯形
5.在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图17):
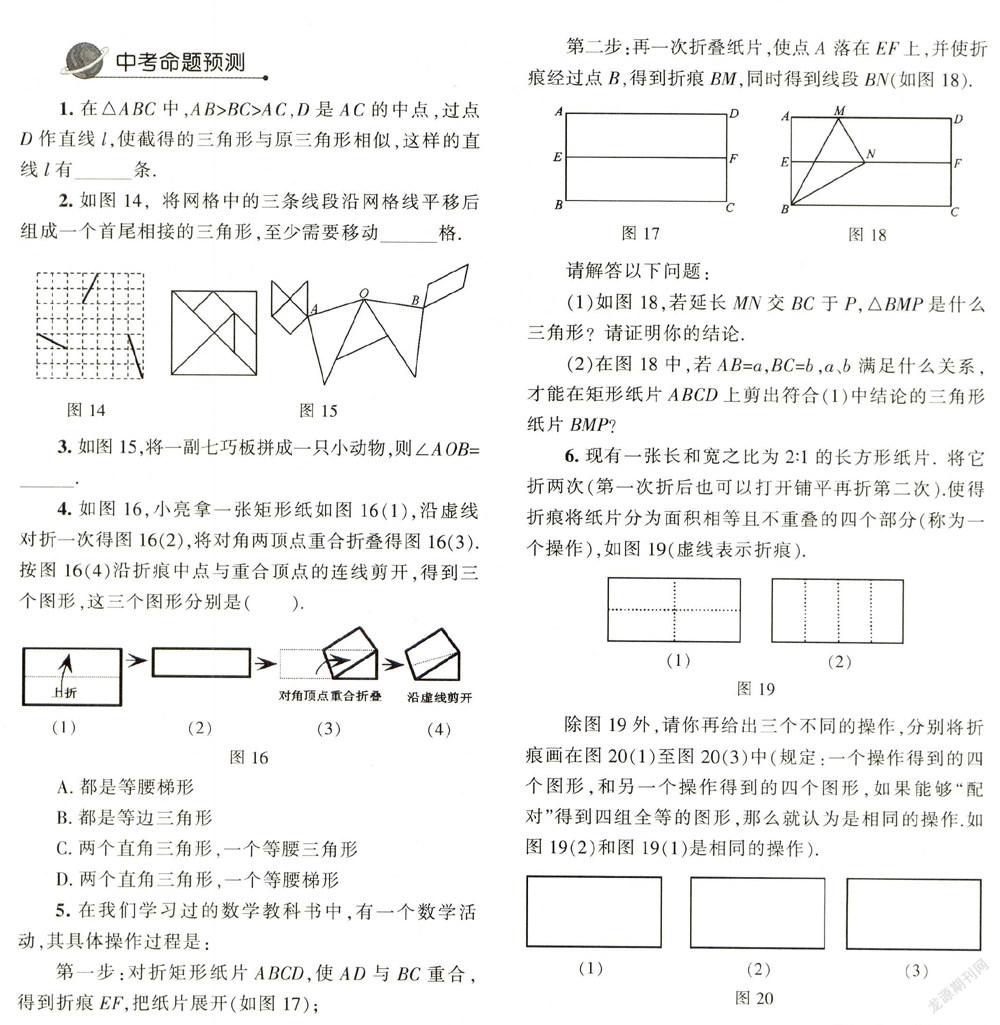
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图l8).
请解答以下问题:
(1)如图18,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论.
(2)在图18中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出{符合(1)中结论的三角形纸片BMP?
6.现有一张长和宽之比为2:1的长方形纸片,将它折两次(第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图19(虚线表示折痕).
除图19外,请你再给出三个不同的操作,分别将折痕画在图20(1)至图20(3)中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图19(2)和图19(1)是相同的操作).(上接第26页)点同时从点P 出发,点A以5 cm/s的速度沿射线PM方向运动,点B以4 cm/s的速度沿射线PN方向运动.设运动时问为t(s).
(1)求PQ的长.
(2)当t为何值时,直线AB与00相切?
3.如图8,在平行四边形ABCD中.AD=4 cm,∠A=60。,BD ⊥AD.一动点P从A出发,以每秒l cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2 s时,设直线PM与AD相交于点E,求△APE的面积.
(2)当点P运动2s时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒l cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动.过Q作直线QN,使QN∥PM.设点Q运动的时问为t(0≤t≤10)s,直线PM与QN截平行四边形ABCD所得图形的面积为S( cm2).求S关于£的函数关系式.
