实验设计方法在氮气泡沫调剖优化设计中的应用

万单静，万单梁，黄威，郭志文，冯海峰（.中原油田分公司内蒙采油事业部，河南濮阳　45700；.中原油田分公司采油一厂，河南濮阳　4577）

实验设计方法在氮气泡沫调剖优化设计中的应用

万单静1，万单梁2，黄威2，郭志文2，冯海峰2
（1.中原油田分公司内蒙采油事业部，河南濮阳457001；2.中原油田分公司采油一厂，河南濮阳457172）

在进行氮气泡沫调剖的设计中，影响氮气泡沫调剖效果的主要因素有注入时机、气液比、表面活性剂浓度、注入段塞尺寸等。本文在单因素分析法确定各因素最佳取值范围基础上，利用优化设计软件对影响氮气泡沫调剖的参数进行了优化设计，在此基础上进一步回归了增油量公式，经与数值模拟软件计算结果对比，公式的平均相对误差为1.15％。关键词：实验设计；数值模拟；多元回归；方差分析

实验设计（design of experiment，DOE）是一种确定多因素交互作用的设计方法，可以用于任何有可量度的输入输出过程，DOE提出了一种通过优化设计选择参数值的计算方案［1］，用最少的运算次数定量评价各种不确定性因素的影响，并能得到目标函数的计算公式，并通过把目标函数公式作为代理模型来代替原来复杂的计算模型，从而达到在基本不影响计算精度的前提下大大简化计算，提交劳动生产率的目的。该方法在国外［2-8］被广泛的运用到油气田开发中，已取得了很好的效果，国内学者［9］也有把实验设计方法运用到气井产能评价中取得成功的案例。

实验设计及其优化是当代科学研究、工程技术与管理中得到广泛应用的一门学科，也是数理统计的应用方法之一。在农业、冶金、材料、化工等多个行业都得到了广泛的应用与发展，并取得了显著的成绩和非常可观的经济效益。综合运用DOE实验设计软件和油藏数值模拟方法可以得到注聚井在不同注入参数组合下的增油量，从而进行调剖优化设计。

1　利用实验设计方法优化影响氮气泡沫调剖的参数

涉及到多因素时，各因素不仅各自独立起作用，而且还彼此影响，相互结合起来对目标变量起作用，即不仅各因素水平改变时对试验指标有影响，而且各因素的联合搭配对试验指标也有影响。因此必须在单因素分析［10］的基础上，利用实验设计方法进行多因素分析。

本文以西达里亚油田为例，在单因素分析的基础上，选定注入时机为77％，将主段塞分为三小段塞间隔30 d注入。根据油田实际情况利用实验设计方法（DOE）选取表面活性剂质量和浓度、气液比、段塞PV数作为优化参数，选择增油量作为目标函数，段塞组合的基本注入参数（见表1），基于单因素分析法得到的的各变量范围确定了优化设计时各参数的取值范围（见表2）。三变量三水平共27种组合，在DOE软件中通过选用高斯方法可以获取13种典型的方案组合，不同组合方案，模拟累计增油量和模拟截至时含水率下降值（见表3）。

表1 基本注入参数Table1 basic injection parameter

表2试验设计中的变量取值范围Table2 values of a variable in DOE

由表3可以看出方案6的增油量最高，即为方案6的调剖效果最好，此时主段塞表面活性剂质量浓度为0.75％，气液比为1.5：1，注入PV数为0.15 PV。因此在考虑多因素交互作用时，并不是某个变量值越高越好，必须利用试验设计方法得到多个组合方案后再从中进行优选。

图1，图2表明了，刚开始注气时进入地层的氮气对地层平衡产生了影响使得含水率出现波动，此时生成的泡沫质量一般，气体上覆至高构造部位后增加了油藏内部的弹性能，使得产水量增加，含水率上升。随着注气的继续，一部分气体随液产出，地层条件逐步趋于稳定，氮气与表面活性剂溶液混合形成的高质量氮气泡沫开始发挥主导作用，调剖封堵高渗透层使井组含水率下降，在停止注剂一段时间后，泡沫逐渐破灭，泡沫质量降低，调剖效果开始减弱，使得井组含水率开始缓慢上升，这些因素使得含水率曲线呈一“V”字形。

2　增油量公式回归

利用DOE正交试验设计软件对表3中不同参数组合得到的增油量计算结果进行回归分析，得到增油量计算公式为：

Q=-692.431 5+1 425.710 5×X（1）+8 849.346×X（2）-

5 132.952 5×X（3）-249.292×X（1）×X（2）-1 915.98×

X（1）×X（3）-4 502.28×X（2）×X（3）-747.078×

X（1）2-2 742.140 5×X（2）2+21 174.05×X（3）2（1）

数值模拟结果和公式回归公式计算结果关系曲线（见图3），数模结果和公式计算结果对比表（见表4），从图3表4中可以看出，二者很接近。计算结果最大相对误差2.387％，13个方案平均相对误差1.154％，表明回归得到的增油量计算公式精确度较高，实用性较强。再次改变注入参数时不必利用CMG软件进行模拟计算，可直接通过公式计算，这将节省大量工作时间提高工作效率。

图1　不同试验设计方案累计产油Figure1 cumulative oil of different DOE case

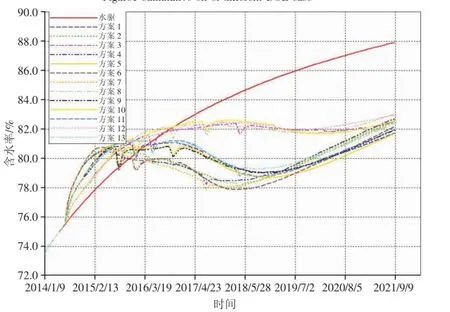
图2　不同试验设计方案含水率Figure2 water cut of different DOE case

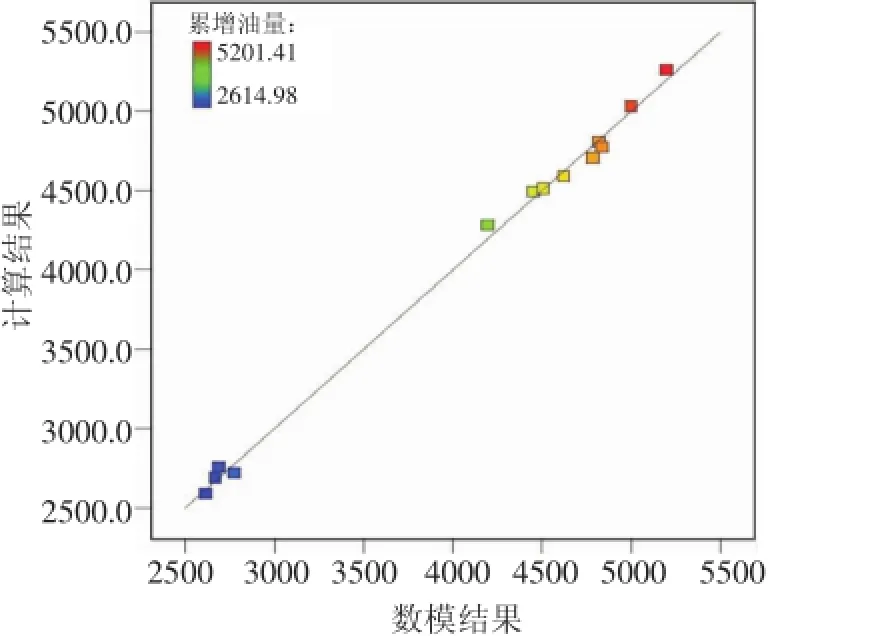
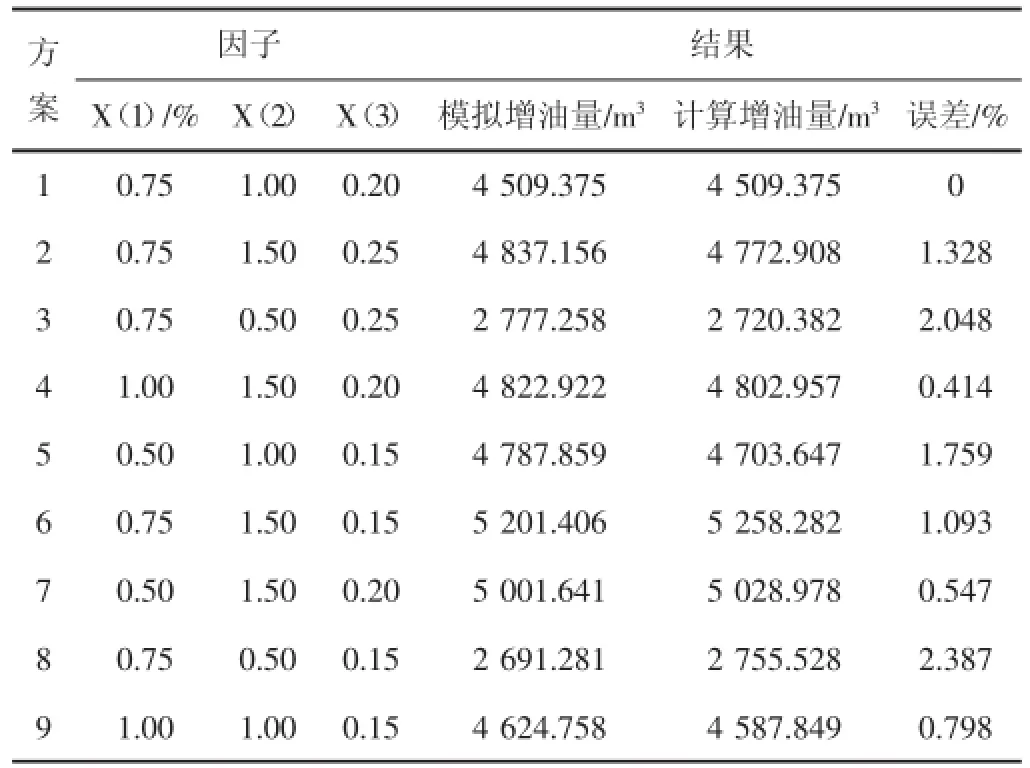
表4　数模结果和公式计算结果对比表Table4 the comparison between numerical simulation result and calculation result

表4　数模结果和公式计算结果对比表（续表）Table4 the comparison between numerical simulation result and calculation result（Continue table）

3　参数显著性分析

方差分析法是利用数理统计中F检验法判断各因素对试验指标影响的显著程度和可信程度。利用F分布表确定的临界值，通过比较计算出各因素F值与临界F值，判定各因素对评价指标的影响是否显著：大于临界值时影响显著，小于临界值时影响不显著。进而确定影响评价指标参数的主次顺序。

利用DOE试验设计软件对注入参数进行多因素方差分析，可以快速的得到各因素的F值。检验水平α取为0.05时，临界值F为10.13。因此可以看出表面活性剂质量浓度对累增油量有影响但不显著，气液比对累增油量影响高度显著，注入段塞尺寸对累增油量影响但显著性不大。根据F值的大小，判断出各注入参数对累增油影响的程度大小依次为气液比，注入段塞尺寸和表面活性剂质量浓度。

表5　多因素方差分析表Table5 factorial analysis of variance table

4　结论及建议

（1）运用实验设计对影响氮气泡沫调剖的多参数进行优化设计，在考虑多因素交互作用时，并不是某个变量值越高越好，必须利用实验设计方法得到多个组合方案后再从中进行优选。

（2）优化设计回归的增油量方程有很高的精度，通过数值模拟结果和回归公式计算结果对比，优化设计所得到的方程平均相对误差为1.15％。再次改变注入参数时不必利用CMG软件进行模拟计算，可直接通过公式计算，这将节省大量工作时间提高工作效率。

（3）实验设计和响应面方法可以克服传统方法无法确定因素间交互作用的局限性，优化油田开发方案。

［1］Yelen B，Castellini A，et al.A Comparison study on Experimental Design and Response Surface Methodologies［C］.SPE93347，2005.

［2］Gupta R，Collinson R，Smith G C，et al.History Matching of FieldProductionUsingDesignofExperiment［C］. SPE115685，2008.

［3］Olaoluwa A，Odusote O，Novakovic D，et al.Improving Production Forecasts Through the Application of Design of Experiment and Probabilistic Analysis，A Case Study from Chevron Nigeria［C］.SPE128605，2009.

［4］Thomes S，Bertrand C，Nicolas L，et al.Using Experimental Design Assissted History Matching Tools and Bayesian Framework to Get Probabilistic Production Forecasts［C］. SPE113498，2008.

［5］Zang L G，Graf G，Al-kinani A，et al.Proxy Modeling in Production Optimization［C］.SPE100131，2006.

［6］Guilherme D A.Use of Proxy Models in the Selection of Production Strategy and Economic Evaluation of petroleum Fields［C］.SPE129512，2009.

［7］Carreras P E，Johnson S G，Turner S E，Tahiti：Assessment of Uncertainty in a Deepwater Reservoir Using Design of Experiments［C］.SPE102988，2006.

［8］Amudo C，Graf T，Harris N R，er al.Experiment Design and Response Surfance Modela as a Basis for Stochastic History Match-a Niger Delta Experience［C］.ISTC12665，2008.

［9］刘志森，Kamy Sepehrnoori，喻高明，等.利用优化设计和节点分析方法确定吐哈丘东气田气井产能方程［J］.石油天然气学报，2011，33（12）：124-127.

［10］马成良，张海军，李素平.现代试验设计优化方法及应用［M］.郑州大学出版社，2007：1-3.

The application of DOE method in the optimal design of N2foaming profile control

WAN Danjing1，WAN Danliang2，HUANG Wei2，GUO Zhiwen2，FENG Haifeng2
（1.Zhongyuan Oilfield Branch of Inner Mongolia Production Division，Puyang Henan 457001，China；2.Oil Production Plant 1 of Zhongyuan Oilfield Branch，Puyang Henan 457172，China）

During doing the N2foaming profile control design，the major factors affecting the N2foaming profile control are injection time，gas liquid ratio，the concentration of surface active agent，the size of injeted slug etc.In this paper，for the parameters affecting on the N2foaming profile control，the optimal design is conducted by taking advantage of the optimal design software.Which is based on the optimum value range of various factors determined by the sigle factor analysis method，and then.Oil increment formula has been made further regression.Compared with the results through numerical simulation software.The average relative error of this formula is1.15 percent.

design of experiment；numerical simulation；multiple regression；analysis of variance

10.3969/j.issn.1673-5285.2015.01.016

TE357.7

A

1673-5285（2015）01-0058-04

2014－10－30

2014－12－15

万单静，女（1976-），西安石油大学石油工程专业，主要从事油气田开发工作，邮箱：helil_hi@126.com。