活性炭对废水中表面活性剂的吸附研究

张新

摘要：以活性炭为吸附剂，研究其对表面活性剂溶液的吸附作用。利用Langmuir、Freundlich和Dubinin-Radushkevich等温吸附模型对数据进行拟合，发现Langmuir模型拟合较好，并且吸附过程是物理过程。利用准一级、准二级动力学和颗粒内扩散模型检验动力学吸附数据，计算和比较这些动力学模型的吸附速率常数，发现用准二级动力学模型能最佳地描述吸附动力学。利用Thomas、Yoon-Nelson和Adams-Bohart模型对固定床吸附数据进行拟合，发现Thomas和Yoon-Nelson模型拟合较好.

关键词：吸附模型； 表面活性剂； 活性炭

中图分类号：X53 文献标识码：A 文章编号：0439-8114（2015）15-3642-04

DOI：10.14088/j.cnki.issn0439-8114.2015.15.014

Abstract： Removal of surfactant from aqueous solutions by activated carbon was investigated.As for the batch adsorptions， the experimental data were analyzed by Langmuir， Freundlich and Dubinin-Radushkevich isotherm model. The experiment results indicated that the adsorption data were fitted well with Langmuir isotherm model. The Dubinin-Radushkevich isotherm model indicates adsorption process is a physical adsorption. The kinetics of adsorption process data was examined using the pseudo-first-order， pseudo-second-order kinetics and the intra-particle diffusion models.The rate constants of adsorption for all these kinetics models were calculated and compared.The adsorption kinetics was best described by the pseudo-second-order model.As for the fixed-bed adsorptions， the experimental data were analyzed by Thomas、Yoon-Nelson and Adams-Bohart model. The experiment results indicated that the adsorption data were fitted well with Yoon-Nelson and Adams-Bohart model.

Key words： adsorption models； surfactant； activated carbon

土壤洗涤是一种异位土壤修复技术，可应用于土壤重金属和有机污染修复，该技术始于欧洲20世纪80年代，美国从20世纪80年代末期开始应用于土壤修复，在中国目前基本上还处于实验室阶段[1]。该技术通常需要加入表面活性剂等添加剂来增强去除效果，洗涤后可以去除90%～99%的挥发性有机物和40%～90%的半挥发性的有机物[2，3]。通常认为添加非离子型表面活性剂的清洗效果最好，其中使用较多的是Triton X-100[4-6]。在土壤洗涤时，为达到一定的修复效果，需要投加较高浓度的表面活性剂，这样产生的土壤洗涤液中表面活性剂浓度也较高，必须加以处理后才能排放。

本研究使用活性炭对含表面活性剂的废水进行吸附处理，分别进行静态吸附、动力学吸附和固定床吸附试验，并使用多种模型对吸附数据进行拟合，旨在为含表面活性剂废水处理提供理论指导和技术支持。

1 材料与方法

Triton X-100购于中国百灵威科技有限公司，活性炭购于中国西陇化工股份有限公司。活性炭比表面积为718.2 m2/g、孔容为0.845 cm3/g、孔隙分布0.200～2.000 nm、平均孔径是0.845 nm、微孔体积是0.397 cm3/g、中孔体积是0.206 cm3/g、大孔体积是0.242 cm3/g。

静态吸附试验：配制浓度为5 g/L的TX100溶液，逐级稀释至4.00、3.00、2.00、1.00、0.50和0.15 g/L。在150 mL锥形瓶中加入100 mL的TX100系列浓度溶液，然后加入1 g/L活性炭，使用封口膜封口，在转速为120 r/min的恒温振荡箱（25±0.5℃）中振荡48 h。

动力学试验：使用浓度为5 g/L的TX100溶液，吸附条件同静态吸附试验，分别在10、20、30、40、60、120、180、240、480、600、900、1 080和1 440 min时将样品取出。

固定床试验：使用有机玻璃柱为吸附柱，其高20 cm，柱内径2.5 cm，内填充活性炭，TX100浓度为5 g/L，流速为20 mL/min，分别取活性炭柱高为7.0、10.8和14.7 cm，溶液从上往下流动，每隔15 min取样。吸附后使用离心机以4 500 r/min离心10 min，用玻璃注射器取上清液经PTFE过滤头注射至2 mL进样瓶中。使用DionexU3000的HPLC检测，色谱柱为Agilent PAH柱（250×4.6 mm），流动相比例为乙腈∶水=85∶15，柱温30 ℃，流速为1 mL/min，检测UV波长为230 nm。

2 结果与分析

2.1 吸附等温线

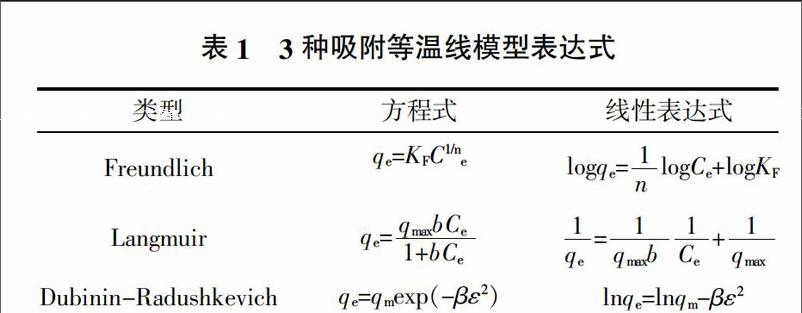
吸附等温线是指在一定温度下溶质分子在两相界面上发生的吸附过程达到平衡时在两相中浓度之间的关系曲线，是工业设计的基本依据。吸附等温线的类型很多，适用于不同的条件。Langmuir模型是根据理论推导出的第一个吸附方程式，其出发点是吸附和解吸速率是相同的，分子只能在吸附剂的自由表面上才会被吸附并形成单分子层，被吸附分子之间没有相互作用力[7]。Freundlich模型是一个经验方程，其特征是吸附位非均匀分布，吸附能不同，多用于描述非均质表面的单分子层吸附行为[8]。该吸附方程式简单，计算方便，应用广泛。但式中的常数没有明确的物理意义，不能说明吸附作用的机理。Dubinin-Radushkevich 模型假定吸附剂表面是不均匀的，吸附是吸附质填充吸附剂孔的过程[9]，该模型可以判断吸附是物理过程（E0<8 kJ/mol）、离子交换过程（8～16 kJ/mol）还是化学过程（E0 >16 kJ/mol）。当然也不能使用该模型判定一个吸附过程，即不能认为某一吸附只有化学吸附而没有物理吸附，该模型通常判别一个吸附过程是以哪种性质的吸附为主。这3种吸附等温线的表达式列于表1中。

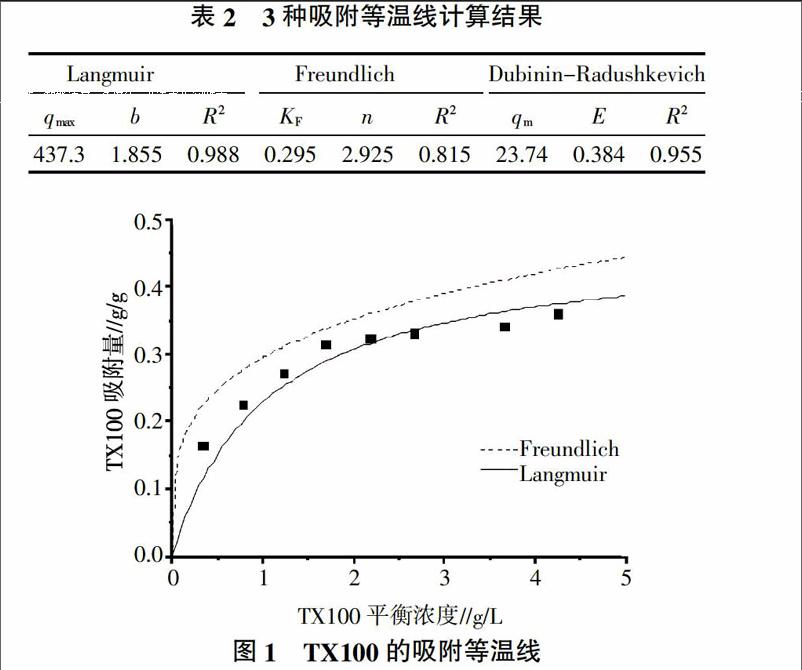
活性炭对TX100的计算结果如表2所示，吸附结果如图1所示。在一些研究中，非离子型的表面活性剂在其浓度超过CMC（临界胶束浓度）时，吸附特征是先形成单分子层，然后是表面积聚形成多层吸附结构[9-11]。而在本研究中，Langmuir模型的拟合效果比Freundlich模型更好，这与其他类似研究结论相一致[12-14]。可以设想TX100只是形成单分层而没有进一步的吸附，也就是说，TX100覆盖在活性炭的表面，而活性炭的内部孔隙没有起到主要作用。吸附过程的性质使用Dubinin-Radushkevich模型来判断，由表2知，E值<8 kJ/mol，这说明吸附过程是一种物理过程，这与前人研究结论一致。

2.2 吸附动力学

吸附动力学是研究各种因素对化学反应速率影响的规律，研究化学反应过程经历的具体步骤即所谓反应机理。准一级动力学模型的反应速度与一个反应物浓度成正比，应用时需要选取一个吸附平衡点[15]。一般情况下，准一级吸附动力学方程在全部吸附时间范围内的相关性并不是很好，通常只适用于吸附的初始阶段。准二级动力学模型的反应速度与两个反应物浓度成正比，基于假定吸附速率受化学吸附机理的控制，这种化学吸附涉及到吸附剂与吸附质之间的电子共用或电子转移[16]。内扩散模型假设液膜扩散阻力可以忽略或者是液膜扩散阻力只有在吸附的初始阶段的很短时间内起作用[17]，扩散方向是随机的、吸附质浓度不随颗粒位置改变且内扩散系数为常数，不随吸附时间和吸附位置的变化而变化。如果吸附动力学曲线都不经过原点，说明内扩散不是控制吸附过程的惟一步骤。Elovich模型考虑到真实吸附过程中随着吸附过程的进行，吸附和解吸活化能随吸附剂表面覆盖而线性变化的情况[18]。如果应用时不忽略解吸速率的影响，存在表面覆盖率随时间的变量，则方程式没有解析解，只有数值解。这4种吸附动力学模型的表达式列于表3。

图2是活性炭对TX100溶液吸附量随时间的变化，表4是使用模型后的拟合结果。准二阶动力学方程的R2值要高，而且吸附计算值接近试验值826.63 mg/g，故此方程的拟合效果好，说明表面活性剂的吸附满足准二阶动力学方程。从内扩散模型的数据来看，其C值是一个正值，说明吸附过程受到了表面扩散所控制。

2.3 固定床吸附模型

动态吸附柱的工作过程可用穿透曲线来表示，其中纵坐标为出水中吸附质浓度或出水与进水浓度比、横坐标为吸附时间。为模拟和预测动态柱内的吸附行为和规律，基于各种假设提出多种模型。Thomas模型假设溶液呈活塞流形态，通常用来描述吸附柱的动态吸附曲线[19]，并能计算出吸附柱的饱和吸附容量与吸附速率常数。Yoon-Nelson模型是一个半经验模型，该模型拟合时不需要考虑吸附流速和吸附剂用量[20]，所需已知参数较少，形式简单，得到的值可用于比较吸附速率。Adams-Bohart模型是描述吸附时间和柱高的关系，可用于计算吸附剂的吸附能力和吸附传质速率[21]。常见的固定床吸附模型表达式列于表5。

当流速为20 mL/min，TX100浓度为5 g/L，活性炭柱高为14.7 cm时，TX100的穿透曲线如图3所示，模型计算结果列于表6。随着柱高的增加，TX100的穿透时间延长，对应于7.0、10.8和14.7 cm，TX100穿透90%的时间分别是90、105和180 min。柱高增加，可利用活性炭吸附面积增大，则活性炭柱饱和时间缩短，使用时间加长，吸附容量也仍能增大。表现于Tomas模型，随着活性炭用量的增加，KTh和qe随之增加，这与实际吸附过程中得到的吸附的变化趋势相一致。表现于Adams-Bohart模型，活性炭用量大，则传质系数加大，说明吸附过程主要受到外部扩散所影响，由于在数据拟合过程中得到的相关系数相对较低，因此该模型对此过程的应用有一定的限制。表现于Yoon-Nelson模型，随着活性炭用量的增加，达到一半吸附量的时间自然会增加，KYN值也相应增加，从相关系数来看，该模型拟合效果较好，且达到一半吸附量的时间计算值与实测值较为接近，其较好地模拟了穿透行为。

3 小结与讨论

活性炭对表面活性剂的静态吸附符合Langmuir模型，这表示TX100在活性炭表面形成单分子层。从Dubinin-Radushkevich模型计算得到的E值<8 kJ/mol，说明吸附过程是物理过程。动力学吸附数据符合准二阶动力学方程。Thomas模型和Yoon-Nelson模型具有较好的相关系数，说明该模型可运用于固定床中表面活性剂的吸附。

参考文献：

[1] STEGMANN R， BRUNNER G， CALMANO W， et al. Treatment of contaminated soil： fundamentals， analysis， applications[M]. Berlin： Springer， 2001.

[2] MANN M J， ANDERSON W C， PETERSON G， et al. Innovative site remediation technology： soil washing - soil flushing[M]. American Academy of Environmental Engineers， 1993.

[3] DESHPANDE S， SHIAU B J， WADE D， et al. Surfactant selection for enhancing ex situ soil washing[J]. Water Research， 1999， 33（2）： 351-360.

[4] LAHA S， TANSEL B， USSAWARUJIKULCHAI A. Surfactant–soil interactions during surfactant-amended remediation of contaminated soils by hydrophobic organic compounds： A review[J]. Journal of Environmental Management， 2009， 90（1）： 95-100.

[5] AHN C K， KIM Y M， WOO S H， et al. Soil washing using various nonionic surfactants and their recovery by selective adsorption with activated carbon[J]. Journal of Hazardous Materials， 2008， 154（1-3）： 153-160.

[6] MULLIGAN C N， YONG R N， GIBBS B F. Surfactant-enhanced remediation of contaminated soil： a review[J]. Engineering Geology， 2001， 60（1-4）： 371-380.

[7] LANGMUIR I. The constitution and fundamental properties of solids and liquids Part I Solids[J]. Journal of the American Chemical Society， 1916， 38（38）： 2221-2295.

[8] FREUNDLICH H. Ueber die Adsorption in Loesungen[J]. Physchem， 1996（57）： 385-470.

[9] CESTARI A R， VIEIRA E， VIEIRA G S， et al. Aggregation and adsorption of reactive dyes in the presence of an anionic surfactant on mesoporous aminopropyl silica[J]. Journal of Colloid and Interface Science， 2007， 309（2）： 402-411.

[10] ERDINC N， GOKTURK S， TUNCAY M. A study on the adsorption characteristics of an amphiphilic phenothiazine drug on activated charcoal in the presence of surfactants[J]. Colloids and Surfaces B-Biointerfaces， 2010， 75（1）： 194-203.

[11] ZHU X， ZHAO T. Surface solubilization[J]. J Chem Soc， 1988， 84（11）： 3951-3960.

[12] PUNYAPALAKUL P， TAKIZAWA S. Selective adsorption of nonionic surfactant on hexagonal mesoporous silicates （HMSs） in the presence of ionic dyes[J]. Water Research， 2006， 40（17）： 3177-3184.

[13] LEVITZ P E. Adsorption of non ionic surfactants at the solid/water interface[J]. Colloids and Surfaces A： Physicochemical and Engineering Aspects， 2002， 205（1-2）： 31-38.

[14] GONZALEZ-GARCIA C，GONZALEZ-MARTIN M L，GOMEZ-SERRANO V， et al. Analysis of the adsorption isotherms of a non-ionic surfactant from aqueous solution onto activated carbons[J]. Carbon， 2001， 39（6）： 849-855.

[15] KAYRANLI B. Adsorption of textile dyes onto iron based waterworks sludge from aqueous solution； isotherm， kinetic and thermodynamic study[J]. Chemical Engineering Journal， 2011， 173（3）：782-791.

[16] LIU J， CHEN J， JIANG L， et al. Adsorption of mixed polycyclic aromatic hydrocarbons in surfactant solutions by activated carbon[J]. Journal of Industrial and Engineering Chemistry， 2014， 20（2）： 616-623.

[17] BACCAR R， BLNQUEZ P， BOUZID J， et al. Equilibrium， thermodynamic and kinetic studies on adsorption of commercial dye by activated carbon derived from olive-waste cakes[J]. Chemical Engineering Journal， 2010， 165（2）： 457-464.

[18] KHALED A， NEMR A E， EL-SIKAILY A， et al. Removal of Direct N Blue-106 from artificial textile dye effluent using activated carbon from orange peel： Adsorption isotherm and kinetic studies[J]. Journal of Hazardous Materials， 2009， 165（1-3）： 100-110.

[19] HAN R， WANG Y， ZHAO X， et al. Adsorption of methylene blue by phoenix tree leaf powder in a fixed-bed column： experiments and prediction of breakthrough curves[J]. Desalination， 2009， 245（1-3）： 284-297.

[20] LIU J， YAN Y， ZHANG H. Adsorption dynamics of toluene in composite bed with microfibrous entrapped activated carbon[J]. Chemical Engineering Journal， 2011， 173（2）： 456-462.

[21] CHEN S， YUE Q， GAO B， et al. Adsorption of hexavalent chromium from aqueous solution by modified corn stalk： A fixed-bed column study[J]. Bioresource Technology， 2012， 113（10）： 114-120.