声波与光波(电磁波)传播特性的对比*

冯立峰，王天堃

(哈尔滨师范大学)

1 波动方程

1.1 声波的波动方程

在声场中，应用牛顿定律可得到有关声场中声压p与质点运动速度v的关系方程，即有声波扰动时媒质的运动方程

根据质量守恒定律，媒质在单位时间内由外界流入体积元的质量与从体积元中流出的质量之差等于该体积元质量的增量，可得到关于媒质的质点运动速度v与密度ρ之间的关系，即有声波存在时媒质的连续性方程

对声场中体积元应用热学中的物态方程来描述体积元内的压强、密度、温度之间的变化与联系，并且在低频的情况下，声波的传播过程可近似为绝热过程，经过推导可得到在各处均匀的理想流体媒质中小振幅一维声波的波动方程

将其推广至三维情况可得

1.2 电磁波的波动方程

在均匀绝缘介质中或没有电荷的自由空间(ρ =0，J=0)中，根据麦克斯韦方程组可得到电磁场的运动形式

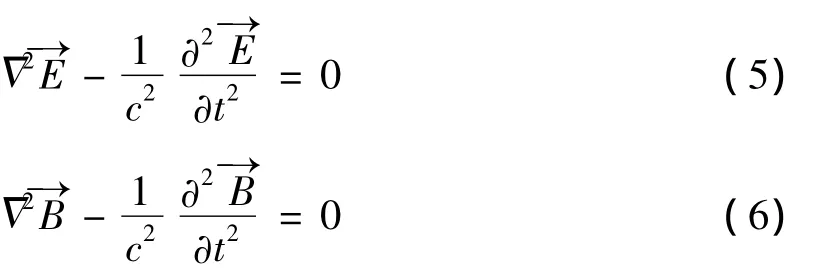
1.3 电磁波与声波波动方程的对比

在形式上，(4)、(5)和(6)式完全一致，并且与简谐振动的形式是一样的，说明他们都是简谐波.(5)式中表示的是真空中电磁波传播的速度，在(4)式中c0也应该是声波在理想气体中的传播速度.进一步对c0研究可知，对于理想气体称之为绝热体积压缩系数，其表征的是由单位压强变化引起的体积的相对变化.可见，在形式上电磁波传播速度的表达式与声波传播速度的表达式一致，且它们的大小都由介质自身的特性决定.

从推导过程来看，声波的波动方程是建立在理想气体之上的，而这种理想气体在现实生活中是不存在的.而电磁波的推导是建立在自由空间或绝缘介质中的，尽管不存在纯粹的自由空间，但是绝缘介质是真实存在的，即声波的波动方程是近似情况下推导出来的，而电磁波则是真实情况下推导出来的.

从实质上看，声波的传播过程本质上是机械振动引起的机械波，是传播介质疏密交替变化的结果.电磁波的传播则是由于空间中的电场和磁场不断变化和互相激发而在空间形成的.声波不是客观存在的物质，它是一种由于媒质的振动而引起的现象，电磁波则不然，它不依靠任何物质而存在，也不是任何其它物质所表现出来的现象，而是客观存在的物质.

从传播条件来看，声波的传播必须有介质的存在，而且介质的压缩性与声波的传播有直接关系，压缩性能越好声波的传播速度越小，压缩性能越差声波的传播速度越快，而电磁波则可以在没有介质的条件下传播.

2 边界条件

2.1 声波边界条件

考虑两种相邻的均匀的理想气体，可推知声波边界条件.两种介质在分界面上声压是连续的.即

此外分界面处质点的切向速度相等，即

2.2 电磁波边界条件

利用麦克斯韦方程组可以得到电磁波的边界条件

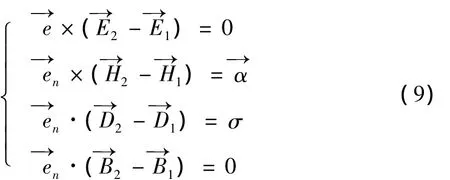
2.3 声波与电磁波边界条件的对比

由(7)和(8)两式可以看出声波边界条件非常简洁，原因是声波的传播是由机械振动引起的，推导过程遵循的是牛顿力学，描述它的物理量都是连续的，不可能发生跃变，而且其本质就是媒质自身振动所产生的现象，不用考虑介质之间的影响.

而电磁波的边界条件在推导过程中考虑了很多因素，因为电磁波的传播不是简单机械振动，而是电场和磁场的相互激发，而且还会受到其他因素的影响，即电磁波作为一种物质，本身具有自己的运动特性，还会受到媒质与它的相互作用.

3 折射与反射

3.1 声波的折射与反射

假设存在一列在xy平面内传播的声波，其传播方向与x轴夹角为θj，反射波的反射方向在xy平面内与x轴成夹角θr，则在介质Ⅰ中，声场是由入射波与反射波共同作用所构成的，同样，在介质Ⅱ中存在透射波，考虑到在分界面处各量之间的关系满足声波边界条件，应该有

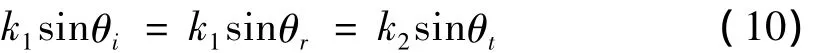
在分界面处反射波声压与入射波声压之比rp和透射波声压与入射波声压之比tp为

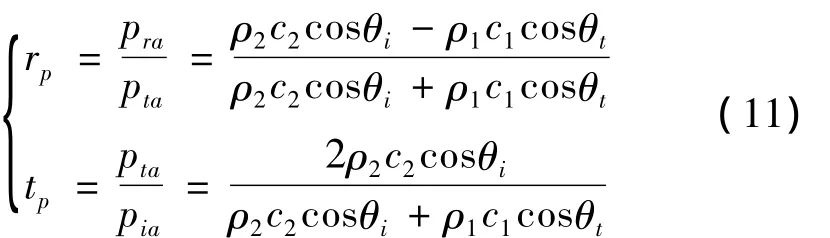
3.2 电磁波的折射与反射

考虑在两接触的介质中传播的电磁波.设入射波、反射波和透射波的传播方向与法线的夹角分别为 θi、θr、θt，根据电磁波的边界条件得到

在分界面处可以得到场强垂直入射面时反射波与入射波之比r和透射波与入射波之比t为

对于场强平行于入射平面时也有类此的振幅比

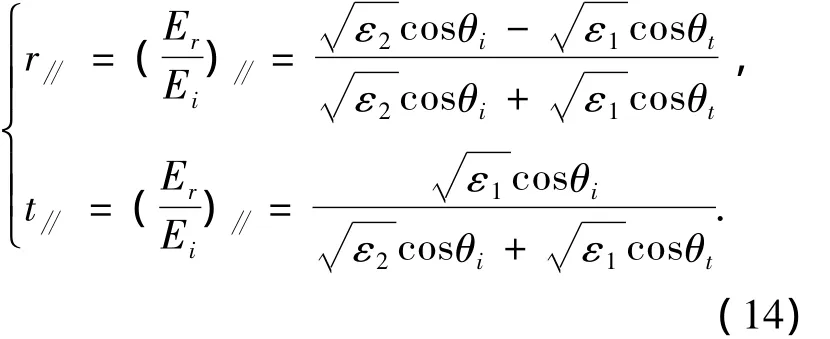
3.3 声波和电磁波折射与反射的对比

通过分析知电磁波在这两种介质中的传播速度的比值可以确定入射角与折射角的大小关系，即入射角与折射角的正弦值的比和两种介质中电磁波的传播速度比相等，也等于其相对折射率.声波在分界面处的入射角与折射角也相等，而入射角与折射角的正弦值等于声波在这两种媒质之中的传播速度比.这与电磁波中的形式完全一样，可以认为不同的介质对于声波有不同的折射率，声波在分界面处正弦值的比值也等于两种介质的相对折射率.当介质Ⅰ的折射率大于介质Ⅱ的折射率时，声波与电磁波都会发生全发射现象.

声波振幅比关系和电磁波振幅比关系有着相似的表达形式，而且其大小都是由两种介质的特性和入射及折射关系决定的，振幅比只与两种介质的特性及入射角有关，而与声波或电磁波本身无关.但是，声波的振幅比只有一个关系式，这是因为描述声波的压强是沿着传播方向传播的，自身没有额外的振动，而描述电磁波的电场及磁场，并不是普通意义上的平面波，它们的传播方向指的是电磁场相互交替激励对方的方向，即它们除了沿着波的传播方向外自身还在做简谐振动，且电场、磁场与传播方向之间满足右手系的关系，所以考虑电磁波在分界面上入射时，要区分电场自身的振动方向.

4 关于多普勒效应的奇妙对比

当有一辆疾驰的赛车从远处向你开来，并且不间断的鸣笛，你会听到汽笛的声音不仅响度越来越大，而且音高也在不断升高，直到经过你面前时，声音的响度和音高达到最大值.当赛车离去时，汽笛的响度和音高降低.这种由于波源或观察者的相对运动而产生的观测频率与波源频率不同的现象就称之为多普勒现象.

在声学中，多普勒效应表述为

其中ν'表示变化后的频率，ν表示波源的频率，ν表示波的传播速度，ν观表示波源与观察者之间的速度.类比到光学中也应有类似的效应，但是由于声波的传播速度在空气中大约为340 m/s，观察者与波源之间的相对速度对于声波的传播来说，是不可以忽略的，所以这种现象在声学中是常见的，而光的传播速度约为3×108m/s，对于宏观世界是不可能有物质的运动速度与其比拟.但是假如有一架以0.6倍光速超高速飞行的红色飞行器飞向我们时，将看到它的颜色将会按照赤橙黄绿青蓝紫的顺序变化，如果可能的话，频率甚至会达到紫外线的范围，即消失在视野中，直到它经过后才会以蓝色出现，远离我们的同时逐渐变为红色，也就是说光波(电磁波)也能产生多普勒效应现象.在光波(电磁波)中，这种现象称之为蓝移或红移.它在天体物理中十分有用，人们可以根据观察到的光或电磁波蓝移或红移的现象来判断一颗星体是接近我们还是远离我们，同样宇宙中出现的红移现象也是说明宇宙膨胀学说的有力证据.

5 结论

通过声波和光波(电磁波)在以上几方面的对比，可以得到以下结论.

5.1 从本质上看

声波是由介质的疏密交替变化而产生的机械波，它是媒质在平衡位置做简谐振动时表现出来的一种现象，只有在有介质的条件下，这种声的传播现象才能产生.而光波(电磁波)自身是一种物质，不依赖于其他物质而产生，所以它的传播不需要介质的存在.

5.2 从均匀介质中的传播规律看

从波动方程中可以得到声波以及光波(电磁波)在均匀介质中的传播规律，但是从表达式中看到，声波的波动方程描述的是介质自身的性质即声压随时间及空间的变化规律，而光波(电磁波)的波动方程表达式描述的是电磁波自身的电场和磁场随时间的变化规律，而描述介质的物理量并没有变化.

5.3 从介质对传播的影响上看

对于声波，它所遵循的是经典力学的物理定律，描述它的物理量是不会产生突变的.在遇到非均匀介质或介质突变的情形下，声波传播特性的改变也是由介质的特性决定的，所以在边界条件中只需考虑描述介质特性的物理量的变化规律.但是对于光波(电磁波)在非均匀介质中或突变介质中的传播规律时，就要考虑它的物质性，不仅由于自身的相互激励不同(一方面是介质的μ及ε的不同导致的，一方面也要考虑电磁波振动方向与入射面的关系)会引起传播规律的变化，还会受介质中的物质的影响产生突变.

5.4 从折返现象来看

从文中看到，声波与光波(电磁波)在介质表面的入射、折射以及透射的规律是相似的，它们之间的角度也满足同样的关系式.声波如同光波(电磁波)一样，也存在全反射现象.在计算振幅比时以及从最后的结果中都可以看出声波与光波(电磁波)在传播特性的相似处，但是也注意到，由于电磁波与声波的本质不同，自身具有振动，所以它的振幅比分两种情况.

5.5 从应用上看

文中提及了一种应用即多普勒效应的应用，无论是声波还是光波(电磁波)都能产生多普勒效应现象，而且多普勒效应都可以应用到测速中，但是应注意到他们彼此存在的条件不同，即声波的传播必须存在介质，而光波则不然，所以在太空中可以利用光波(电磁波)的多普勒效应，又由于水对电磁波的吸收率很大，所以在水中测速时应该利用声波的多普勒效应.

［1］杜功焕.声学基础.南京:南京大学出版社，2012.5.

［2］郭硕鸿.电动力学.北京:高等教育出版社，2008.6.

［3］尹真.电动力学.南京:南京大学出版社，2010.2.

［4］漆安慎.力学.北京:高等教育出版社，2005.6.

［5］赵凯华.光学.北京:高等教育出版社，2004.11.

［6］莫尔斯，英格特，如榆，等.理论声学.北京:科学出版社，1986.

［7］蓝海江.浅谈多普勒效应与多普勒测速［J］.柳州师专学报，1998(3).

［8］田晓培.声波在非均匀介质中的传播.浙江大学，2011.

［9］董秋霞.声场中光波传播特性的研究.空军工程大学学报，2004(4).

［10］徐栓强.漫谈波动.现代物理知识，2002(9).