基于APOS理论的初中生函数概念认知调查
2015-09-06袁柳芳蒋科
袁柳芳++蒋科
1 APOS理论简述
APOS理论是美国的杜宾斯基等人在数学教育研究实践中发展的一种理论,是针对于数学概念学习过程研究的一种建构主义的学习理论,[1]杜宾斯基认为,学生学习数学概念要进行心理建构,这一建构要经历4个阶段:操作阶段(Action)、过程阶段(Process)、对象阶段(Object)和图式阶段(Scheme),取这四个阶段英文单词的首字母,定名为APOS理论[2].这种理论不仅指出学生的学习过程是建构,而且表明了建构的层次.
操作阶段(Action)是学生理解概念的一个必要条件,通过操作让学生亲自体验,感受直观背景和概念间的联系.例如,在有现实背景的问题中建立函数关系:y=x2,需要用具体的数字构造对应:2→4;3→9;4→16;5→25;……通过操作,理解函数的意义.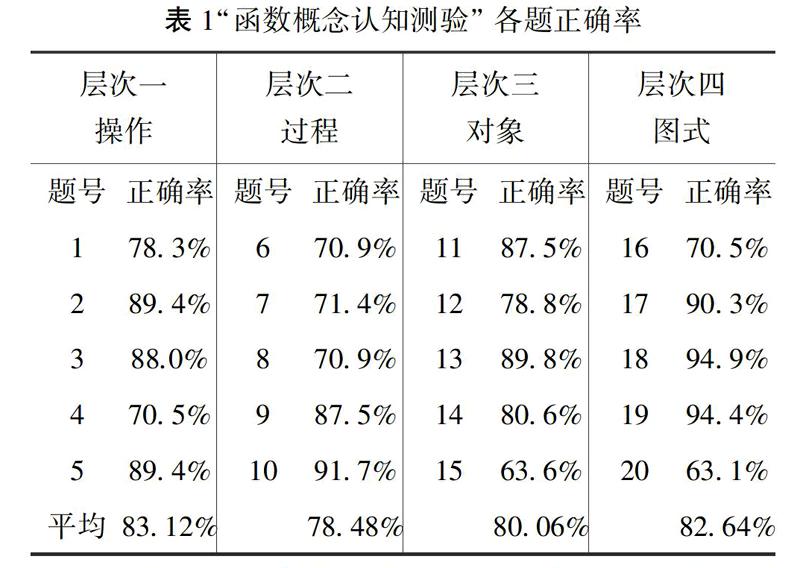
过程阶段(Process)是学生对操作进行思考,经历思维的内化,概括过程,学生在头脑中对活动进行操作和反思,抽象出概念所特有的性质.一般地,有x→x2;其它各种函数也可以概括为一般的对应过程:x→f(x).
对象阶段(Object)是通过前面的抽象认识到了概念的本质,对其进行压缩并赋予形式化的定义及符号,使其达到精致化,成为一个思维中具体的对象,在以后的学习中以此为对象去进行新的活动.比如函数的加减乘除、复合运算等,在表示式f(x)±g(x)中,函数f(x)和g(x)均作为整体对象出现.
图式阶段(Scheme)的形成是要经过长期的学习活动进一步完善,起初的图式包含反映概念的特例、抽象过程、定义及符号,经过学习,建立起与其他概念、规则、图形等的联系,在头脑中形成综合的心理图式[3].
APOS理论提出的数学概念学习的四个阶段,从思维层次上反映出数学概念从具体操作行为到抽象的心理结构的过程性,是概念在头脑中建构的一个连贯顺序,是循序渐进螺旋上升的.
2 研究的设计
2.1 研究工具
本测验工具依据APOS理论各层次的具体建构目标,配合我国现行全日制义务教育数学课程标准的要求,同时参考初中数学教科书,以及函数概念相关研究等文献编制而成,编制试题期间多次修正后,进行预试,根据预试的结果再进行修正,成为正式施测题目.正式测试题“函数概念认知测验”包括20道选择题和2道解答题,选择题分属五个函数概念认知层次,每个层次有五题,另外2道解答题则为研究学生函数概念认知提供参考.利用SPSS 12.0 for windows的分析结果,得到总测验的alpha值为.801,显示此份工具的信度相当高.
2.2 研究对象
为使调查结果具有一定的说服力和推广性,在选择研究样本时考虑所选样本必须具有一定的代表性,且从不同学校选取同一层次上的班级,便于对结果进行比较分析.本研究选取具有代表性的2所初中共490名学生作为样本进行调研.
2.3.1 APOS理论各层次表现 根据表1的数据可以发现初三学生函数概念认知各层次掌握较好,其中对象层次的第15题和图式层次的第20题正确率较低,这两题考察的分别是函数图象上的动点问题和图形运动中的函数关系问题,这类图形运动的问题综合性较强,怎样把动态问题变为静态问题来解是许多学生难以跨越的障碍.
本研究以某一层次正确率达到60%作为通过该层次的标准,例如某个学生在操作层次上的5道题中答对其中任意3道即代表该生通过该层次.由此统计所有样本在各层次上学生通过人数及通过比例.
从各层次的平均正确率和通过比例来看,总体上掌握较好,但是过程阶段正确率和通过率都相对较低,说明在教学中应特别重视学生函数概念抽象的过程,怎样让学生经历思维的内化,概括过程,抽象出概念所特有的性质,是教学的一个难点.这也是高中学生函数学习同样面临的问题.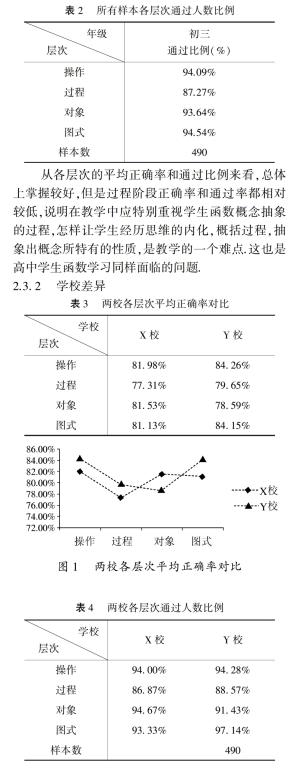
2.3.2 学校差异
图2 两校各层次通过人数比例对比 将两校初三年级学生函数概念认知各层次正确率和通过率进行对比,发现两校学生表现差异不大,总体上Y校比X校表现略好,通过独立样本t检验,表明两校在函数概念认知上没有显著性差异,这也很好的体现了义务教育阶段教育资源均衡化的要求.
2.3.3 性别差异
以性别来看,在各层次上男生表现优于女生.进一步对测试结果进行学校、性别二因子变异数分析,可以发现学校与性别之间无交互作用.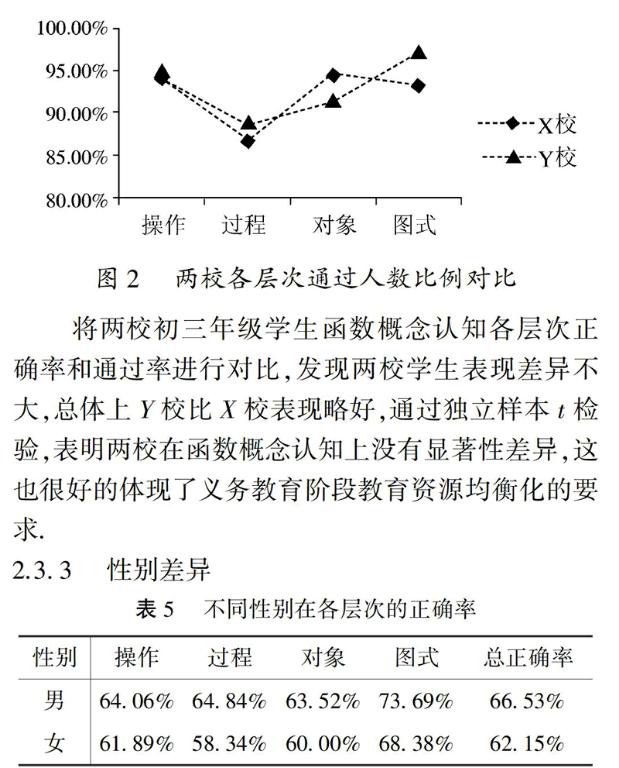
3 结论
(1)初三学生函数概念认知在APOS理论各阶段上掌握较好,但是函数图象上的动点问题和图形运动中的函数关系问题正确率较低,亟待加强.
(2)从各层次的平均正确率和通过比例来看,过程阶段正确率和通过率都相对较低,在教学中应特别重视学生函数概念抽象的过程.
(3)学校之间在函数概念认知上没有显著性差异,这也很好的体现了义务教育阶段教育资源均衡化的要求.
(4)在各层次上男生表现优于女生,且学校与性别之间无交互作用.
4 函数概念认知影响因素分析
学生函数概念认知水平受多种因素的影响,包括教师的教学方式、学生的学习方法、中学数学函数课程的设置等因素.
我国中学数学学习向来重视考试,通过大量的习题训练,获得优异的数学成绩,但缺少对数学概念、方法和思想深刻地理解.正如张奠宙先生撰文指出的,东西方数学教育区别之一是:西方人主张“理解、理解、理解”,而华人则多半主张“练习、练习、练习”[4].
李士锜先生在“熟能生巧吗”一文中指出:“一方面,许多优等生勤奋努力的经验,以及我国、日本等东亚地区在多次国际性评估中成绩名列前茅的事实可以从正面肯定我们的传统做法:大量数学习题训练和经常性测验考试是提高学生成绩的有效途径;另一方面,大运动量训练的‘题海战术使学生和教师的负担不堪忍受,表现出效率低下,抑制学生的创造性和积极性的弊端.”
另外,分析中美两国中学数学课程标准关于函数概念的要求也有所区别.美国的课程标准强调从学前教育到高中的过程中,应帮助学生学习各种函数,特别强调运用函数的多种表征方式,加深学生对函数概念的理解,[5]在不同学段,对函数有不同内容、不同程度、不同范围的要求.学生对函数的认识是循序渐进、逐步提高的.我国数学课程标准中只在初中、高中阶段有函数内容和要求,小学阶段没有[6].
参考文献
[1] 曾国光.中学生函数概念认知发展研究[J].数学教育学报,2002(2):99-102.
[2] 徐立英,张丽娜.APOS理论对函数概念教学的启示和应用[J].高等教育研究,2007(3):73,74.
[3] 濮安山,史宁中.从APOS理论看高中生对函数概念的理解[J].数学教育学报,2007(2):48-50.
[4] 史宁中.中学数学课程与教学中的函数及其思想——数学教育热点问题系列访谈录之三[J].课程·教材·教法,2007(4):36-40.
[5] HamideDogan-Dunlap.reasoning with metaphors and constructing an understanding of the mathematical function concept. In Woo, J. H., Lew, H. C., Park, K. S. &Seo, D. Y. (Eds.). Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education. Seoul: PME. Vol. 2∶209-216.2007.
[6] 全美数学理事会,蔡金法等译.美国学校数学教育的原则和标准[M].北京:人民教育出版社,2004:21-22,36-37,84-86,142-144,204-206,268-277.
