“涉高题”的解法要避免涉高
2015-09-06金绍鑫
金绍鑫



近年来,中考试卷中涉及高中知识的题(简称涉高题)屡见不鲜,大有愈演愈烈之势.对此有人叫好,有人不以为然.更多的是,老师们对涉高题的解题教学困惑,讲又不好讲,不讲又说不过去,真有点左右为难.本文以近年较典型的中考涉高题为例,谈谈解题教学中的难点处置和对题目的看法.
1 “认识图像”涉高题
“认识图像”是初中数学教学的重要内容,也是中考数学试卷中的常客.某次听初三“认识图像”的复习课,遇到这样一个题:
图1如图1,AB是半圆O的直径,点P从点A出发,沿半圆弧AB顺时针方向匀速移动至点B,运动时间为t,△ABP的面积为S,则下列图象能大致刻画S与t之间的关系的是( ).(2014年黄石)
老师让学生讨论此题.
学生1:设AB边上的高为h,则S=12·AB·h=12·2r·h=rh,这是正比例函数,所以选A.
学生2:错了.因为三角形面积由小到大,再由大到小,所以应该选B.
学生2的解答得到了部分同学的认可.
……
学生3:不对.题目问的是S与t之间的关系,而S=rh表示的是S与h之间的关系,应该设法将h换成t,但我不知道怎样换,也不知换出来是什么函数,我猜应该选C.
老师肯定了学生3“将h换成t”和选C的想法,然后讲到:
“点P在弧AB上运动时,随着时间t的增大,点P到AB的距离先变大,当到达弧AB的中点时,最大,然后逐渐变小,直至到达点B时为0.但是,点P到AB的距离的变化不是直线变化.纵观各选项,只有C选项图象符合.故选C.”
学生3的解答很不错,老师的补充讲解反而显得苍白.要想正面回答为什么“点P到AB的距离的变化不是直线变化”就该选C,本身很不容易,涉及高中知识,老师应当从选择题的特殊解法角度去讲,突出“排除法”才是正道理.至于选项C的图像是什么,是不是半圆,是不是抛物线的一部分,在此都不重要.因此,我们可以认为,这个涉高题用于中考没有什么意义,它的意图很明显,就是考排除法,不“涉高”照样可以考排除法.高中生来做这个题也会用排除法,因为写出S与t之间的关系式不容易,即便写出来了也未必知道是什么函数,不便和其对应的图像联系起来,所以此题按惯性思维用推理计算法写出S与t之间的关系式来解走不通.
再看一例.
图2如图2,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( ).(2013年莱芜)
和上题不同的是,此题比较容易写出函数解析式,既可以用高中知识写,也可以用初中知识写:
解法1:计算推理法.
图3如图3,M在AB段时,利用勾股定理和30°角对的直角边是斜边的一半(或者用余弦定理,涉高.)立得NM2=y=x2-x+1,(0≤x≤3)
M在BC段时,作ND⊥BC于D,NM2=y=(5-x)2+3=(x-5)2+3,(3 解法2:排除法. 因为等边三角形ABC的边长为3,N为AC的三等分点,所以AN=1.所以当点M位于点A处时,x=0,y=1. ①当动点M从A点出发到AM=1的过程中,y随x的增大而减小,故排除D; ②当动点M到达C点时,x=6,y=3-1=2,即此时y的值与点M在点A处时的值不相等.故排除A、C.故选B. 这个题的设计就比较好,它沟通了初、高中数学知识的联系,入口宽,方法多样.这样的涉高题就值得推崇.教学时可视班情决定这两种方法的取舍,或用其中一种或两种都用. 2 “阅读理解”涉高题 “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m A.m C.a 按命题者意图解答如下: 图4方程1-(x-a)(x-b)=0转化为(x-a)(x-b)=1,设函数y1=(x-a)(x-b),y2=1,画出两函数的图象,如图4所示.函数y1=(x-a)(x-b)图象为抛物线,开口向上,与x轴两个交点的横坐标分别为a,b(a 由m 综上所述,可知m 本题给出一个知识点,要求学生用此知识点解题(涉高),看似为学生指明了解题方向,实际上限制了学生的思维,学生误以为只能用此方法,可是,用此方法涉及到知识、能力的迁移,难度很大,学生真正能想到上述方法的不多,除非平时老师讲过,学生练过.要是拿给高中生做,只要他学过坐标平移,瞬间就能得出答案. 命题者为了考察学生阅读理解能力,追求创新题,无可厚非,但此题的教学导向可能遭到质疑,因为这样的题目一多,容易诱导教师打着“拓宽”的幌子,补充高中的坐标平移知识. 有人认为,本题考查了二次函数与一元二次方程的关系,考查了数形结合的数学思想.解题时,画出函数草图,由函数图象直观形象地得出结论,避免了繁琐复杂的计算.这种观点是站在命题者的角度看问题,而不是站在初中学生的角度看问题,把一个需要很强迁移能力的解法说成“避免了繁琐复杂的计算”,认为按命题者方法求解很容易,这种说法有失偏颇.
事实上,此题计算并不繁琐复杂.不用题目指引的方法也很容易得出正确选项.利用方程根的意义,得到(x-m)(x-n)=(x-a)(x-b)-1=0,展开后有m+n=a+b,mn=ab-1(用韦达定理也行,课标2011版增加了韦达定理内容),再取满足题意的特殊值作比较即可.取m=0,则a、b互为倒数,设a=12,b=2,则n=2.5;也可取m=1,n=3.5,a=1,5,b=3.所以选A.有的考生不按“规则”出牌,靠上述取特殊值的方法巧妙地得出了答案.
这两种方法,孰难孰易,一目了然,按照题目指引的方法,学生难以做出结果,极有可能诱导老师补充高中知识.对于选择题,人家是怎样解的,你无从知道,也无法左右.因此,本题一相情愿的命题意图很难实现.我们在欢呼某些涉高题如何好的时候,还要看到它自身存在的许多不足.老师们进行题目教学的时候不能完全受制于题目,不能仅仅局限于“形”,还应当从“数”方面考虑,把数形结合思想发挥得淋漓尽致.再看下面一道题.
这也是很典型的涉高题,根据2012年兰州市中考题改编而成:
二次函数y=ax2+bx+c(a≠0)的图象如图5所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( ).
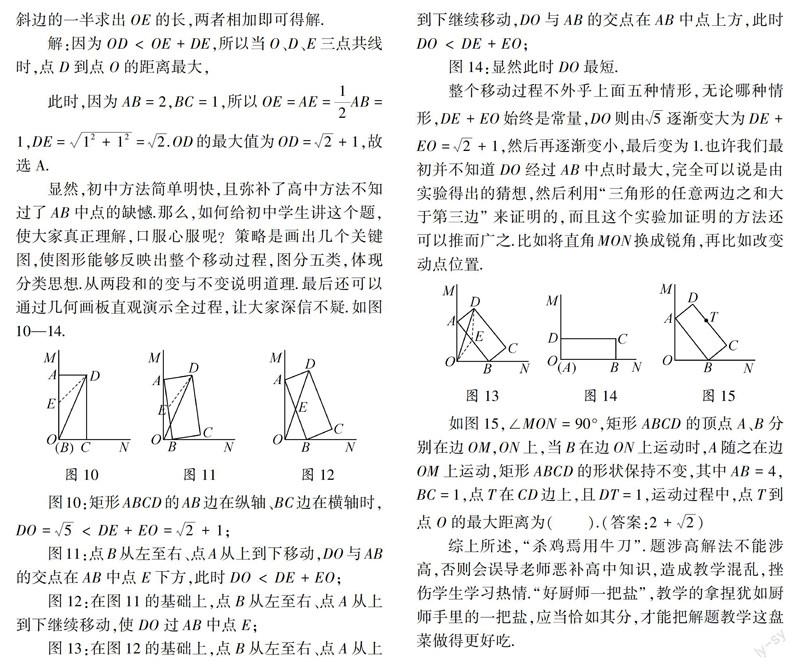
A.0 C.k>2 D.k>3 教学中,老师们普遍采用直观的翻折法(涉高)进行讲解. 图5 图6根据题意得:y=|ax2+bx+c|的图象如图6,因为|ax2+bx+c|=k(k≠0)有两个不相等的实数根,所以k>3.故选D. 这个方法是怎么想到的,却很少有人分析清楚,学生懵里懵懂,没有真正理解.华罗庚先生指出:“数缺形时少直观,形少数时难入微.”这里单纯用翻折法很难“入微”.没有高中解析几何的系统训练,暮然使用翻折法,初中学生既不容易想到,又难于真正搞懂.所以我们应当从学生理解题意做起,从学生最近发展区设计解题教学. (1)设置系列问题引导学生读懂题意 有两个实数根的方程是什么方程?根据绝对值的意义,方程|ax2+bx+c|=k(k≠0)去掉绝对值符号后得到两个什么方程?这两个方程都有根的话,说明原方程|ax2+bx+c|=k(k≠0)有几个根?那么|ax2+bx+c|=k(k≠0)有两个不相等的实数根,必须ax2+bx+c+k=0, 或ax2+bx+c-k=0中的一个方程满足什么条件?从题中图像上看,对于二次函数y=ax2+bx+c(a≠0),当y=-3时,一元二次方程ax2+bx+c=-3有怎样的实根?当y>-3时,关于x的一元二次方程ax2+bx+c=y有怎样的实根?当y<-3时,关于x的一元二次方程ax2+bx+c=y有怎样的实根? (2)读懂题意后引导学生寻求多种解法 对此题而言,学生的最近发展区是什么?是一元二次方程与二次函数的关系.所以,我们应当先从这个关系出发,从数的角度得出下列解法1、解法2. 解法1(构造法):根据图像构造二次函数y=(x-m)2-3,m为任意实数.显然,当y=±k,且0 解法2(判别式法):①ax2+bx+c+k=0,Δ=b2-4ac-4ak≥0,k≤-4ac-b24a=3,即当0 解法1、2让学生先“入微”,然后再让学生从形的方面加强认识.数形结合,相得益彰,既使学生深入理解了本题的解法,又让他们融会贯通了学过的知识. 3 “求最值”涉高题 如图7,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( ).(2012年济南) A.2+1 B.5 C.1455 D.52 这是一个被炒得很热,产生过若干变式的题目.可以用高中的三角法、一元二次不等式等多种方法直接求解(涉高),也可以用初中几何法求解.用几何法求解时,初中学生甚至老师都有疑问:为什么过AB中点的线段DO就是点D到点O的最大距离?怎么想到的?能严格推理证明吗?我们不妨先用一种高中方法求出最大值,消除老师心中的疑虑. 图7 图8如图8,设OA=b,OB=a,则a2+b2=4. 因为△CGA∽△AOB,所以CGAO=GAOB=12,所以CG=12AO,GA=12BO. 则OC2=CG2+GO2=(12AO)2+(GA+AO)2=(12b)2+(12a+b)2=b2+ab+1. 设a=kb,代入a2+b2=4,得b2=4k2+1, 所以OC2=b2+ab+1=4k2+1+k·4k2+1+1,所以OC2(k2+1)=4+4k+k2+1. 整理成关于k的一元二次方程(OC2-1)k2-4k+OC2-5=0, Δ=16-4(OC2-1)·(OC2-5)≥0,化简得OC4-6·OC2+1≥0, 解得OC2≤3+22,OC≤3+22=2+1,所以OC的最大值是2+1. 高中方法运算量大,技巧性强,且并不容易知道DO过了AB中点,这是很遗憾的. 我们再来看看初中解法. 图9分析:如图9,取AB的中点E,连接OE、DE、OD,根据三角形的任意两边之和大于第三边可知当O、D、E三点共线时,点D到点O的距离最大,再根据勾股定理列式求出DE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.
解:因为OD 此时,因为AB=2,BC=1,所以OE=AE=12AB=1,DE=12+12=2.OD的最大值为OD=2+1,故选A. 显然,初中方法简单明快,且弥补了高中方法不知过了AB中点的缺憾.那么,如何给初中学生讲这个题,使大家真正理解,口服心服呢?策略是画出几个关键图,使图形能够反映出整个移动过程,图分五类,体现分类思想.从两段和的变与不变说明道理.最后还可以通过几何画板直观演示全过程,让大家深信不疑.如图10—14. 图10:矩形ABCD的AB边在纵轴、BC边在横轴时,DO=5 图11:点B从左至右、点A从上到下移动,DO与AB的交点在AB中点E下方,此时DO 图12:在图11的基础上,点B从左至右、点A从上到下继续移动,使DO过AB中点E; 图13:在图12的基础上,点B从左至右、点A从上到下继续移动,DO与AB的交点在AB中点上方,此时DO 图14:显然此时DO最短. 整个移动过程不外乎上面五种情形,无论哪种情形,DE+EO始终是常量,DO则由5逐渐变大为DE+EO=2+1,然后再逐渐变小,最后变为1.也许我们最初并不知道DO经过AB中点时最大,完全可以说是由实验得出的猜想,然后利用“三角形的任意两边之和大于第三边”来证明的,而且这个实验加证明的方法还可以推而广之.比如将直角MON换成锐角,再比如改变动点位置. 如图15,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=1,点T在CD边上,且DT=1,运动过程中,点T到点O的最大距离为( ).(答案:2+2) 综上所述,“杀鸡焉用牛刀”.题涉高解法不能涉高,否则会误导老师恶补高中知识,造成教学混乱,挫伤学生学习热情.“好厨师一把盐”,教学的拿捏犹如厨师手里的一把盐,应当恰如其分,才能把解题教学这盘菜做得更好吃.