激光主动探测成像中全景拼接的算法研究

马雪松，张海洋，韩 磊，赵长明，杨苏辉

（北京理工大学光电学院，北京100081）

·图像与信号处理·

激光主动探测成像中全景拼接的算法研究

马雪松，张海洋，韩 磊，赵长明，杨苏辉

（北京理工大学光电学院，北京100081）

激光主动探测成像是将激光技术、距离选通技术、微弱目标的成像处理等技术结合应用的一项新技术。因其分辨率高、抗干扰能力强、能够生成三维像的优点，广泛应用于各种探测领域。但这种方式获取的图像一般视场角偏小，不利于全局的观察和分析。本文描述了一种通过改进的并行SURF算法检测场景角点特征，能够高速实时地将相邻场景焦点特征相匹配的全景拼接方法。测试了这种方法的运行效率和拼接效果。利用改进后的SURF算法将小视角的图像拼接起来，增大了可视范围，提高了观察和分析的综合能力。并且将这一方法运用到了3D成像激光雷达距离信息的拼接中，测试了效果，验证了其可行性。本文提出的快速配准拼接算法，为高速实时大视场观察奠定了理论和实验基础。

主动探测；图像处理；特征识别；全景拼接

1 引 言

全景拼接技术是图像处理领域中的重要技术之一，它可以弥补激光探测中，探测视场角过小［1-2］，不利于全局观察的缺陷，因此被广泛应用于虚拟现实、遥感图像处理、视频压缩和传输等领域。目前有很多方法可以进行全景拼接，有Szeliski基于运动的方法［3］，Peleg和Herman的多重投影（Manifold-Projection）拼接法［4］，Kyung Ho的等距匹配法［5］，以上这些都是直接从图像的重叠区域中对应像素灰度值出发去考虑，由于重叠区域有大量像素数需要统计，并且要求图像“亮度恒定”，所以在实际应用上存在一些局限。为了解决以上缺点，出现了由特征匹配出发的拼接算法［6］，典型的有基于相位一致性和Hough变换的图像配准方法［7］，Harris和Stephens的Harris角检测算子［8］，尺度不变特征变换匹配（SIFT）算法［9-10］，和近年出现的加速鲁棒特征（SURF）算法，这几种算法都是将两幅图像的角点特征进行匹配，从而完成图像拼接。

本文提出了一种改进的并行SURF算法，通过并行运算和重写部分代码达到了提高算法运行效率的作用。这一改进加快了SURF算法的速度，达到了高速实时处理的要求。并且本文将SURF算法运用于3D成像激光雷达的应用，验证了其可行性。

2 SURF算法原理

SURF算法的第一步，也是其核心的是构建Hessian矩阵，给定一个图像I上的点X=（x，y），则点X在尺度σ上Hessian矩阵为［11］：

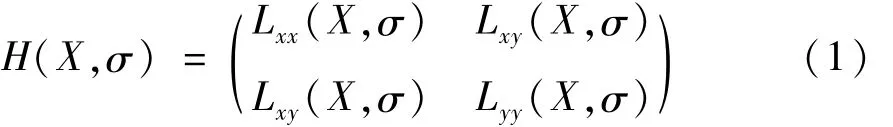
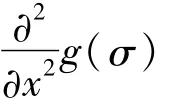
SURF算法巧妙之处在于将图像处理成积分图像，这样要计算Hessian响应时，只需要计算三次加减法即可。由于采用了积分图像和盒子滤波器，所以在建立尺度空间时，可以采用不同的图像金字塔构建方法，图像大小不变而改变了Gaussian盒子滤波器的大小。

尺度空间由不同的组构成，第一组的最小尺度是9，那么经过差值之后，下一组的最小高斯函数的尺度就是σ=1.6=1.2，盒子滤波器的最小尺寸为12×12，最大的高斯函数尺度为σ=3.2= 1.2，盒子滤波器的最小尺寸为24×24［12］。尺度空间各组和组内每层的分布如图1所示。

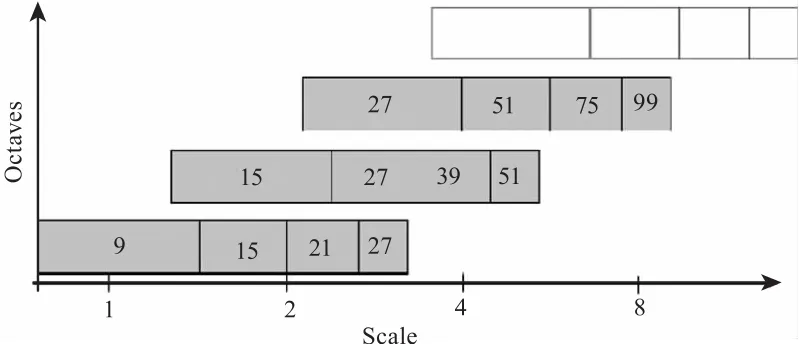
图1 三个不同组的盒子滤波器尺寸示意图Fig.1 Graphicalrepresentationofthefilter sidelengthsforthreedifferentoctaves

通过以上步骤得到多层尺度空间数据后利用三维空间上｛x，y，σ｝的非最大值抑制来寻找极值点，x，y表示横纵坐标，s代表尺度。在得到极值点后，需要用插值迭代的方法获得更高尺度精度，需要用到Brown提出的方法［13］，为此需要将检测点处的Hessian函数的特征值H（x，y，σ）进行泰勒展开，结果为：

当极值点的值为0时得到插值位置^x=（x，y，σ），代入式（2），该微分是对邻近像素的有限差分逼近，当^x大于0.5时根据结果调整位置再一次进行以上的差值运算，直到^x的值小于0.5或者差值次数超过阈值次数为止。

在兴趣点处用Haar小波计算其一定大小邻域处的Haar小波响应的统计，从而计算出兴趣点的主方向和特征描述向量［14］。最后只需比较两幅图像间兴趣点描述子向量的距离，就可以完成两幅图像间特征点的匹配。

3 SURF算法的改进

尽管SURF算法在特征匹配算法中具有相对不错的效率，也因为使用了boxfilter和积分图像提高了效率，但是如果要用在实时处理上，其效率还是远远不够的。现在主要运用的OpenSURF其匹配两幅图像所需要的时间往往需要在800ms以上，对于现在很多实时系统来说这种效率是无法容忍的。所以需要改进SURF算法，在保留其精准度的同时提高它的效率。

首先如上一章所述，SURF算法流程如图2所示。

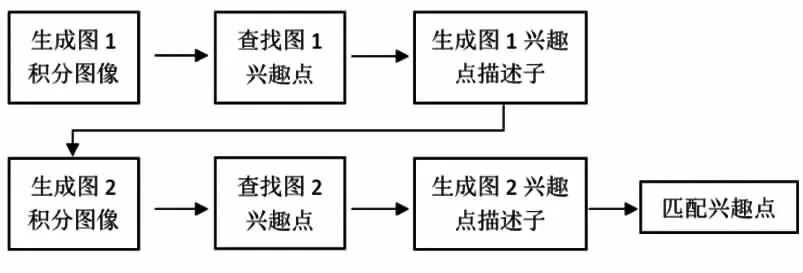
图2 传统的SURF拼接算法流程图Fig.2 TheflowchartoftraditionalSURFalgorithminstitching

如图2所示的是传统的SURF算法的流程图，可以看到这一流程完全是串行化的，实际上从图中可以看出输入的图像一和图像二做的完全是同样的操作，所以完全可以把这个两个流程做并行化处理，理论上可以提升一倍的效率。并行化后的流程图如图3所示。

图3 并行的SURF拼接算法流程图Fig.3 The flowchart of parallel SURF algorithm in stitching

其次，SURF算法在生成积分图时是从BITMAP类上提取像素值，这样每处理一个像素点就要做一次提取，这样是相当耗时的，所以，在运行SURF算法之前，将两幅图像预处理为一组RGB矩阵，再改写SURF算法直接从矩阵中读取数据，这样使得数据的读取操作变得更加容易，可以很大程度上加快SURF算法的处理效率。至此，将输入数据类型和程序流程改写完成。可以对代码具体的SURF算法进行改写，这里主要是对算法中的循环进行Parallel并行化改写。

用不同大小尺度的Gaussian二阶偏导数对改进前的代码进行多次测试得到平均数据，得到了如表1所示的未经过优化代码的数据。

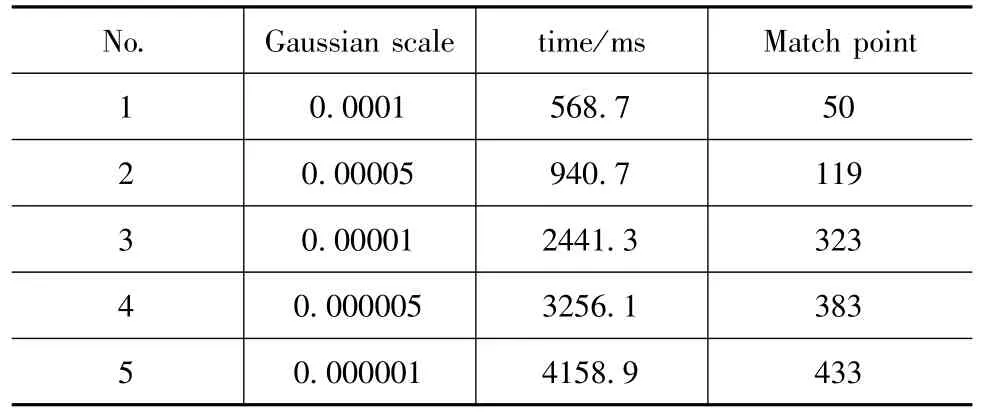
表1 未经过优化代码运行数据Tab.1 The data of SURF before optimising

从表1中可以看出，随着Gaussian scale的减小，图片处理的越细密，匹配点数越多，若要使得匹配点达到50个，则代码的执行时间平均为568.7 ms，这样的匹配点数是SURF拼接的基本条件。这也就意味着，在不对代码进行优化的情况下，若要保证两幅图像成功拼接，需要560.7 ms以上的时间来运行算法，这样的表现达不到实时系统的要求。

经过上文所述的并行优化、输入优化和数据结构的优化后再次在同样的硬件条件下处理相同的两幅图像多次，记录多组数据取得平均值，得到了优化后的算法运行数据，如表2所示。

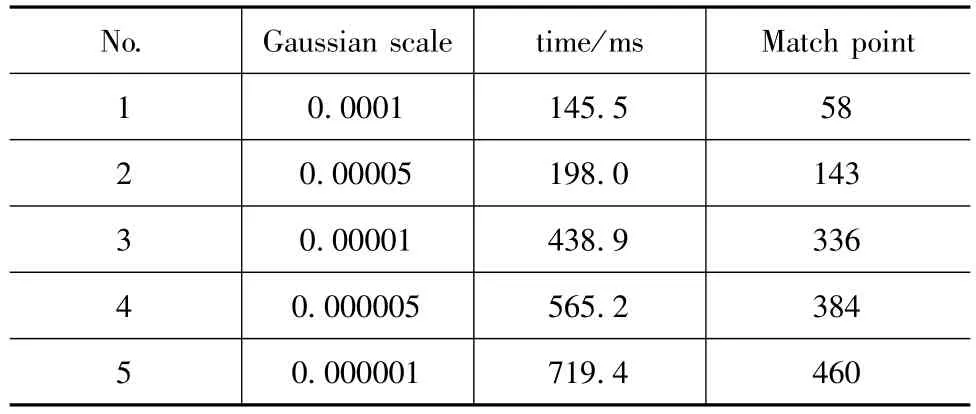
表2 经过优化代码运行数据Tab.2 The Data of SURF after Optimising

表2显而易见的表明了算法的性能改善，在Gaussian scale为0.001时，不仅算法效率有了极其显著的提升，而且在特征点数量上也有了一定的改善，这说明本文所述的算法优化是相当有效的。

图4显著地表现了算法优化的效果，在代码优化前点数时间比最大可达到0.13，但是经过优化后这一比例最大达到0.76，最小时也有0.4，最小值是优化前最大值的近四倍。图中的折线代表优化比，代表不同scale下点数时间比的优化倍数，这一倍数最大可达到5.85。在实际应用中当匹配点数足够时，更多的匹配点数并不能带来更好的肉眼可见的拼接效果，在这种情况下，时间方面的优化就显得更为重要。

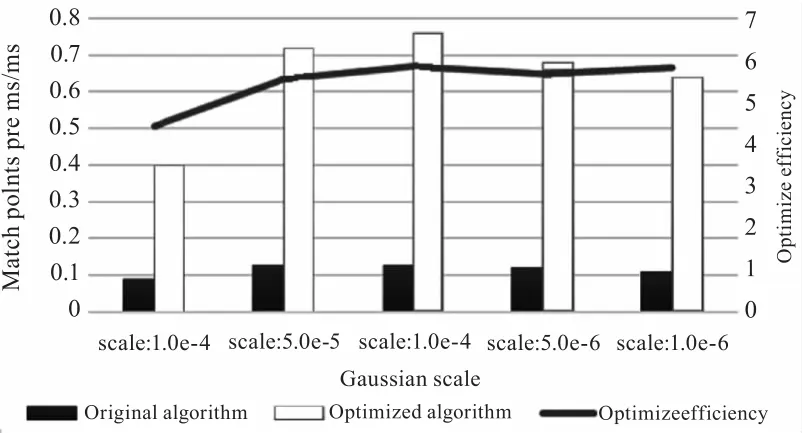
图4 算法效率优化效果示意图Fig.4 The Efficiency Result after Optimizing

在时间上的效果可以从图5中明显地表现出来，对比之下优化后的时间显著减少，并且Gaussian scale越小算法处理图像处理的越细腻，这种优化效果越明显，最后收敛在0.17处，这表明只从时间角度上说，本文所述的优化可使时间效率提高近六倍。

以上证明了优化后的SURF算法在效率上的确得到了显著的提高，下面验证优化后的拼接效果。匹配并拼接两幅640×480的图像在scale为0.000005时经327.6 ms匹配拼接完成，左边图像检测出750个兴趣点，右侧图像检测出803个兴趣点，匹配点数264。优化后的拼接效果如图6所示。

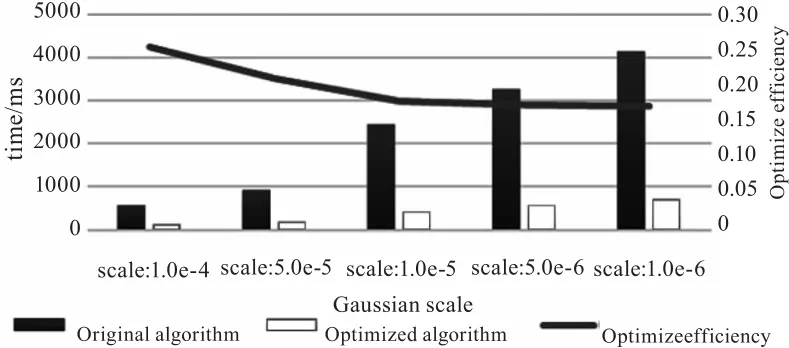
图5 算法时间优化效果图Fig.5 The Time Result after Optimizing

图6 的拼接前后对比图表现出了算法的良好拼接效果，算法成功地对两幅图像进行了拼接。证明了本文所做的优化一方面保证了算法的精确性，提供了良好的拼接效果，另一方面极大地提高了算法的效率。

图6 算法优化后拼接效果图

经过本文优化的SURF算法与其他算法相比，具有非常大的优势。这里将本文的优化算法与一般的Accord.Net库提供的拼接算法做拼接时间上的比较，两种算法处理同样一幅图像，数据如表3所示。

表3 优化的SURF算法与Accord.Net的拼接算法对比Tab.2 The data of SURF after optimising v.s Accord.Net

从表中可以看出，本算法与其他算法相比具有很大的优势。匹配点数量上可以发现，两种算法的相差无几，所以在同一幅图的拼接效果上也是相同的。在时间上本算法只需要Accord.Net的三分之一的时间就可以完成效果相同的拼接效果。所以说，本算法与其他算法相比也具有相当大的优势。

4 SURF算法在3D图像拼接上的应用

如前文所述，在做图像拼接时，优化后的SURF算法在时间和精确性上都具有很好的性能。那么从理论上来说SURF算法同样可以用于3D图像的拼接上，这一方法的实现为3D成像激光雷达的结果显示带来了极大的方便。

为了便于查看拼接效果，将3D成像激光雷达采集到的深度信息转化为灰度图进行显示，拼接效果如图7所示。

图7 3D成像激光雷达深度信息拼接效果图Fig.7 Stitching result of the distance Information of 3D Image Laser Radar

在图7中，（b）是未经处理过的深度信息等效出的灰度图像。将深度信息分割后可以还原出图7（a）中的两个图像，将分割出的两组距离信息输入上文优化后的算法中。经过61.0 ms的处理，可以看出得到了八对匹配度良好的匹配点，算法输出到重新拼接好的矩阵，还原为灰度图如7（c）所示。对比原距离信息还原出的图7（b）和再拼接后得到的距离信息还原出的图7（c），可以看出除了图像的下边缘由于拼接产生的锯齿瑕疵外，剩余区域几乎没有差异。

以上试验可以验证经过本文所述方法优化的SURF算法，完全可以用于3D成像激光雷达深度信息的拼接、还原工作中，这一应用会为3D成像激光雷达带来视角更大、信息更加全面的显示效果。

5 结 论

文中采用了并行化算法和优化算法输入数据类型的方法将SURF算法进行了改进。从得到的数据来看，不论算法的整体效率还是时间效率上都有了很大的提高，而且算法对图像的处理效果并没有因为效率的提高而变差，与预期相符合。这为SURF算法在实时系统上的运用奠定了基础。本文在第三部分进行了将SURF算法运用在拼接3D成像激光雷达所得到的深度数据的试验，从实验结果可以看出，这一方法是完全可行并且有效，这为3D成像激光雷达的数据显示提供了一个新的思路。虽然本次优化已经将SURF算法的效率显著提高，但是通过分析还是有一定优化的余地，例如改变算法细节的数据结构，优化其中对于数据的查找效率，这可以进一步发掘该算法的潜力，为实际运用带来便捷。

［1］WANG Min，SONG Liwei，QIAO Yanfeng，et al.External field stitching technology for high speed targetmeasuring and its implementation［J］.Optics and Precision Engineering，2010，18（9）：2069-2076.（in Chinese）

王旻，宋立维，乔彦峰，等.外视场拼接测量技术及其实现［J］.光学精密工程，2010，18（9）：2069-2076.

［2］YU Xiaobo，SHENG Lei.Image stitching of multi-lens with large visual field in range instrumentation［J］.Optics and Precision Engineering，2008，16（11）：2144-2150.（in Chinese）

于晓波，盛磊.靶场测量中多镜头大视场视频图像的拼接［J］.光学精密工程，2008，16（11）：2144-2150.

［3］SzeliskiR.Image mosaicking for tele-reality applications［C］.IEEE，1994（1）：44-53.

［4］Peleg S，Herman J.Panoramic mosaics by manifold projection［C］.IEEE，1997：338-343.

［5］H JKyung，K JSoon.Constructing cylindrical panoramic image using equidistantmatching［J］.Electronics Letters.1999，35（20）：715-1716.

［6］ZHAO Xiangyang，DU Limin.An automatic and robust imagemosaic algorithm［J］.Journal of Image and Graphics，2004，9（4）：417-422.（in Chinese）

赵向阳，杜利民.一种全自动稳健的图像拼接融合算法［J］.中国图象图形学报，2004，9（4）：417-422.

［7］C Harris，M Stephens.A combined corner and edge detector［C］//Proc of the 4th Alvey Vision Conference，1988，88：147-151.

［8］D G Lowe.Object recognition from local scale-invariant features［C］//Proc of the ICCV，1999：1150-1157.

［9］YUAN Jinsha，ZHAO Zhenbing，GAOQiang，etal.Review and prospecton infrared visible image registration［J］.Laser&Infrared，2001，39（7）：693-699.（in Chinese）

苑津莎，赵振兵，高强，等.红外与可见光图像配准研究现状与展望［J］.激光与红外，2009，39（7）：693-699.

［10］H Bay，A Ess，T Tuytelaars，et al.Speeded-up robust（SURF）［J］.Computer Vision and Image Understanding，2008，110（3）：346-359.

［11］H Bay.From wide-baseline point and line correspondences to 3D［D］.Swiss：Swiss Federal Institute of Technology，2006：19-23.

［12］M Brown，D G Lowe.Invariant features from interest point groups［C］.British Machine vision Conference，2002：656-665.

［13］H Bay，B Fasel，L Van Gool.Interactive museum guide：Fast and robust recognition ofmuseum objects［C］//Proc of the first internationalworkshop onmobile vision，2006.

［14］H Bay，T Tuytelaars，L Van Gool.SURF：Speeded uprobust features［C］//Proc of ECCV，2006，3951：404-417.

Research on panoram ic stitching in laser active imaging

MA Xue-song，ZHANG Hai-yang，HAN Lei，ZHAO Chang-ming，YANG Su-hui
（School of Optoelectronics，Beijing Institute of Technology，Beijing100081，China）

Laser active imaging combines laser technology，range-gated technology，weak target imaging technology and so on.Because of its high resolution，strong anti-interference ability and the ability to generate three-dimensional image，it is widely used in various areas of detection.But in this way，the image's field of view is usually small，which is not conducive to global observation and analysis.A panoramic stitchingmethod based on the improved SURF algorithm is proposed，and it can quicklymatch target features of adjacent scenes.The efficiency of this approach and stitching effect are tested through the experiments.The results show that thismethod can increase the visible range and improve comprehensive ability of observation and analysis，which lays a theoretical and experimental foundation for highspeed real-time large field of view observation.

active detection；image processing；feature recognition；panoramic stitching

TP301

A

10.3969/j.issn.1001-5078.2015.08.021

1001-5078（2015）08-0977-05

马雪松（1989-），男，硕士，从事图像处理算法和探测器性能分析。E-mail：2120120697@bit.edu.cn

张海洋（1981-），男，讲师，主要研究领域为固体激光器及激光探测技术。E-mail：ocean@bit.edu.cn

2014-12-26；

2015-01-13