基于滑模观测器的交流伺服电机无传感器控制*

郭超伟，　高艳霞，　张曲遥，　宋文祥

(上海大学 机电工程与自动化学院，上海　200072)

基于滑模观测器的交流伺服电机无传感器控制*

郭超伟，高艳霞，张曲遥，宋文祥

(上海大学 机电工程与自动化学院，上海200072)

研究了一种基于滑模观测器的永磁同步交流伺服电机无传感器控制方案。通过对静止坐标系中永磁同步电机(PMSM)数学模型的分析，在滑模电流观测器基础上引入扩展反电势(EEMF)估计值，其中包含传统反电势及与电机凸极性相关的电压分量，构造了相应的滑模观测器来估计两相静止坐标系中EEMF分量。通过分析抖振存在的原因，采用Sigmoid函数代替常数切换函数来减小抖振，并利用扩展龙贝格观测器观测出转子的速度和空间位置。仿真结果验证了控制方案的有效性和可行性。

交流伺服电机； 无传感器控制； 滑模观测器； 扩展龙贝格观测器

0　引　言

永磁同步电机(Permanent Magnet Synchronous Motor， PMSM)具有高转矩惯性比、高能量密度、高效率、高可靠性等优点，高性能伺服系统大多采用永磁同步型交流伺服电动机，近年来在机器人、航空航天、电动汽车、工业控制等领域获得了越来越广泛的应用与发展[1]。高性能交流伺服系统需要有精确的转子速度和位置信息，通常通过位置传感器来获得，但位置传感器的使用增加了安装尺寸和系统成本，降低了系统的可靠性和抗干扰性能，限制了系统的使用范围。采用无位置传感器控制技术有利于改善交流伺服系统可靠性，降低系统成本以及对使用环境的要求，具有重要研究意义[2-3]。

无传感器控制的核心是转子位置和转速的估计。系统调速性能的好坏主要取决于状态估计的精度和动态响应速度。目前，按照电机运行的适用范围，无传感器控制主要分两种技术： (1) 利用电动机的空间凸极效应[2，4]。该方法可应用于较宽速度范围，且低速时也可得到较好的估算结果，但具有高频噪声的问题，只适于内嵌式电机。(2) 状态观测器法[5]，直接或间接地从电机反电动势中提取位置信息。这类方法具有良好动态性能，适于表贴式和内嵌式电机，但在低速特别是零速时转子位置估算困难，目前只适合于中高速场合。因此，研究一种适用于两种电机的较宽运行速度范围的无传感器控制算法是关键。

滑模变结构控制是一种解决非线性系统问题的综合方法，对系统数学模型精确度要求不高，对系统参数变化、内部摄动及外界环境扰动具有自适应性，故具有很强的鲁棒性[6]。在基于状态观测器模型的方法中，滑模观测器(Sliding Mode Observer, SMO)的估算方法既适用于表贴式PMSM，也适用于内嵌式PMSM，而且估算转子位置准确、结构简单、容易实现。

本文采用SMO估计反电动势，为了减小抖振，SMO中采用Sigmoid函数代替常数切换的控制函数，采用扩展龙贝格观测器，将转矩指令作为龙贝格观测器的前馈输入，以获得转子位置的零相位滞后估计。最后，通过仿真验证了所设计的SMO的正确性。

1　PMSM无传感器矢量控制系统

PMSM定子上有A、B、C三相对称绕组，转子上装有永久磁钢，定子与转子通过气隙磁场耦合。假设磁路不饱和，在空间磁场呈正弦分布，不计磁滞和涡流损耗影响条件下，得到PMSM在d、q定子旋转坐标系下的数学模型为

(1)

式中：ud、uq、id、iq——旋转坐标系下的电压和电流；

Ld、Lq——电机直轴和交轴电感；

p——微分算子；

Rs——定子相电阻；

ωr——转子电角速度；

ψm——转子磁链。

将式(1)转换到α、β静止坐标系下为

(2)

其中：

(3)

电压方程中电流系数矩阵包含了与转子位置有关的系数Lα、Lβ、Lαβ，即该矩阵是时变而非固定不变的，难以转换为以电流为变量的状态方程。

将式(1)改为

(4)

其中： λm=(Ld-Lq)(id-piq/ωr)+ψm。

式(4)转换到α,β静止坐标系下为

(5)

式(5)为同步电机数学模型的一般形式，若Ld=Lq，就等同于表贴式同步电机(Surface Permant Magnet Synchronous Motor, SPMSM)数学模型；若ψm=0，则成为同步磁阻电机模型。基于该数学模型，可以很方便地将应用于SPMSM的无传感器控制方法应用于IPMSM。

EEMF中包含有iq的微分项，意味着即使转速接近为零，只要iq在变化，EEMF就不会为零。这一特点使得低速甚至零速运行时位置、速度估计成为可能[5]。

转矩方程：

Te=Pn[ψmiq+(Ld-Lq)idiq]

(6)

运动方程：

(7)

式中：Te——电磁转矩；

Pn——电机极对数；

TL——负载转矩；

J——转动惯量；

ω——转子机械角速度。

由式(6)可知，控制d轴电流id=0，则Te=Pnψmiq，所加定子电流全部用于产生电磁转矩。本文采用id=0的矢量控制策略，该策略的优点是相同电磁转矩下电机铜耗小、效率高。永磁电机无传感器控制系统结构框图如图1所示。

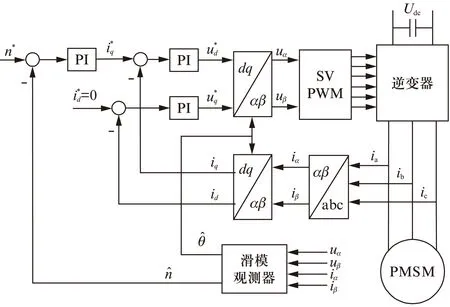
图1　永磁电机无传感器控制系统框图

2　SMO设计

SMO模型可以根据电机在α、β坐标系下的模型来建立。它通过不断获取电流估计值和测量值之间的偏差来修正模型，使两者之间的偏差逐渐消失，以实现对转子转角和速度的估计。

根据滑模变结构理论[6]，构造出SMO：

(8)

式中：x∈Rn;u∈Rm;A,B(x)∈Rn*m。

定义滑模面：

(9)

控制函数为

(10)

为了便于应用SMO观测EEMF，将式(5)的电压方程改写为电流的状态方程形式：

(11)

根据PMSM在α、β静止坐标系下的数学模型，构造传统SMO如下:

(12)

Ksw——滑模系数，此系数的选取必须满足滑模存在性和可达性。

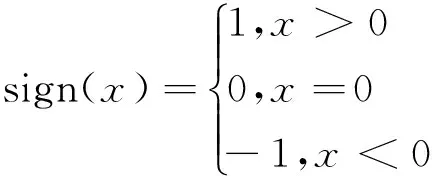
(13)

由于实际系统非理想开关特性(具有时间和空间滞后)，当系统的轨迹到达切换面时，控制作用对状态的准确变化被延迟一定时间，并且在状态空间中存在一个状态量变化的“死区”，所以导致光滑的滑动模态上叠加一个锯齿形的轨迹。

抖振的存在不仅影响控制的精确性，增加能量损耗，而且很容易激发系统中高频未建模动态部分，破坏系统性能，甚至使系统产生振荡或失稳，损坏控制器部件，因此抑制抖振显得极为重要[7]。

图2　Sigmoid函数曲线

采用Sigmoid函数的SMO为

(14)

其中，a为Sigmoid函数的斜率，这里取a=1，由式(11)减去式(14)得

(15)

(16)

式中： eα、eβ——包含有高频分量的反电动势信号。

通过对其进行低通滤波得到连续的反电动势：

(17)

式中： ωc——低通滤波器的截止频率。

由上述分析可得到扩展反电动势SMO的结构如图3所示。

图3　扩展反电动势SMO结构

3　转子速度和位置估计

由传统的滑模电流观测器可获得扩展反电势等效信号，但是还包含高频分量，需要通过低通滤波器进行滤波后得到所需要的连续信号。低通滤波器的使用会带来相位延迟的问题，并且延迟的相位与滤波器截止频率以及输入信号的角频率有关，因此，采用对观测得到的反电动势取反正切函数计算位置信息的方法必须进行角度补偿。

采用带有电磁转矩前馈控制的扩展龙贝格观测器，可以滤除测量干扰信号并实现零相位滞后估计[10]。扩展龙贝格观测器结构如图4所示。

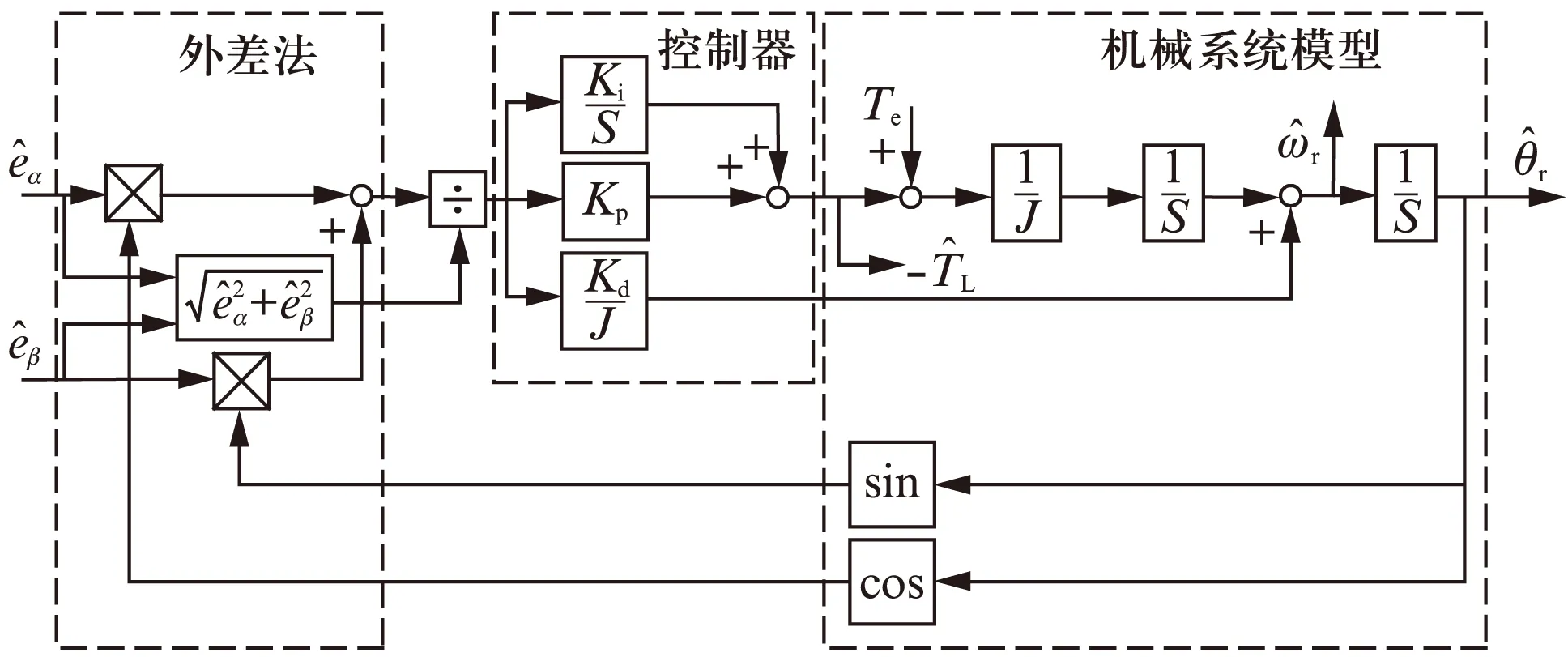
图4　扩展龙贝格观测器

通过外差法和归一化运算得到相位跟踪误差信号，只要调节跟踪误差信号趋近于零，就可以保证估计的转子位置角收敛于实际的转子位置角。

由图4给出的扩展龙贝格观测器结构，可以得到估计转子速度和位置的传递函数：

(18)

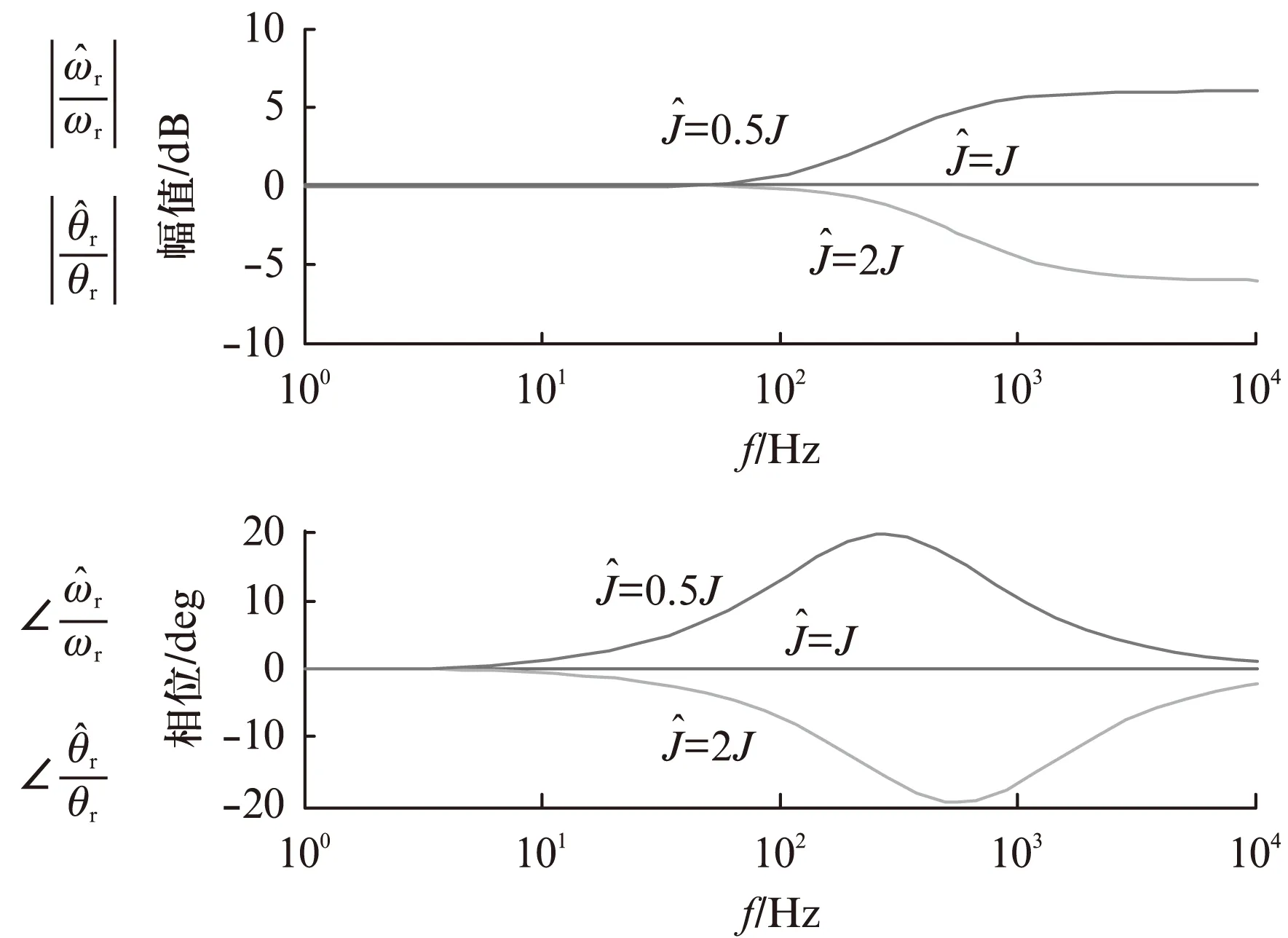
图变化时转子位置观测器估计精度的幅频响应

4　仿真结果

本文采用MATLAB/Simulink建立系统控制模型来验证所提出方案的可行性。电机模型由Simulink内部提供，额定相电压Us=220V，额定转速2000r/min,额定转矩Te=9.55N·m，定子电阻Rs=0.17Ω，绕组直轴和交轴电感分别为Ld=5mH、Lq=8.5mH，转动惯量J=0.0012kg·m2，永磁体磁链ψm=0.175Wb，极对数pn=4。

电机空载条件下，在t=0时刻设定转速450r/min， t=0.5s时刻转速上升为750r/min，设定转速、估计转速与实际转速波形如图6所示。由结果可以看出，估计转速能够很快跟随设定转速，并且收敛于实际转速，系统具有良好的动、静态性能。

图6　转速波形

估计转速与实际转速的偏差如图7所示，可看到电机稳态运行时估计转速与实际转速偏差在5r/min以内，能满足系统的控制需求。

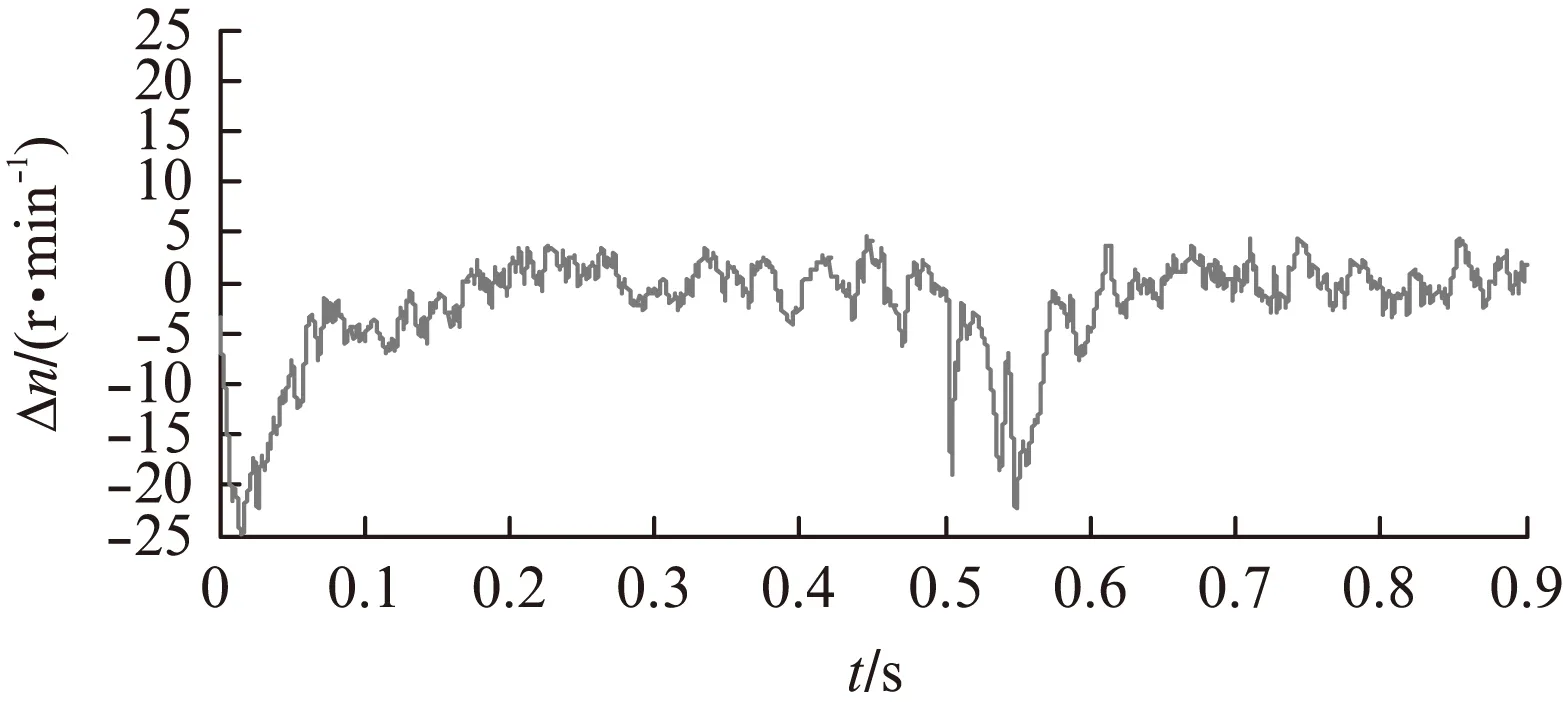
图7　估计转速与实际转速偏差

估计扩展反电动势波形如图8所示，转速切换瞬间出现一个尖峰，但很快会跟随转速变化，因此不会影响到电机的动态性能。

图8　估计扩展反电动势

转子估计位置与实际位置波形如图9所示，可以看出估计转子位置能够很好地跟随实际转子位置，具有良好的估计效果。此外，由图10可看出，无论低速和高速运行，在稳态时估计转子位置和实际转子位置的偏差均在2°以内，实现了比较准确的转子位置估计。

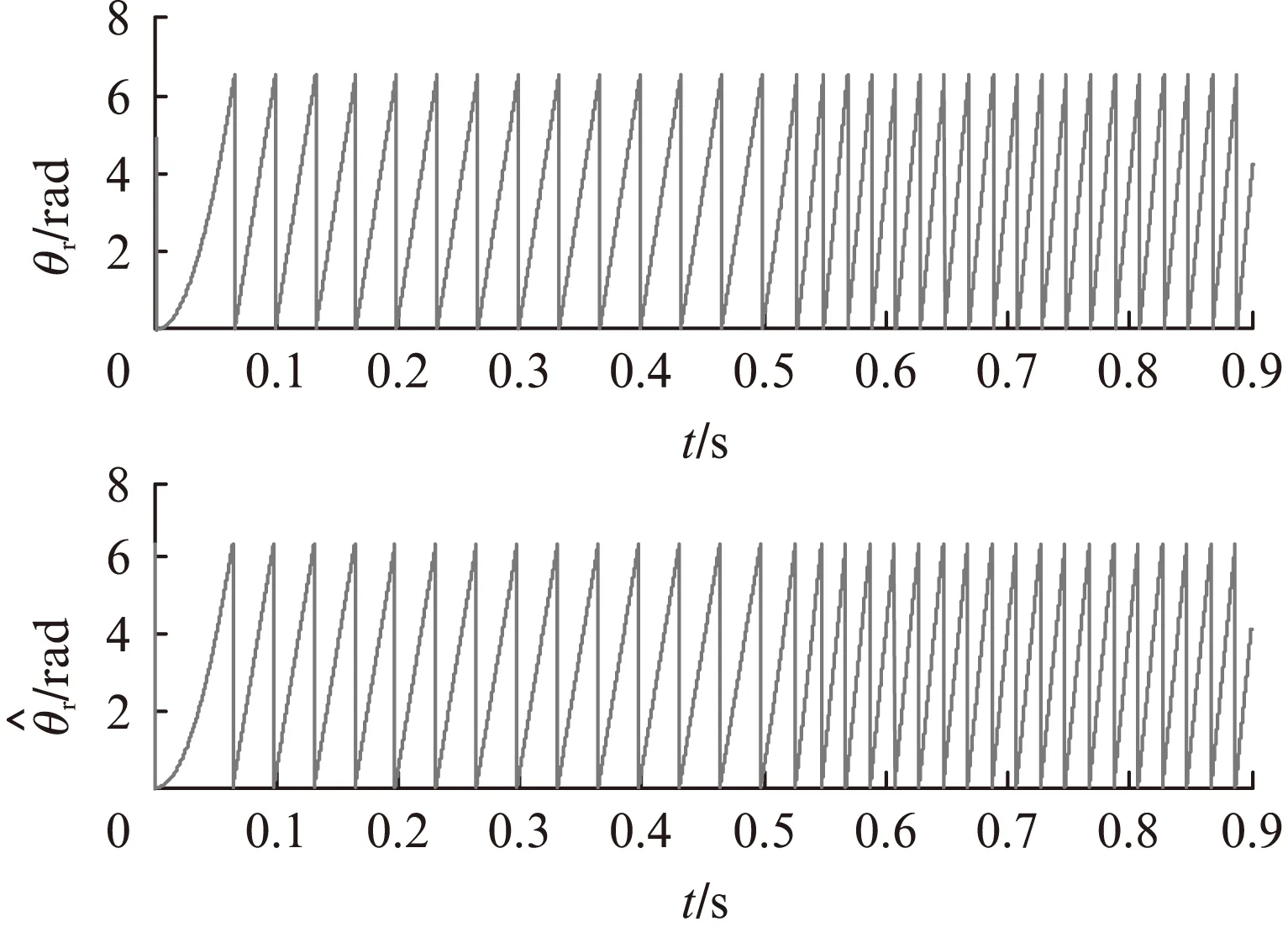
图9　转子实际θr和估计位置r

图10　转子位置角度偏差

5　结　语

本文采用SMO对扩展反电动势进行观测，通过选择适当的滑模增益以克服系统不确定性和参数变化的影响，采用扩展龙贝格观测器获得了电机转子速度和位置。仿真结果表明，所提出的方

法能够在不需要转子位置补偿条件下有效实现转子速度和位置的零相位滞后估计，系统具有良好的动、静态性能，是一种实现交流伺服系统无传感器运行的实用方法。

[1]陈亚爱，陈成，周京华.永磁同步电机转子位置检测技术[J].电机与控制应用，2013，40(7)： 47-52.

[2]刘毅，贺益康，秦峰，等.基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究[J].中国电机工程学报，2005,25(17)： 121-126.

[3]宋丹，吴春华，孙承波，等.基于滑模观测器的永磁同步电机控制系统研究[J].电力电子技术，2007，41(3)： 9-11.

[4]王高林，杨荣峰，于泳，等.内置式永磁同步电机无位置传感器控制[J].中国电机工程学报，2010，30(30)： 93-98.

[5]黄雷，赵光宙，年珩.基于扩展反电势估算的内插式永磁同步电动机无传感器控制[J].中国电机工程学报，2007，27(9)： 59-63.

[6]王丰尧.滑模变结构控制[M].北京： 机械工业出版社，1998.

[7]刘金琨.滑模变结构控制MATLAB仿真[M].2版.北京： 清华大学出版社，2012.

[8]SRIKANTH V， AMAR D. A comparative study on the effect of switching functions in SMO for PMSM drives[C]∥2012 IEEE International Conference on Power Electronics, Drives and Energy Systems，2012： 1-6.

[9]邱忠才，郭冀岭，肖建.基于Sigmoid函数的PMSM滑模变结构位置速度观测器[J].电气传动，2014，44(3)： 3-7.

[10]HYUNBAE K, MICHAEL C H, ROBERT D L. Sensorless control of interior permanent magnet machine drives with zero-phase lag position estimation[J]. IEEE Transactions on Industry Application， 2003,39(6)： 1726-1733.

Sensorless Control of AC Servo Motor Based on Sliding Mode Observer

GUOChaowei,GAOYanxia,ZHANGQuyao,SONGWenxiang

(School of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China)

A sensorless control method of permanent magnet synchronous AC servo motor based on sliding mode observer (SMO) was presented. Through the analysis for mathematical model of PMSM in static coordinate system, extended electromotive force (EEMF) estimation which contains traditional back EMF and a kind of voltage related to the saliency of the motor was introduced based on the sliding mode current observer, the sliding mode observer was constructed to estimate the EEMF component in two-phase static coordinate system. Analyzed the reasons of the existence of chattering, Sigmoid function was used to reduce the chattering, instead of constant switching function. Using extended Luenberger observer to observe the position and velocity of the rotor. Simulation results were provided to verify its feasibility and effectiveness.

AC servo motor; sensorless control; sliding mode observer; extended Luenberger observer

国家重大科学仪器设备开发专项资助项目(2012YQ15008703)

TM 383.4+2

A

1673-6540(2015)04-0001-05