铵根离子在水溶液中的跳跃转动机理

2015-09-03赵东霞

物理化学学报 2015年8期

关键词：化学系水溶液氢键

张强程程张霞赵东霞

(1渤海大学化学系,辽宁锦州 121000; 2辽宁师范大学化学系,辽宁大连 116029)

铵根离子在水溶液中的跳跃转动机理

张强1,*程程1张霞1赵东霞2

(1渤海大学化学系,辽宁锦州 121000;2辽宁师范大学化学系,辽宁大连 116029)

铵根离子的动力学行为与生命体内的生物和化学过程密切相关.依据流体力学理论,由于铵根离子与水分子之间存在多个强氢键,其转动应较慢,但实验结果并非如此,其转动的微观机理尚不清晰.本文分子动力学模拟研究表明,水溶液中铵根离子主要以快速、大角度的跳跃方式进行转动,像水分子一样遵从扩展分子跳跃转动模型.通过微观转动模式的分解和两种转动弛豫时间的比较发现,相对其氢键骨架的扩散转动,跳跃转动对其转动速率贡献更大,并随浓度增大不断强化.与水分子氢键交换方式相比,铵根离子更倾向于在非氢键相连的水分子间发生交换.

铵根离子; 跳跃转动; 氢键; 分子动力学模拟; 扩展跳跃模型

1 Introduction

Ions have significant impact on the structures and dynamics of water in aqueous solution,which have been extensively explored by the experimental and theoretical methods.1–10The rel-evant phenomena are brought into sharp focus in recent years,such as ion pairing5,6and ion specific effect on the biological systems.1,7–9In recent years,the ion disturbance on the motion of the water molecules has been extensively explored by the modern spectroscopy techniques3,4,10–13and the theoretical methods.14,15But the dynamic properties of ion itself in aqueous solutions are not well addressed at the microscopic level,for example ammonium ion.

The dynamics of ammonium ion and ammonium moieties plays an important role in the chemical,environmental,and biological processes.16–18Ammonium transport across the membranes is a crucial life-process for growth of plants,fungi,and bacteria.The transport mechanism of ammonium ion and ammonia in the protein channels of the ubiquitous ammonium transporter/methylamine permease/rhesus(Amt/MEP/Rh) family is far from understood.18The previous measurements of the nuclear magnetic resonance(NMR) suggested that the observed solvent dependence of the rotational mobility of ammonium ion showed a poor correlation with the hydrodynamic Stokes-Einstein-Debye(SED) model.19–23There is stronger short-range friction between ammonium ion and water due to the multiple strong hydrogen bonds(HBs) than that between ammonium ion and methanol.However,rotates rather fast in aqueous solutions comparing to that in other solvents such as methanol.This is unexpected for the hydrodynamic theories.The further simulations with the classical,non-additive,and electronic structure methods show that a discontinuous jump rotation possibly contributes to this unexpected fast rotation in aqueous solution.23–31However,the rotational mechanism of ammonium ion at the molecular level,is not well clarified intuitively and quantitatively until now.

The extended jump model(EJM) developed from Ivanov jump model,32,33shows that the rotation of water in aqueous solutions is determined by a large-amplitude angular jump and a less significant diffusive “frame diffusion”.14,15,32,33It has been applied to explore the rotational mechanism of water in the electrolyte solutions and on the hydrophobic interfaces combined with infrared(IR) spectroscopy and molecular dynamics simulations.32

In this work,the fast rotation ofin previous experiments was also observed in our simulations.The rotation of ammonium ion in NH4Cl aqueous solutions also follows the EJM like water molecule.It is mainly due to the large-amplitude angular jump during the HB switching processes offrom one acceptor to another in aqueous solutions.Two characteristic jump angles observed in our simulations are 50° and 65° for water and ammonium ion,respectively.Water prefers the former over the later,but conversely for ammonium ion.

2 Methods

2.1 Rotational correlation function

The rotational correlation function,C2(t),of water along OH bond vector oralong NH bond vector,u,can be expressed as:

where P2is the second-rank Legendre polynomial.C2(t) is usually employed to obtain the rotational relaxation time in simulations,which corresponds to the NMR and the ultrafast IR spectrum measurements.32The rotational correlation functions can be decomposed into two sub-processes(Fig.1),a short-time libration and a long-time rotational relaxation.The rotational relaxation times of two processes can be approximately obtained by fitting the following function:

where A is a prefactor of the exponential functions.τ1is the librational time.τ2is the rotational relaxation time related to the measurements of the ultrafast IR spectrum.4,12,13,32The integration value of C2(t) within a long-time window is usually used for the rotational relaxation time by NMR measurements.The parameters in Eq.(2),τ1and τ2were determined from a fit of equation(2) within 0–8 ps as previous works.4,12,13,32

Fig.1 Rotation correlation functions(C(t)),the HB correlation functions(1―CW-W(t)) and the rotation correlation functions of HB frame(Cf(t)) of the water and ammonium for the HB exchange between water molecules in NH4Cl solution at 0.5 mol·L–1

2.2 Extended jump model

The jump rotation of water or ammonium is triggered by the HB switching from initial HB acceptor to a new one(Fig.2).32Before a HB exchange(t ＜ 0 for the time window of the HB exchange process),O*H*or N*H*rotates diffusively with its HB frame axis of O*···Oaor N*···Oa.The average direction is assumed to be the same as the frame axis,neglecting the libra-tion of O*H*or N*H*in local HB frame axis.When a new HB acceptor is available,a fast HB switching happens.H*jumps from initial acceptor to a new one within the local frame of OaO*Obor OaN*Ob(Fig.2,Oaand Ob:the HB initial and final acceptors(oxygen atoms of water);H*:the HB donating hydrogen).When a new HB forms,the time window of the HB exchange process takes at t ＞ 0.The middle time between the ending moment of old HB and the beginning time of new HB,is taken as the time origin(t=0) within the HB exchange process.The jump angle φ is the angle between initial HB frame vector and the new HB frame vector at t=0(Fig.2).

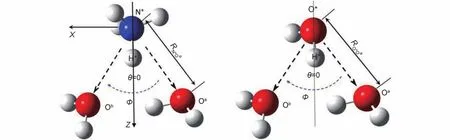
Fig.2 Definitions of the geometric variables along the HB exchange path

Based on the assumptions above,the rotational correlation function of molecule along the vector u(O*H*and N*H*bond vectors for water and ammonium ion,respectively),C2(t),can be further decomposed into two sub-processes after an initial fast libration decay(Fig.2):32(1) a sudden large-amplitude angular jump rotation of uv(uvis the O*H*or N*H*bond vector within the local HB frame uf,which is the O*···Oaor N*···Oavector of HB pair) and(2) a slow diffusive rotation of the frame vector uf.The correlation functions of two sub-processes(a jump rotational correlation function CJ(t) and a frame rotational correlation function Cf(t)) are both assumed to be exponential.

In NH4Cl aqueous solutions,the possible HB donors are the hydrogen atoms of water and.The possible HB acceptors are the water oxygen and chloride ion.Four HB exchange processes can be defined according to the types of initial and final HB acceptors:from water to water(W-W),from water to Cl–(W-Cl),from Cl–to water(Cl-W),and from Cl–to Cl–(Cl-Cl).The HB exchange can be traced along the trajectories of simuθH*O*Ob＜ 30° for water-water HB as previous work,32RO*Oalations,if the HB criteria are defined.The HB criteria:RO*Oa(RO*Ob) ＜ 0.350 nm,RH*Oa(RH*Ob) ＜ 0.245 nm and the HB angle(RO*Ob) ＜ 0.345 nm,RH*Oa(RH*Oa) ＜ 0.235 nm and the angle θH*O*Ob＜ 30° for the-water HB according to the radial distribution functions.34Rijis the distance between two atoms i and j of two HB connected molecules.θH*O*Obis the angle between the vectors O*H*and O*Ob.

For a HB exchange of O*H*or N*H*from initial acceptor i to new acceptor j(Fig.2),the rotational relaxation time τi-jaccording to Eq.(3),can be written as

Ai-jandare the fraction and the rotational time of O*H*or N*H*with an initial acceptor i and a final acceptor j.

According to the Ivanov model,33the jump rotational relaxation timeis derived from

fi-j(φi-j) is a function of jump angle φi-jdefined in Fig.2.φi-jis the average value of jump angle during the HB exchange from initial HB acceptor i to final acceptor j.The jump angle has a unsymmetrical distribution around the average value,32so a numerical integration value Fi-j(φ) over φi-jfrom 0 to π,is adopted in this work instead of the average value in previous work,32

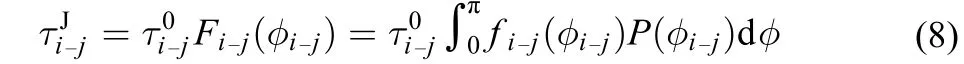
P(φi–j) is the possibility of the HB exchange from i to j with jump angle φ.32

2.3 Simulation protocol

The cubic bulks were constructed for pure water and NH4Cl aqueous solutions by inserting the water and ions into the empty box randomly,then the simulations were performed.2000 waters were filled into each sample box,thenand Cl–were inserted into the box until the concentration of solution is approximately equal to 0.5,1,2,and 5 mol·L–1.The SPC/E water model35was used and ammonium force field was taken from the previous publication by Jungwirth and his workfellows(Model I).34In their work,the properties,such as the solvation structures,ion clustering tendency in ammonium halide aqueous solutions,were well presented with the current combined potentials in this work.34Another force field of ammonium(Model II)26was used to explore the effect of force field in simulations on the rotation of ammonium ion.The jump behaviors of ammonium ion and water are similar for two models(see Section 3.1).A little shorter HB relaxation time is observed for Model II than that for Model I.Additionally,previous work suggests that a classical force field is sufficient for the jump rotation behavior of water.14The jump rotation was also found in ab initio simulations.28,29The quantum effect on the rotation of ammonium ion should be further discussed,but the rotational mechanism of ammonium ion is expected to be not changed.

The bond lengths and angles of water andwere fixed at the equilibrium values by the SHAKE algorithm.36The Lorentz-Berthelot combination rules37were used for the Lennard-Jones interactions.For each sample,a 2 ns isothermal-isobaric ensemble(NPT) equilibration simulation was carried out to generate the proper size of the simulation box,followed by a 2 ns microcanonical ensemble(NVE) simulation to calculate the dynamic properties.For each NPT simulation,the bulk systems were weakly coupled to a bath with the Nose-Hoover thermostats38,39at the goal temperature with the relaxation time of 0.1 ps.The weak coupling Berendsen scheme was used to control the system pressure at 1.01×105Pa with the coupling time constant of 1 ps.40The equations of motion were integrated using the velocity Verlet integration scheme37and a time step of 2 fs.The long-range Coulombic forces were calculated using the particle-mesh Ewald method.41The non-bonded van der Waals interactions were truncated at 1.2 nm using the switching functions.Minimum image conditions were used.37The simulation configures were saved every 20 fs.All simulations were performed with the Tinker simulation code.42

3 Results and discussion

3.1 Jump rotation of

The rotational diffusion constant DRcan be derived from the mean square displacements(MSDs) of the labeled molecule or ion in the solutions,according to the Einstein relation,43

According to the ideal diffusive fluid model,44the nth-rank rotational time of() along the NH vector would satisfy the relationship with the rotational diffusion constant DR,The ratios τ1/τ2and τ1/τ3should be equal to the constant values,3 and 6.However they are only 1.97 and 2.71 at 0.50 mol·L–1,which is much lower than the ideal constants.The similar case is also found for water with the values of 1.97 and 2.78.The rotation ofapparently does not follow the diffusive Brownian motion picture.44,45

Does ammonium ion also follow the EJM like water?32,33An instantaneous and large-amplitude angular jump of water is motivated by the HB exchanges.The HB exchange can be considered as a chemical reaction from the reactant state O*H*···Oato the product state O*H*···Ob.This process passes through an dangling or bifurcated HB state of O*H*,which is a transition state with a very short lifetime,much shorter than the stable single HB reactant and product states.32,33Indeed in the NH4Cl solution at 1 mol·L–1,a very fast decay of the HB state correlation function to the value below 0.1 is observed within 0.1 ps for ammonium ion hydrogen with the dangling,and bifurcated HBs comparing to the single HB state(Fig.3).The lifetime ofhydrogen with dangling HB state and bifurcated HBs is evidently shorter than those of water correspondingly.The facts above suggest that a transition state passes during the HB exchanges of ammonium ion like water molecule.

For ammonium ion,we can construct a similar HB exchange reaction system as water molecule.This exchange reaction systemis made of three molecules(ammonium ion,its initial and final HB acceptors).The configurations of remaining water molecules and ions in bulk solution are considered as the average background effect.The reaction coordinates of the HB exchange(Fig.2),which are the distance between N*and Oa(RN*Oa),the distance between N*and Ob(RN*Oa) and the angle(θ) between the N*H*bond and bisector plane of OaN*Ob,are analyzed from more than 250000 successful HB exchanging events.A·mong the possible HB exchanges in NH4Cl solution at 0.5 molL–1,the fraction of W-W HB exchange of N*H*(Fig.1) has the highest value,0.93(the definitions of HB exchange type in method part).

Fig.3 HB state correlation functions of the hydrogen atom of water and

Fig.4 Reaction coordinates Rij,θ,and φalong the path of the W-W HB exchange of ammonium ion and water

Fig.5 Jump angle populations of W-W HB switching for water and ion

An intuitive picture is presented in Fig.4 for the HB exchange reaction of ammonium.The departure of initial acceptor Oaand the arrival of new acceptor Obtake place cooperatively during the HB exchange process.A sudden and largeamplitude angular rotation of N*H*within the local HB frame of OaN*Obis observed at t=0.It is reasonable to assume that the local HB frame of OaN*Obdoes not change during the transient jump rotation of N*H*.32This is suggested by the value ofφ(definition in Fig.2),which nearly does not change during the W-W HB exchange(Fig.4).Jump angle populations of water andN H+4are shown in Fig.5.For water,a main peak locates at 50° and a shoulder peak at 65°.However,only one peak is visible at 65° for the jump angle of N H+4.The jump angle distribution of N H+4is almost symmetrical around the average value.The different features for the jump angles of water andNH+4suggest that the configurations at the transition state(t=0) are different.RN*Oaand RN*Obare not sensitive to the configuration of the transition state due to the strong HB interaction,so the jump angle is mainly determined by the distance(ROaOb) of HB acceptors,Oaand Ob.The possibility of jump angle at about 500 is much lower for ammonium ion than that for water,if a hydrogen bond is formed between the initial HB acceptor water and final HB acceptor water.The distances of N*···Oa,N*···Ob,and Oa···Ob,are about 0.31,0.31,and 0.28 nm for N*H*(Figs.2 and 4).The average jump angle at 65° is identified for both waterand ammonium ion for the HB exchange event without hydrogen bond between two HB acceptor water molecules at the transition 46 state.The distances of N*···Oa,N*···Ob,and Oa···Obare about 0.31,0.31,and 0.35 nm for anmonium ion,about 0.33,0.33,and 0.38 nm for the water.The possibility of the HB exchange between two HB water molecules without formation of HB each other,is higher for ammonium ion than that for water.This is mainly due to less available new HB acceptor around N*H*than O*H*.

3.2 Contributions from the jump and frame rotations

The rotational relaxation times of water and ammonium directly from equations(1,2) and from the EJM with equations(3)–(5),are presented in Fig.6.The tendency of the rotational relaxation times with concentration is well reproduced by the EJM.The rotational relaxation times are a little underestimated by the EJM relative to the direct measurements.The results from EJM suggest that the water rotation along the OH vector can be divided into two sub-processes.One is the large-amplitude and fast jump rotation.The other is the diffusive rotation of HB frame O*Oa.In NH4Cl solution at the lowest concentration(0.5 mol·L–1) of the samples in this work,the jump rotational times of water and ammonium ion are 3.81 and 4.57 ps,respectively.Their frame rotational times are 5.96 and 9.30 ps,respectively.The jump and diffusive rotational times rise to 7.30 and 18.59 ps at 5 mol·L–1.The contribution from the jump rotation to the rotational mobility of ammonium increases with concentration.The rotation time of ammonium ion and water is mainly determined by the jump rotation over the whole range of concentration.

As for the underestimation of the EJM,this is mainly due to the invalidation of its assumption and its intrinsic limitation.For the jump rotation,the average direction used in the EJM is assumed to be the same as the frame vector,neglecting the libration of O*H*or N*H*in local HB frame.The jump rotation term in fact covers a part of fast libration contribution in its long-time rotation contribution in equation(2).Additionally,the EJM does not consider the rotations of ammonium and water in local basins suggested in reference.50The fast HB exchange in local basin has bigger contribution on the fast decay of the rotational correlation function than the long-time decay.47A faster jump rotation is expected for the EJM,given its intrinsic limitations above.

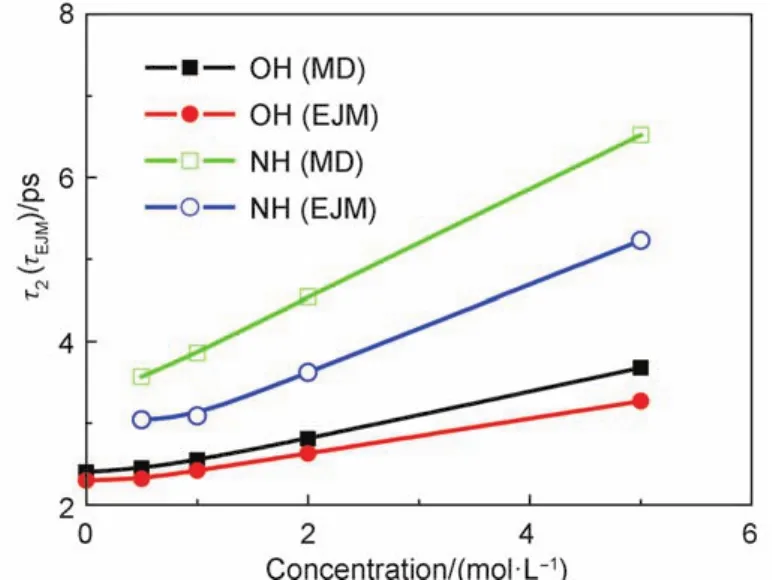
Fig.6 Rotational relaxation times of water and ammonium

4 Conclusions

The rotational mechanism of ammonium ion is explored by MD simulations and the extended jump model.The fast rotation of N H+4observed in previous experiments is due to the sudden jump rotation.The jump rotation of N H+4is motivated by the HB exchanges.The rotational behavior can be approximately described with the EJM like water in aqueous solutions.The rotational correlation function can be decomposed into a jump rotation and a diffuse rotation of HB frame based on the EJM.The contribution from the fast jump rotation is bigger than the diffusive part.The jump rotation becomes more and more important with concentration.Comparing to the HB exchange of water,the HB exchange of ammonium ion between two water molecules forming HB each other has a lower possibility than water.

(1)Nostro,P.L.;Ninham,B.W.Chem.Rev.2012,112,2286.doi:10.1021/cr200271j

(2)Marcus,Y.Chem.Rev.2009,109,1346.doi:10.1021/cr8003828

(3)Ohtaki,H.;Radnai,T.Chem.Rev.1993,93,1157.doi:10.1021/cr00019a014

(4)(a) Bakker,H.J.;Skinner,J.L.Chem.Rev.2010,110,1498.doi:10.1021/cr9001879(b) Bakker,H.J.Chem.Rev.2008,108,1456

(5)Marcus,Y.;Hefter,G.Chem.Rev.2006,106,4585.doi:10.1021/cr040087x

(6)Collins,K.D.Biophys.J.1997,72,65.doi:10.1016/S0006-3495(97)78647-8

(7)Mason,P.E.;Dempsey,C.E.;Vrbka,L.;Heyda,J.;Brady,J.W.;Jungwirth,P.J.Phys.Chem.B 2009,113,3227.

(8)(a) Yang,L.J.;Fan,Y.B.;Gao,Y.Q.J.Phys.Chem.B 2011,115,12456.doi:10.1021/jp207652h(b) Zhang,Q.;Xie,W.;Bian,H.;Gao,Y.Q.;Zheng,J.;Zhuang,W.J.Phys.Chem.B 2013,117,2992.

(9)Hofmeister,F.Arch.Exp.Pathol.Pharmakol.1888,24,247.doi:10.1016/j.orgel.2008.12.008

(10)Heisler,I.A.;Mazur,K.;Meech,S.R.J.Phys.Chem.B 2011,115,1863.doi:10.1007/BF01918191

(11)Engel,G.;Hertz,H.G.Ber.Bunsen.-Ges.Phys.Chem.1968,72,808.doi:10.1021/j100849a009

(12)Park,S.;Fayer,M.D.Proc.Natl.Acad.Sci.U.S.A.2007,104,16731.doi:10.1073/pnas.0707824104

(13)Roberts,S.T.;Ramasesha,K.;Tokmakoff,A.Accoutns Chem.Res.2009,42,1239.doi:10.1021/ar900088g

(14)Laage,D.;Hynes,J.T.Proc.Natl.Acad.Sci.U.S.A.2007,104,11167.doi:10.1073/pnas.0701699104

(15)Stirnemann,G.;Wernersson,E.;Jungwirth,P.;Laage,D.J.Am.Chem.Soc.2013,135,11824.doi:10.1021/ja405201s

(16)Moberg,R.;Bokman,F.;Bohman,O.;Siegbahn,H.O.G.J.Am.Chem.Soc.1991,113,3663.doi:10.1021/ja00010a005

(17)Anderson,T.L.;Charlson,A.J.;Schwartz,S.E.;Knutti,R.;Boucher,O.;Rodhe,H.;Heintzenberg,J.Science 2003,300,1103.doi:10.1126/science.1084777

(18)(a) Mason,P.E.;Heyda,J.;Fischer,H.E.;Jungwirth,P.J.Phys.Chem.B 2010,114,13853.doi:10.1021/jp104840g(b) Wang,S.;Orabi,E.A.;Baday,S.;Berne`che,S.;Lamoureux,G.J.Am.Chem.Soc.2012,134,10419.(c) Baday,S.;Wang,S.;Lamoureux,G.;Bernèche,S.Biochemistry 2013,52,7091.

(19)Perrin,C.L.;Gipe,R.K.J.Am.Chem.Soc.1986,108,1088.doi:10.1021/ja00265a044

(20)Perrin C.L.;Gipe,R.K.Science 1987,238,1393.doi:10.1126/science.238.4832.1393

(21)Masuda,Y.J.Phys.Chem.A 2001,105,2989.doi:10.1021/jp003300b

(22)Einstein,A.Investigations on the Theory of the Brownian Motion;Dover:New York,1956.

(23)Karim,O.A.;Haymet,A.D.J.J.Chem.Phys.1990,93,5961.doi:10.1063/1.459479

(24)(a) Chang,T.;Dang,L.X.J.Chem.Phys.2003,118,8813.(b) Dang,L.X.Chem.Phys.Lett.1993,213,541.

(25)Szasz,G.;Riede,W.O.;Heinzinger,K.Z.Naturforsch.A 1979,34,1083.

(26)Jorgensen,W.L.;Gao,J.J.Phys.Chem.1986,90,2174.doi:10.1021/j100401a037

(27)Jensen,K.P.;Jorgensen,W.L.J.Chem.Theory Comput.2006,2,1499.

(28)Bruge,F.;Bernasconi,M.;Parrinello,M.J.Am.Chem.Soc.1999,121,10883.doi:10.1021/ja990520y

(29)Bruge,F.;Bernasconi,M.;Parrinello,M.J.Chem.Phys.1999,110,4734.doi:10.1063/1.478360

(30)Kassab,E.;Evleth,E.M.;Hamou-Tahra,Z.D.J.Am.Chem.Soc.1990,112,103.doi:10.1021/ja00157a016

(31)Babiaczyk,W.I.;Bonella,S.;Guidoni,L.;Ciccotti,G.J.Phys.Chem.B 2010,114,15018.doi:10.1021/jp106282w

(32)(a) Laage,D.;Hynes,J.T.Science 2006,311,832.doi:10.1126/science.1122154(b) Laage,D.;Stirnemann,G.;Sterpone,F.;Hynes,J.T.Accoutns Chem.Res.2012,45,53.

(33)Ivanov,E.N.Sov.Phys.JETP 1964,18,1041.

(34)Heyda,J.;Lund,M.;Ončák,M.Slavíček,P.;Jungwirth,P.J.Phys.Chem.B 2010,114,10843.doi:10.1021/jp101393k

(35)Berendsen,H.J.C.;Grigera,J.R.;Straatsma,T.P.J.Phys.Chem.1987,91,6269.doi:10.1021/j100308a038

(36)Andersen,H.C.J.Comput.Phys.1983,52,24.doi:10.1016/0021-9991(83)90014-1

(37)Allen,M.P.;Tildesley,D.J.Computer Simulation of Liquids;Clarendon Press:Oxford,1987.

(38)Nosé,S.Mol.Phys.1984,52,255.doi:10.1080/00268978400101201

(39)Hoover,W.G.Phys.Rev.A 1985,31,1695.doi:10.1103/PhysRevA.31.1695

(40)Berendsen,H.J.C.;Postma,J.P.M.;van Gunsteren,W.F.;DiNola,A.;Hauk,J.R.J.Chem.Phys.1984,81,3684.doi:10.1063/1.448118

(41)Darden,T.;York,D.;Pedersen,L.J.Chem.Phys.1993,98,10089.doi:10.1063/1.464397

(42)Ponder,J.W.;Richards,F.M.J.Comput.Chem.1987,8,1016.

(43)Mazza,M.G.;Giovambattista,N.;Starr,F.W.;Stanley,H.E.;Phys.Rev.Lett.2006,96,057803.doi:10.1103/PhysRevLett.96.057803

(44)Hansen,J.P.;McDonald,I.R.Theory of Simple Liquids;Academic:London,1986.

(45)Zasetsky,A.Y.;Petelina,S.V.;Lyashchenko,A.K.;Lileev,A.S.J.Chem.Phys.2010,133,134502.doi:10.1063/1.3486174

(46)(a) Zhang,X.;Zhang,Q.;Zhao,D.Acta Chim.Sin.2012,70,365.[张霞,张强,赵东霞.化学学报,2012,70,365.](b) Zhang,X.;Zhang,Q.;Zhao,D.X.Acta Phys.-Chim.Sin.2011,27,2547. [张霞,张强,赵东霞.物理化学学报,2011,27,2547.] doi:10.3866/PKU.WHXB20111107

(47)Qvist,J.;Mattea,C.;Sunde,E.P.;Halleb,B.J.Chem.Phys.2012,136,204505.doi:10.1063/1.4720941

Jump Rotational Mechanism of Ammonium Ion in Aqueous Solutions

ZHANG Qiang1,*CHENG Cheng1ZHANG Xia1ZHAO Dong-Xia2
(1Department of Chemistry,Bohai University,Jinzhou 121000,Liaoning Province,P.R.China;
2Department of Chemistry,Liaoning Normal University,Dalian 116029,Liaoning Province,P.R.China)

The dynamic behavior of the ammonium ion is closely related to the biological and chemical processes of life.A fast rotation ofin aqueous solution has been observed in previous experiments,which is unexpected from hydrodynamic theories because of the multiple strong hydrogen bonds(HBs) between ammonium ion and water.The mechanism behind this rotation is still not well understood.The simulations in this work show that a sudden and large-magnitude angular jump rotation occurs during the hydrogen bond exchange processes of the ammonium ion like water.The rotation of the ammonium ion can be approximately described with the extended jump model,and can be decomposed into two independent contributions∶ the jump rotation and the diffusive rotation of the HB frame.The rotational mobility of the ammonium ion is determined by fast jump rotation compared with the slow diffusive rotation.In addition,the contribution of the jump rotation increases with increasingconcentration.Compared with water,prefers to exchange its HB between two water molecules without forming a HB each other.

Ammonium ion; Jump rotation; Hydrogen bond; Molecular dynamics simulation;Extended jump model

April 17,2015;Revised:May 28,2015;Published on Web:June 1,2015.

O641

icle]

10.3866/PKU.WHXB201506013 www.whxb.pku.edu.cn

*Corresponding author.Email:zhangqiang@bhu.edu.cn.

The project was supported by the Scientific Research Foundation for Returned Scholars,Ministry of Education of China(No.46) and National Natural Science Foundation of China(21473083).