基于已有信息的转移区域抽样可靠度数值模拟方法

房艳峰（浙江海洋学院海运与港航建筑工程学院，浙江舟山　316022）

基于已有信息的转移区域抽样可靠度数值模拟方法

房艳峰
（浙江海洋学院海运与港航建筑工程学院，浙江舟山316022）

对结构可靠度计算中的数值模拟方法进行了讨论，推导出模拟值方差的理论公式和影响因素。提出了一种可以降低模拟值方差、增加抽样效率的重要抽样方法——基于已有信息的转移抽样区域法。应用这种方法时，可只在包括失效区的且概率已知的某局部区域内抽样。在相同的抽样数量下，由于利用该区域的已知抽样概率作为已有信息，其模拟方差与直接抽样的比值小于1，且该比值随着抽样区的减小而减小，近似呈线性变化。该局部区域可取以原点为中心以结构可靠指标为半径的圆形区域外部空间。理论分析和模拟结果都表明，转移抽样区域法得到的模拟值方差与直接抽样法的比值，随结构可靠指标的增大而呈非线性降低。当可靠指标大于3时，这个比值可以降低到1/100以下。

可靠度；数值模拟；重要抽样；方差；区域

结构可靠度的研究始于20世纪初，标志是美国人FREUDENTHAL发表的“the safety of structrues”一文［1］直到1969年美国人Cornell提出在可靠度分析中应用直接与失效概率相联系的可靠指标β来衡量结构的可靠度，并建立一次二阶距理论［2］，该理论才收到工程界的重视。1971年加拿大人LIND提出将可靠指标转化为易于为工程所接受的分项系数的形式。推动了结构可靠度理论在设计规范中的应用［3］。工程结构可靠度的计算方法是可靠度理论中的研究课题之一［4］。由于多重积分带来的数学困难，现有的计算方法均为近似方法。工程上常采用一次二阶矩法［5］，其实质是在标准正态空间中，求得原点到极限状态面的距离作为可靠指标，原理是在该空间沿任一轴的边缘分布均为正态分布。缺点是当极限状态面是非线性时，特别是在设计验算点处非线性较高时，根据其相对原点或凸或凹，计算结果偏大或偏小，即计算结果是近似的［6］。随着计算机技术的发展，计算精度较高的数值模拟方法，Monte Carlo法越来越受到人们的重视，并成为结构可靠度分析和设计的一个重要组成部分［4］。此种方法的缺点是当抽样数量不是很大时，模拟值离散性较大，得不到可靠的结果。为提高抽样效率，人们研究出许多降低模拟方差，改善模拟精度的抽样技巧，如重要抽样法、相关抽样法、分层抽样法等［7，8］。SHINOZUKA［9］将重要抽样法引入到结构可靠度计算中，至今已被许多学者研究和改进［10］。此方法中，取抽样函数与原分布函数形式相同，抽样函数重心取由一次二阶矩法求得的设计验算点［11］。此方法也用于多失效模式的结构［12］。BUCHER［13］提出了自适应抽样法，用失效子样对原变量密度函数的一阶和二阶矩构造正态分布的抽样密度函数，此法得到的失效概率常常偏低。ANG［14］提出了核函数法，构造的密度函数非常接近最佳抽样函数，但用于形成核函数的失效子样必须来自直接Monte Carlo法，即失效概率较小时不适用。金伟良提出了将条件抽样和重要抽样相结合的改进模拟方法［15］，进一步提高了模拟的抽样效率。贡金鑫提出一种新的方向重要抽样法［16］，该方法构造以验算点为中心的椭球抽样空间，将以验算点为中心的方向矢量变换为以坐标原点为中心的方向矢量来抽样，边优化边模拟，计算不复杂，却提高效率很多。张崎［6］提出一种基于Kriging模拟的重要抽样方法，此方法用Kriging模拟的高非线性极限状态方程来进行结构分析，大大减低了有限元分析时间。杨飞跃等提出了结构可靠度计算的特殊边缘区间抽样法，其基本思想是基于抽取的样本点大部分落在最大似然点附近且处于可靠域，只有少数远离最大似然点的特殊边缘区间抽样点才有可能落入失效域，故只对特殊边缘区间抽样点进行功能函数和示性函数的计算，以替代全局计算，从而提高抽样效率［17］。刘佩等首次对比分析了结构动力可靠度计算的三种重要抽样法，并对部分方法进行了补充修正。单元失效域法补充了依据随机数决定抽样区间的产生方法，根据单元失效域的条件概率和权重系数给出重要抽样密度函数。方差放大系数法直接通过激励过程的特性给出重要抽样密度函数的具体表达式［18］。KINGSTON等［19］在Monte Carlo中引入了有限元对几何复杂的、边界没有明确表达的极限状态方程，用人工神经网络方法构造响应面，并利用遗传算法进行了数值模拟，抽样效率高，精度好。RAJABALINEJAD等［20］提出了基于Bayesian思想的Monte Carlo结构可靠度模拟方法，将极限状态方程附近抽样点信息作为已知信息来提高模拟速度，此方法特别适用于动态边界的问题。ECHARD等［21］将Kriging模型与Monte Carlo数值模拟方法结合（AK-MCS方法），来提高结构可靠度的模拟速度。本文从模拟结果的方差入手，推导出模拟结果的方差计算公式，并借助重要抽样法原理，转移抽样区域，在此基础上提出新的抽样法——基于已有信息的转移区域抽样法。其方法是将包括失效区的抽样区域尽可能减小，跨越已知抽样概率的安全区域，获得了较高的模拟精度。

1　Monte Carlo法中的抽样原理

由于模拟结果结果相对比较精确，Monte Carlo法（又称数值模拟法）的模拟结果，可作为其它近似计算结果精度的检验和校核［4］。当样本数取得无穷大时，Monte Carlo法的模拟结果无限接近解析解。其理论依据为大数定律［22］。如果已知随机变量x的密度函数为fx（x）和分布函数Fx（x），根据失效概率的定义，可进行下面的公式推导

公式（1）中，pf表示结构的失效概率，Df表示失效域，f（x）为随机变量的密度函数。I［x］为示性函数，当功能函数x≤0时，示性函数I［x］=1，反之，I［x］=0。从公式（1）中可以看出，结构失效概率即极限状态方程所对应示性函数的数学期望。设U是单位均匀分布的随机变量。则y=FX-1（u）是与x具有相同分布的随机变量［23］。设随机变量y=（y1，y2，L，yn）是抽到的容量为N的一个样本，由于失效概率可表示为极限状态方程对应示性函数I［g（x）］的数学期望，而样本平均值又是失效概率的无偏估计。这样失效概率的估计值可表示为

图1　抽样点分布图（N=1 000）Fig.1　Distribution of sampling points （N=1 000）

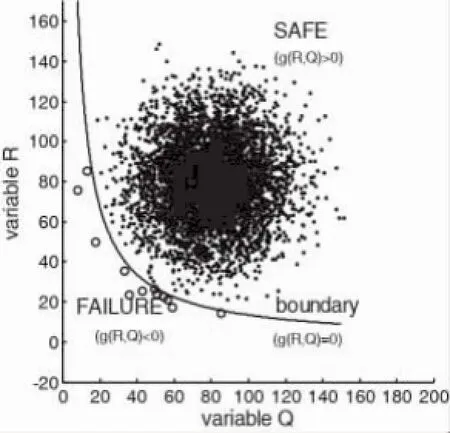
图2　抽样点分布图（N=5 000）Fig.2　Distribution of sampling points （N=5 000）

图3　数值模拟结果的对比分析Fig.3　Contrast and analysis of simulation results

2　利用已有信息的抽样区域转换法

在可靠度分析中，由于可靠度数值模拟的结果实质是样本均值，是一个随机变量。其波动性可用方差来表示为公式（3）

公式中D（pˆf）表示模拟值的方差，其他符号同前。从公式（3）可看出，随着抽样数量的增加，模拟结果的方差逐渐减小。这与图3的模拟结果相符。当数学期望不同时，模拟结果的集中程度可以用变异性来表示。用公式（4）来表达为

公式（4）中，δ（pˆf）表示模拟结果的变异系数。为增加数值模拟的精度，减少变异性，本文引入条件概率思想，通过转移抽样区域进一步加强模拟结果的稳定性。

图4　概率空间划分分析Fig.4　Space division of probability space

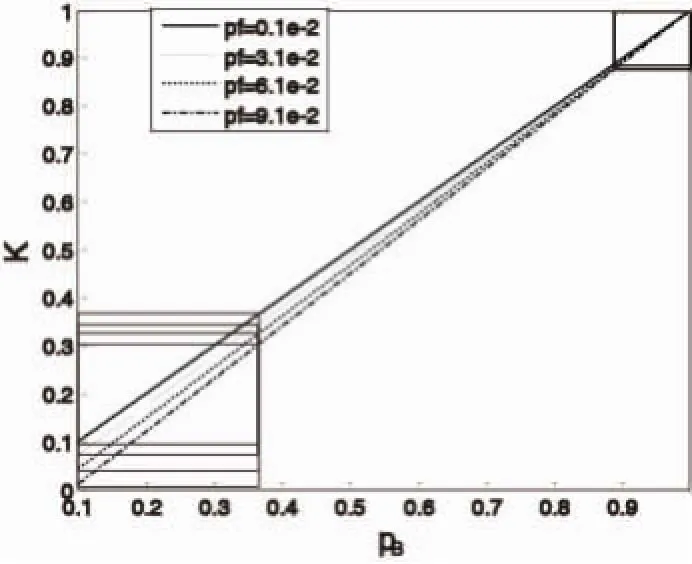
图5　比值K与pB的关系曲线Fig.5　Relationship btween ratio K and pB

图4表示抽样点的概率空间分成A和B两部分，失效区域位于空间B。如果抽样点落入空间A和B的概率p（A）=pA和p（B）=pB已知，则根据全概率公式，结构的失效概率可表示为

模拟结果的期望和方差分别为

显然抽样区域的分布概率pB是关键。图5表示，当结构失效概率pf在1e-3和9.1e-2之间时，方差比值k与pB的关系。转换抽样区域后的模拟方差随着pB的减小而减小，基本成线性关系。当pB固定时，方差缩减的程度随pf的增加而增加。这种增加的趋势随pB的增大而减小。即在pB较大时，方差缩减的程度对pf不敏感。例如，当pB=1.0，方差不缩减，即对任意值的pf，都有k=1。当pB=0.1时，pf从1e-3增加到9.1e-2，k从0.099 1降低到0.009 9。方差变化近10倍。

图6　概率空间划分分析Fig.6　space division of probability space

对于随机变量服从正态分布的可靠度计算问题，可以利用上述思想。将概率空间分为已知概率的安全区域A和未知概率的包含失效区域的区域B，如图6所示。图中的黑点和圆圈表示有限抽样点在整个概率空间中的模拟分布。A区域是以原点为中心以结构可靠指标为半径的圆。B区域是除A以外的概率空间，其包含失效区域FAILURE。由于正态分布的优良性［28］，的解析解易得。根据概率论中的3原则，是一微量。根据图5，数值模拟的方差可以缩减到直接模拟法的1/10以下，结果能够令人满意。

3　算例分析

3.1算例一

已知某结构的极限状态方程为fw-1365=0，随机变量f、w均服从正态分布，其参数见表1。分别利用直接Monte Carlo法和本文提出的基于已有信息的转移抽样区域法求得失效概率并比较收敛情况。

表1　随机变量的统计参数Tab.1　Parameters of random variables

Danny Shapiro先生：我们的汽车客户包括了宝马、本田和大众等。这些主机厂教会了英伟达应该如何针对汽车及使用环境进行产品设计，比如为汽车设计的芯片就必须经受粉尘、剧烈振动和极端温度等恶劣环境的考验。很难想象在笔记本电脑和PC机的芯片设计中会遇到这样的严酷条件。

经标准正态化后的极限状态方程为

本例题的解析解为=8.237e-4，pB=0.064。图7表示使用本文推荐方法后抽样点的分布情况。抽样点只分布在以结构可靠指标β为半径的圆形区域以外，可靠指标通过一次二阶矩求得，圆形区域内分布概率已知，并且此区不出现失效情况。结构失效概率可以由以下两式得出

公式中β表示由一次二阶矩法求得的可靠指标，x21-pB（2）表示卡方分布的分位点，其他符号意义同前。为了比较此方法的优越性，将直接Monte Carlo方法（simulation 1）和转移抽样区域法（simulation 2）的模拟方法结果分别用黑点和圆圈表示，以模拟值为横坐标，以抽样数量为纵坐标绘于图8中。抽样次数从10 000增到50 000，步长10 000。在同样抽样次数下，进行30次模拟，得到30个结果列在图上。可以看出，随抽样次数的增加，数值模拟的分散程度减小，但不显著，例如当抽样数从10 000增加到5 000，增加了5倍，模拟结果的分布范围值减少到原来的0.5倍。所以依靠增加抽样次数来达到减少方差的目的并不明智。相比之下，用本文的方法进行数值模拟，在抽样数量不多的情况下，模拟解的稳定性很好。模拟结果的分布区间长度大约是直接法的1/20。分散区域非常集中，模拟值可靠，没有较大偏差，精确度较高。图9和图10分别表示了采用直接模拟法和本文转换抽样区域法，随着抽样数目的增加模拟结果的方差变化情况。抽样次数从10 000增加到100 000，在每次确定的抽样次数下，模拟出300个结果并求其样本方差。从模拟结果来看，使用两种方法得到的模拟结果，样本方差随抽样次数增多而降低的趋势完全相同，即比值是一个常数，这和理论分析公式（3）和（8）完全吻合。

图7　抽样点分布（N=1000）Fig.7　Distribution of sampling points

图8　模拟结果分布和对比分析Fig.8　Contrast and Analysis of simulation results

图9　直接抽样法模拟方差与抽样次数关系Fig.9　Relationship btween variance from direct simulation and sampling number

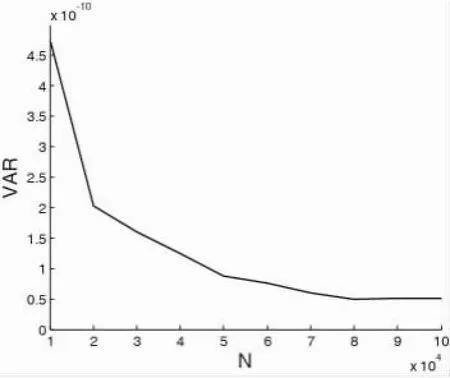
图10　转换区域法模拟方差与抽样次数关系Fig.10　Relationship btween variance from transfer regionmethod and sampling number

设结构的极限状态方程为线性，pf=1-Φ-（β），pB=1-chi2cdf（β2，2），结合方程（9）可以得到

公式（14）中，normcdf（·）是MATLAB软件中表达的标准正态分布函数，chi2cdf（·，2）表示二维卡方分布函数。图11表示使用区域法前后模拟方差之比与结构可靠指标之间的关系。从图上看出，随可靠指标β的增大，即随着失效概率pf的减小，方差的比值迅速增大。即结构的失效概率越小，用转移区域方法进行模拟优势越大，效果更为显著。当β=3时，使用区域法后的模拟方差可缩减到原来的1/100，β=3.5时，方差可缩减到原来的1/500。

图11　转换区域法模拟结果方差与可靠指标β关系Fig.11　relationship btween variance of simulation results by transfer region method and index β

3.2算例二

已知某结构的极限状态方程为，随机变量、均服从正态分布，其参数见表2。分别利用直接Monte Carlo法和本文提出的基于已有信息的转移抽样区域法求得失效概率并比较收敛情况。

表2　随机变量的统计参数Tab.2　Parameters of random variables

经标准正态化后的极限状态方程为

本例题的解析解为pf=0.014 95，pB=0.082 1。图12表示使用本文推荐方法后抽样点的分布情况。图13将直接Monte Carlo方法（simulation 1）和转移抽样区域法（simulation 2）的模拟方法结果分别用黑点和圆圈表示。图中的横坐标是模拟值，纵坐标是抽样次数。在相同抽样次数下，与直接模拟法（simulation 1）相比，转移抽样区域法（simulation 2）模拟结果的分散程度明显减小，但减小的幅度不如图8显示的强烈，那是本例题中结构失效概率较大，这个结论与图11所示相符。

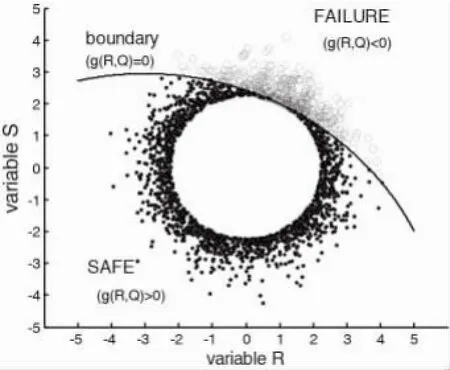
图12　抽样点分布（N=1 000）Fig.12　Distribution of sampling points

图13　模拟结果分布和对比分析（N=1 000）Fig.13　Contrast and Analysis of simulation results

3.3算例三

已知某结构的极限状态方程为，随机变量、均服从正态分布，服从对数正态分布。其参数见表3。设，经标准状态化后，分别利用直接Monte Carlo法和本文提出的基于已有信息的转移抽样区域法求得失效概率并比较收敛情况。本例中，由一次二阶矩法求得，。

表3　随机变量的统计参数Tab.3　Parameters of random variables

标准正态化后的方程为

本例题的解析解为pf=0.0255，pB=0.3068。图14、图15表示使用直接抽样（simulation 1）和本文推荐方法（simulation 2）后抽样点的分布情况。图16表示两种方法的模拟结果对比分析。在相同抽样次数下，与直接模拟法（simulation 1）相比，转移抽样区域法（simulation 2）模拟结果的分散程度减小，但不是很显著，因为本例题的失效概率较小。这个结论进一步证明图11的正确性。

图14　抽样点分布（N=1 000）Fig.14　Distribution of sampling points

图15　抽样点分布（N=1 000）Fig.15　Distribution of sampling points

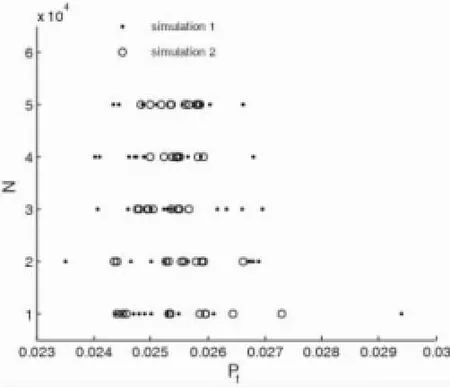
图16　模拟结果分布和对比分析Fig.16　Contrast and Analysis of simulation results

4　结论

本文所采用的转换抽样区域法基于Monte Carlo重要抽样法原理，通过转移抽样区域的方法来达到提高抽样效率的目的，证明时采用了全概率公式。跨过已知概率解析解的安全区域，只在此外的概率空间中求解，极大提高了抽样效率。原因是在模拟中融入了解析部分。模拟结果和理论分析表明，通过增加抽样次数而达到缩小模拟值方差的目的不能达到理想的效果，速度较慢。使用本文提出的模拟方法，数值解的波动性很小，方差减小的幅度很大。与直接抽样方差的比值，随着抽样区域的减小而减小，基本呈线性关系。它随结构可靠指标的增大而减小。当结构可靠指标β＞3时，模拟方差可以缩减到原来的1/100。即可靠指标越大，采用本文的抽样方法效果越显著。

［1］FREUDENTHAL A M.The safety of structures，Trans［Z］.ASCE，1947：112.

［2］CORNELL C A.A probability-based structural code［J］.ACIJ，1969，66（12）：974-985.

［3］LIND N C.Consistent partial safety factors［J］.J Struct Div，ASCE.97（ST6），1971：1 651-1 699.

［4］赵国藩.工程结构可靠性理论［M］.大连：大连理工大学出版社，1996.

［5］中华人民共和国国家标准.GB50153-92工程结构可靠度设计统一标准［S］.北京：中国计划出版社，1992.

［6］张崎，李兴斯.结构可靠性分析的模拟重要抽样法［J］.工程力学，2007，24（1）：33-36.

［7］RUBINSTEIN R Y.Simulation and the Monte Carlo Method［M］.New York：Wiley，1987.

［8］LEMAIRE M.Structural reliability［M］.New York：John Wiley&Sons，Inc，2009.

［9］SHINOZUKA M.Basic analysis of structural safety［J］.J Struct Eng，ASCE，1983，109（3）：721-740.

［10］ENGELUND S，RACKWITZ R.A benchmark study on importance sampling techniques in structural reliability［J］.Structural safety，1993，12：255-276.

［11］BOURGUND U，BUCHER C G.Importance Sampling Procedure Using Design Pionts（ISPUD）——.A user's Mannual［J］. Austria：Univ.of Innosbruck，1986.

［12］SHUELLER G I，STIX R.A critical appraisal of methods to determine failure probabilities［J］.Struct Safety，1987，4：293-309.

［13］BUCHER C G.A daptive sampling——an interative fast Monte Carlo procedure［J］.Struct Safety，1988，5：119-126.

［14］ANG G L，ANG A H-S，TANG W H.Kernel Method in Importance Sampling Density Function Estimation［J］.Proc 5th ICOSSAR'89，1989：193-200.

［15］金伟良.结构可靠度数值模拟的新方法［J］.建筑结构学报，1996，17（3）：63-72.

［16］贡金鑫，何世钦，赵国藩.结构可靠性模拟的方向重要抽样法［J］.计算力学学报，2003，20（6）：655-661.

［17］杨飞跃，张建仁.结构可靠度分析的特殊边缘区间抽样法［J］.工程力学，2009，26（9）：56-60.

［18］刘佩，姚谦峰.采用重要抽样法的结构动力可靠度计算［J］.计算力学学报，2009，26（6）：851-855.

［19］KINGSTON G B，RAJABALINEJAD M，GOULDBY B P，et al.Computational intelligence methods for the efficient reliability analysisof complex flood defence structures［J］.Structural Safety，2011，33（1）：64-73.

［20］RAJABALINEJAD M，DEMIRBILEK Z.Bayesian Monte Carlo method for monotonic models applying the Generalized Beta distribution［J］.Engineering Failure Analysis，2011，18（4）：1 153-1 161.

［21］ECHARD B，GAYTON N，LEMAIRE M.AK-MCS：An active learning reliability method combining Kriging and Monte Carlo Simulation［J］.Structural Safety，2011，33（2）：145-154.

［22］ROBERT C P，CASELLA G.Monte Carlo Statistical Methods［M］.北京：世界图书出版公司，2009.

［23］肖刚，李天柁.系统可靠度分析中的模特卡罗方法［M］.北京：科学出版社，2003.

［24］AYYUB B M，HALDAR A.Practical structural reliability techniques［J］.Journal of Structural engineering，ASCE，1984，110 （8）：1 707-1 725.

［25］BJERAGER P.On computation methods for structural reliability analysis［J］.Structural Safety，1990，9：79-96.

［26］HARBITZ A.An efficient sampling method for probability of failure calculation［J］.Structural Safety，1986，3：109-115.

［27］SCHUELLER G I，et al.An efficient computational scheme to calculate structural failure probabilities［Z］//LIN Y K，SCHUELLER G I，eds.Stochastic Structural Mechanics（Lecture notes in engineering）.Springer Verlag，1989.

［28］CASELLA G，BERGER R.Statistical Inference［M］.北京：机械工业出版社，2010：102-104.

Structural Reliability Analysis by Transfer Region Method based on the Information Obtained

FANG Yan-feng （School of Maritime and Civil Engineering of Zhejiang Ocean University，Zhoushan316022，China）

In the paper，simulation for structural reliability is discussed thoroughly.The formula of simulation variance is deduced and analysis of influencing factors on the variance is given.A new sampling method——transfer sampling region method is given which can reduce the simulation variance and praise the sampling efficiency.In the method，sampling points only come from some region with known probability and where，the failure area is included entirely.The certain region is choose because the probability of sampling points come from here is obtained easily for simple geometry，and by the known information，the simulation can be approached efficiently.The ratio of the variance of simulation from the method to that of direct method is less than 1，and the value will decrease with the size of sampling region linearly.The outer space of the circle with the origin as center and the reliability index as radius can be choose as the certain sampling region. Analysis and simulation results show that the ratio of the variance of simulation from transfer sampling region method to that from direct method will decrease with the increasing of reliability index nonlinearly and it can be reduced to be less than 1/100 when the reliability is greaterr than 3.

reliability；simulation；importance sampling；variance；region

TU311.2

A

1008-830X（2015）04-0395-08

2015-01-02

浙江省教育厅项目（Y201018955）

房艳峰（1976-），男，辽宁铁岭人，讲师，硕士，研究方向：结构工程研究.E-mail：fyf20021976@126.com