基于单步协调控制的大型游乐场游客智能导览系统的建模与仿真

郑天翔

(暨南大学 深圳旅游学院，广东 深圳 518053)

一、引 言

如今比较大型的游乐场，如迪士尼乐园、欢乐谷等，因为园区太大游客在游玩过程中常常会在园区里多走弯路和重复路。虽然不少园区在入口处提供纸质版地图，但内容不翔实、不直观，很多仅是简单的位置信息，缺乏路径指引的作用。有时甚至误选了距离当前位置较远的游玩项目，或者即便找到了想玩的项目也会因为设施外排队人数过多、等待时间过长而不得不为节约时间而选择其他的项目。如此一来，不但浪费自己的时间，还容易造成园区拥堵。如何避免某些时刻游客在个别游乐设施(以下简称项目或设施)过于拥挤，而其他设施游客寥寥无几的情况发生，减少游客在寻找和等待上的游玩成本，是值得学者共同关注的问题。

智能导览系统的出现，为解决这一难题提供了有效的方法。目前，国内学者主要从排队论和时空分流导航管理技术两个视角对智能导览问题展开探讨。排队论是以运筹学作为基础，研究服务机构中排队问题的规律，在旅游学科领域的研究成果并不算多，这些研究的主要思想是:首先借助M/M/n排队理论建立数学模型，然后结合多目标线性规划的方法来求解方程。时空分流导航管理技术则以信息科学作为基础探讨游览路线优化问题，使游客在景区内均衡分布、有序交换，目前研究正处于初级阶段，涌现出一批有影响力的成果。相比之下，国外在智能导览的相关研究上开始得比较早，也比较成功。例如，虚拟排队服务被广泛应用于主题公园的开发和运营中，其中以Multi Motion主题公园管理系统和迪士尼的FASTPASS排队管理系统最具代表性，这类系统设计的方案是增加一条虚拟排队队列，能使游客花费相同的时间但多体验一个项目。国外研究的另一个分支则是游线设计(Tourist Trip Design Problems)，其中涉及游客行进路线的文献也有不少。

尽管在景区智能导览问题上，国外的研究手段和成果比较丰富，然而，国外景区及其游客游憩行为与我国存在较大差异，已有相关模型无法直接应用于我国景区的游客管理实践，因此寻求适合我国景区的游客智能导览系统很有必要。此外，已有文献大多从全路线协调控制方法对游客行进路线进行智能导览，也就是说，当游客进入景区时系统就为游客推荐一条合适的路线，游客按照这个行程参观。这样得到的固化路线难以适应动态变化的人潮流动，体现不出“流动性”和相关地域单元之间的旅游流联系。鉴于计算机仿真建模方法是研究游客游憩行为与游憩环境影响的重要前沿方法，本文针对大型游乐场游客智能导览系统的决策支持问题，提出一个单步协调控制的游憩方向决策模型，并通过算例仿真验证模型的优越性，旨在通过模型构建的行进路线把游客自动散布到不太拥挤的设施上，以达到智能导览的目的。

二、大型游乐场游客智能导览系统

基于单步协调控制的大型游乐场游客智能导览系统通过以下4个步骤构建:(1)问题分析与假设;(2)构建大型游乐场游客智能导览系统的模型;(3)建立择优选择机制的游憩方向决策算法;(4)模型仿真与验证。

(一)问题分析与假设

虽然目前客流拥堵现象较为严重的景区以风景名胜区、名胜古迹为主，但由于通常的人流协调思路是将游客协调看作一个规划或调度问题，而这些风景区或名胜古迹的不确定性因素较多，因此难以对模型作精确分析。相比之下，排队问题同样突出的大型游乐场，则更利于对游客建模，且能对模型进行简化，因此，本文以大型游乐场(以下简称游乐场或者景区)作为研究对象。与风景名胜区相比，大型游乐场具有如下的特点:

(1)游乐项目(游乐设施)的容量可以预先确定。游乐项目具有独占性，同一时刻可供游玩的人数相对固定。

(2)游乐项目的游览用时可以预先确定。游客在游乐项目上的停留时长相对固定，一般就是游乐项目运转一次的用时。

(3)游客会走回头路。相邻游乐项目之间距离不会太远，很多时候为了减少等待时间，同一路径游客会重复往返。

(二)智能导览系统模型

景区游客智能导览系统，是景区游客游憩行为仿真模型的其中一项应用，根据前人研究成果并对其进行简化，可以把模型分解为停留点(游乐设施)、道路和游客三个对象。

1．停留点

停留点指景区内使游客产生停留时间的地点，在本文意义下，就是游乐设施。停留点的属性包含其地理位置、时间表、状态以及游客人数等。根据上文假设，游客人数就是设施容量，等候游客人数则通过设施外排队人数来体现;时间表包含设施游览用时、设施开放时刻和设施关闭时刻等基础属性;状态是指设施处于空闲还是繁忙状态，表现为设施下次可提供服务时刻。其中，地理位置、时间表和设施容量可作为模型的已知条件;设施下次提供服务时刻和设施外排队等候人数，可以在仿真阶段借助算法采用的数据结构来间接求出，而在实际管理实践中通过位置感知技术获悉，本文不做具体分析。

2．道路

道路表示景区地理环境要素中的道路。道路与停留点之间的交互结构为网络型，在本文意义下表现为道路和停留点之间是否可达。另外，为简便起见，本文不考虑道路通行能力的限制。

3．游客

游客表示景区内的游客，具有编号和偏好等静态特征属性，和与游憩行为相关的游憩方向、游憩速度、景点停留时长、等待时间、步行时间等动态特征属性。游客偏好包含感兴趣项目(要参观的项目列表)、到达时刻和预计离开时刻等。本文假设，游客偏好在游客到达以后直接确定，即作为模型的输入;游憩速度本文作统一处理，即不考虑游客在行走速度上的差异性;景点停留时长就是游乐设施的游览用时。此外，感兴趣的项目没有游览先后顺序之分。

(1)游憩方向。游客完成一个停留点的游览后，都要对下一步要移动的方向进行决策。游客的方向决策与下一步可达停留点的属性相关，如时间表和状态等，也与自身的偏好和需要花费的等待时间相关。下文将对此构造一种详细设计。

(2)步行时间。指游客从一个停留点移动到另一个停留点所需要花费的时间。由于本文假设所有游客的游憩速度相同，因此，步行时间主要由停留点之间的道路长度决定。

(3)等待时间。指游客在景区某停留点所等待的时间段，如果停留点空闲，则等待时间为零。否则，等待时间与停留点的游览用时、排队等候人数、设施容量、下次可提供服务时刻相关。

(三)游憩方向决策算法

1．单步协调控制方法

与全路线协调控制相比，单步协调控制方法是指在游客游览过程中，系统利用当前客流信息和景区环境信息逐次为游客选择下一游览点，选择的依据是通过某种择优机制来决定。当每个游客在进入景区时，系统会为其编号并收集其个人偏好。在游客游览过程中，每当游客完成一个项目后，系统根据当前拥挤信息为游客决定下一个游览项目，即采用逐次单步的方式自动生成游客的参观路线。本文采用基于择优选择机制的策略为:首先计算出游客在所有尚未游览的项目中需要付出的代价，然后从中选择代价最小的一个，具体可参见下一节。这种选择机制能让游客尽可能地前往当前最空闲的项目。

2．决策算法设计

算法构造的关键在于，首先需要判断设施是处于开放还是关闭期间，其次需要区分空闲、繁忙、待开放、已关闭等状态。然后，计算若选择该设施作为下一个参观游览的项目的话，需要付出的代价(通过等待时间刻画)。最后，同时考虑步行到该设施所需的时间，还有是否超过游客预计逗留景区时间或超过景点开放期限，来进一步确定该设施是否纳入候选行列。表1展示了构建的算法。

表1 基于择优选择机制的游憩方向决策算法

三、仿真实验

以实验室虚拟景区为研究对象，应用BorlandC++Builder软件平台构建模型及其运行环境。采用虚拟的游客行为数据进行模型运行的参数标定与模型校核，并以此为仿真实验的参数输入值，分析研究对象的智能导览结果。

(一)实验算例

在算例中，我们假设大型游乐场一共有5个游乐设施(用 V1，…，V5表示)，1个门口(用Gate表示)。设施与设施、设施与门口之间的道路长度如表2所示。

(二)参数设定

将游客在景区的停留时段按照某时间粒度分成若干Tick，本文设定每个Tick为1秒。游客仅需要在进入景区或某个游乐设施游览完毕后，才进行下一步动作的决策，游客处于停留点的游览或排队期间以及在道路上行进期间，均不做决策。

(1)景点数据:各景点的地理位置如表2所示。所有设施容量统一设置为1。在景点的时间表属性上，所有设施的游览用时统一设置为20秒，至于设施的开始时刻和关闭时刻，设施V1、V2和V3跟随游乐场开放而开放，设施V4的开始时刻随机设为游乐场开放后1分54秒，持续时间为2分17秒，设施V5的开始时刻为游乐场开放后1分44秒，持续时间为2分30秒。

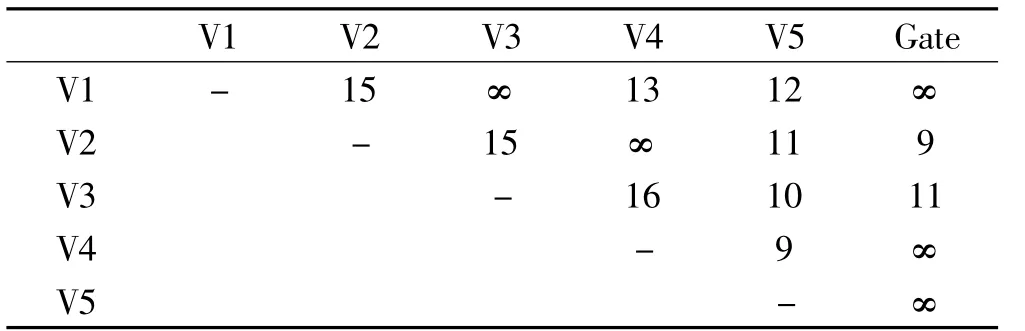
表2 各设施之间的道路长度

(2)游客数据:各游客的偏好(到达时刻、预计离开时刻和感兴趣的项目)参见表3。其中，到达时刻是指游乐场开放后的增量时间。游客的编号规则是按照其到达游乐场的时间先后依次进行编号的。

(三)验证结果

对应表3的游客数据，结合表2的景区空间地理位置图，通过仿真实验得到各停留点的排队等候人数和游客的实际等待时间，然后分析在三大评价指标下的导览效果。

1．游客等待时间

假如设施的游览人数太多，游客就需要排队等候，那么游客排队等候的时间长短就直接地反映了游客在景区游玩的效率，所以游客在游览期间等待时间的均值(即平均等待时间，等于总等待时间和要参观的项目数的比值)可以作为衡量模型优劣的基本指标。平均等待时间越小，则说明游玩效率越高。

从表4可以轻易计算出在本文模型下游客的平均等待时间为66.63秒，标准方差为14秒，说明各游客的等待时间差别不大，表明游客的等待时间基本不受其到达景区的时刻影响。此外，由于游客满意度是与等待时间占逗留时间的比例(以下简称等逗比)密切相关的，据此计算出本文模型下的等逗比如表4最后一列所示。可见，等逗比在各个游客上趋于平均(均值为0.4，标准方差为0.1)，表明所有游客的等逗比大体相同，不会因为到达先后的次序而有明显的差异。

2．设施利用率

设施利用率是衡量设施接待能力的重要指标，接待能力越强，则利用率越高。为此，把各停留点人数变动的时刻一一记录下来，也就是说，记录游客到达该设施开始游览或等候的时刻或在该设施上游玩结束离开景点的时刻，然后记下接待人次和统计等候人数。结果如表5所示。

由表5可知，设施V1－V5分别接待了9、9、11、7、7人次，由此可见各设施的接待能力大致相同，且各设施的负荷比较接近，排队等候人数峰值大概为3～4人。另一方面，从各列记录数量可间接反映出在本文模型的智能引导下，没有出现一部分设施有大量的容量剩余，而其他设施异常繁忙的情况。

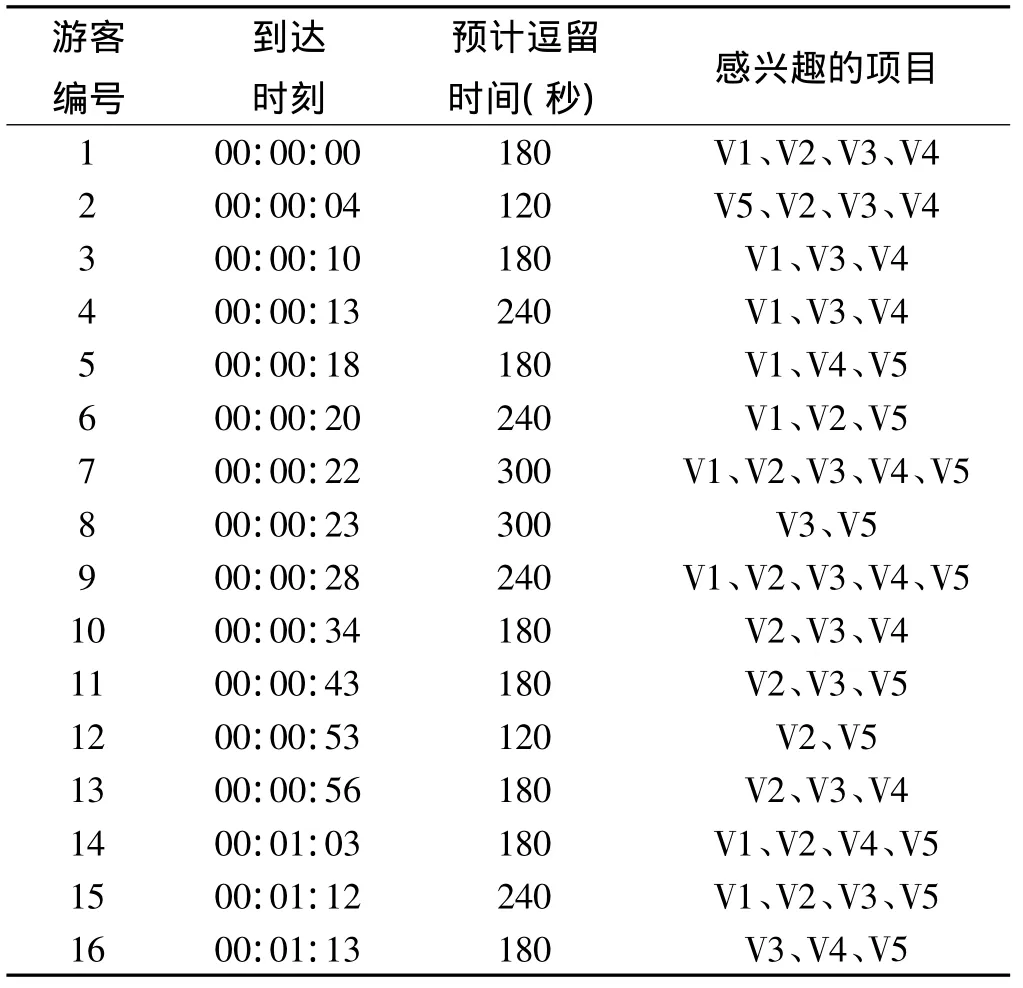
表3 游客数据

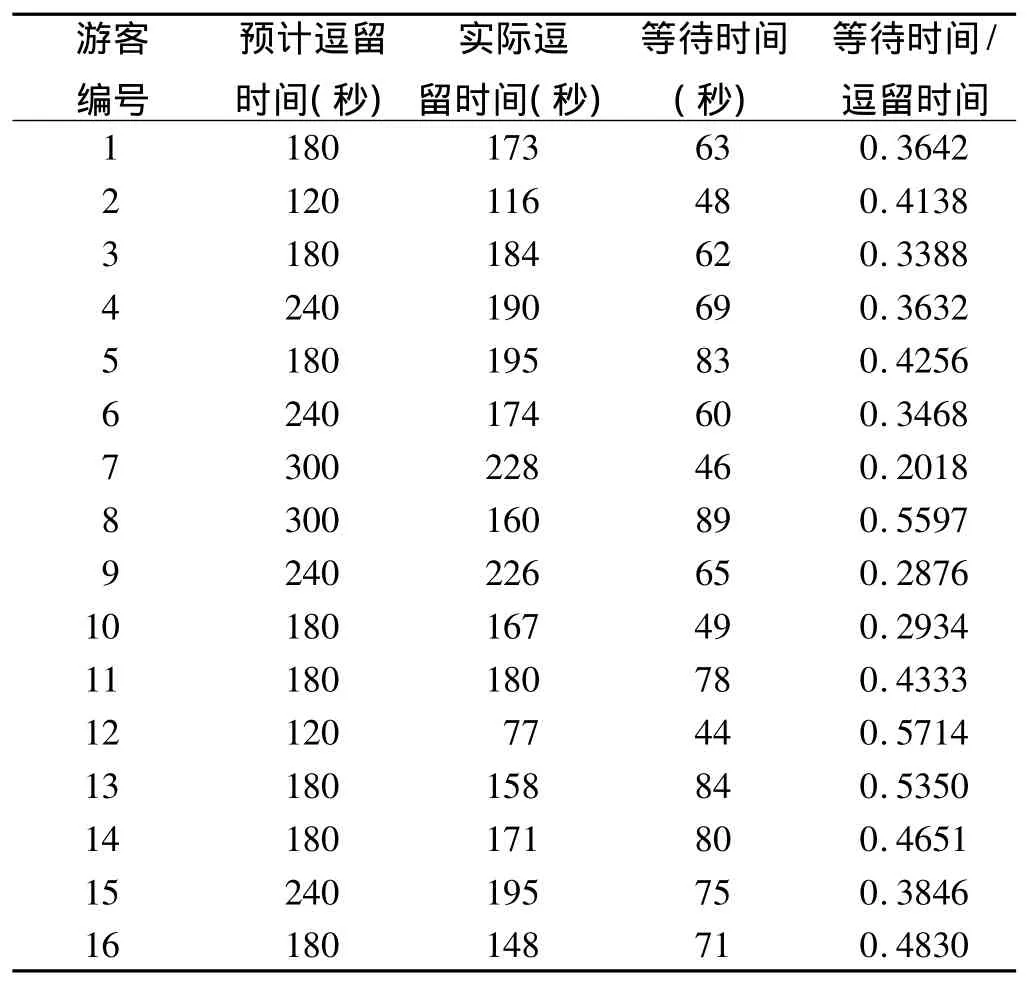
表4 本文模型在“游客等待时间”上的结果

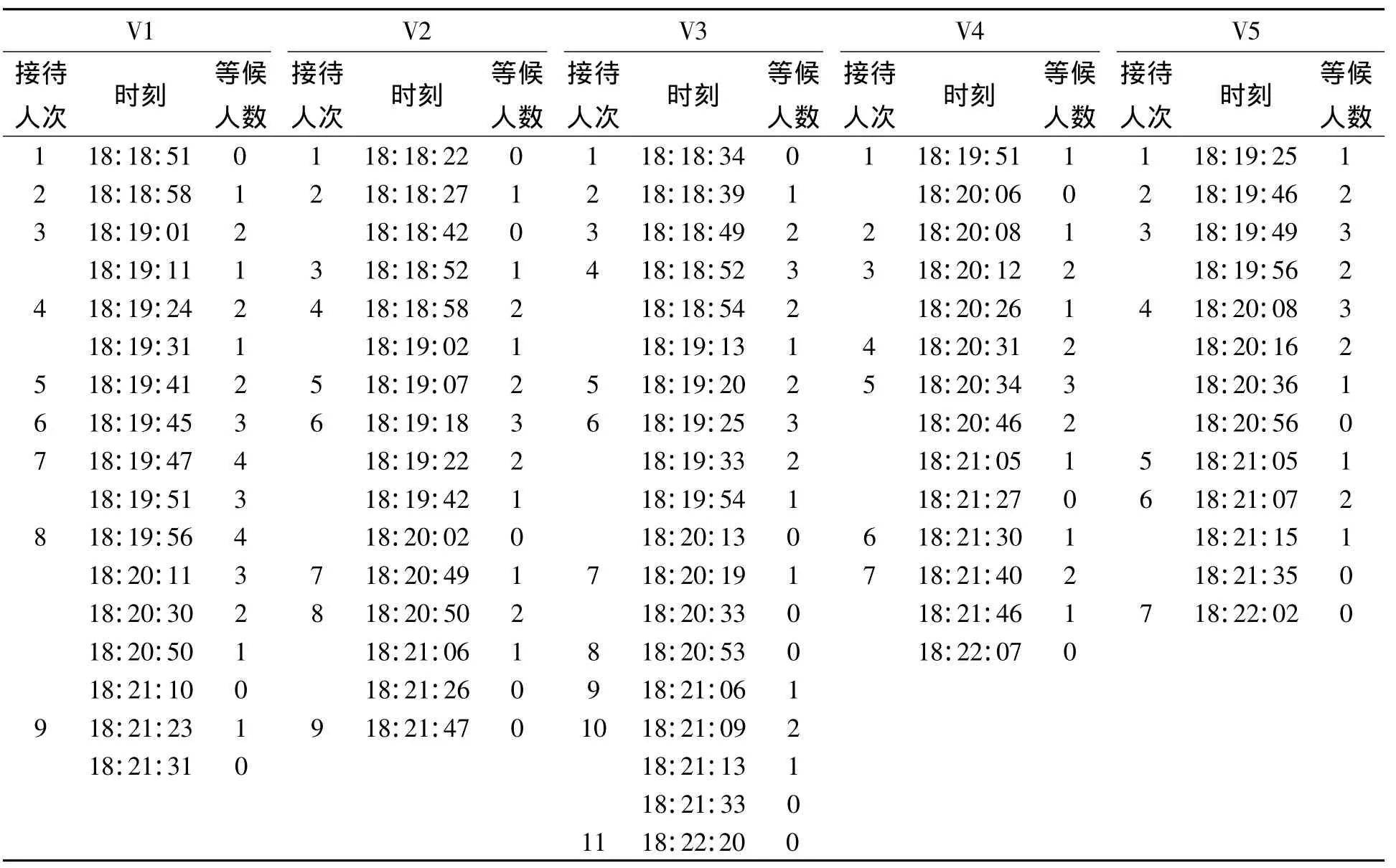
表5 本文模型在“设施利用率”上的结果

3．设施平均等待时间

首先给出设施平均等待时间的定义和计算方法，其为在该设施上的等待时间之和与在该设施上需要等待的游客人数之比值。换句话说，到达设施后由于设施空闲而直接可玩、无须等待的游客并不在指标计算范围之内。设施需要游客排队的平均等待时间间接地反映了景区在各个局部的拥挤程度，可客观反映景区的整体运营情况。如果各个设施的平均等待时间相差无几，则说明人群分布越均匀，拥挤程度越低。

从表6的结果来看，各设施的平均等待时间基本相同，这表明人流分布上具有较高的均匀度，并没有出现在个别设施外高度集中、大量游客排队等候，而其他设施外游客寥寥无几的情况。

表6 本文模型在“设施平均等待时间”上的结果

四、导览效果

为了彰显本文模型的优越性，在这一节中，与其他相关文献的导览系统做一个比较。从表7整理的结果来看，4篇文献构建的系统能同时实现两种效果，其余7篇文献则只能实现一种效果。可见，从景区管理角度来看，本文模型能改善景区客流分布状况，降低人群拥挤的程度;从景点接待能力来看，能优化设施之间的负荷均衡，避免某些时刻游客在个别游乐设施过于拥挤，而其他设施游客寥寥无几的情况;从游客角度来看，能提升游客的游玩效率，减少游客在寻找和等待上的游玩成本。

五、结论与讨论

大型游乐场减少人群拥挤的一个关键措施就是合理地调节游客的参观路线或游览行程，使人流在时间、空间上能均匀分布。为达到这一目的，本文针对游客行进路线问题，设计了一种全新的智能导览系统。与已有文献大多从全路线协调控制的思路出发相比，本文通过单步协调控制来确定游客的下一个参观点。为此，本文首先构建了基于择优选择机制的逐次决策算法，同时考虑停留点的状态、属性和游客本身的需求，由此来获得单步最少代价的路径。然后，通过一个简单算例验证了本文模型在游客等待时间、设施利用率和设施平均等待时间三个指标上的良好性能。从研究结果来看，本文模型能提前告知游客候选项目能否游玩，因此不会出现当游客到达项目后才发现项目来不及游玩(已关闭或者等候人数太多超过其关闭时刻)的情况，也不会导致到达游乐场时刻较早的游客等待时间较短，到达时刻较晚的游客等待时间较长的局面。此外，本文模型能最大限度减少某些设施繁忙，而其他设施闲置的现象发生。总的来看，本文所创建的智能导览系统，能让游客自动散布到各个有剩余容量或不太拥挤的设施上，均衡利用各设施的接待能力，非常适合应用于排队问题突出的大型游乐场的经营管理中。

研究的不足之处在于，本文模型的研究效果还停留在实验室阶段，其实际效用如何，还需要在实践中进一步检验。未来的研究工作还包括模型的进一步优化、与其他模型的更为全面的结果比较以及更合理的样本数据采集。

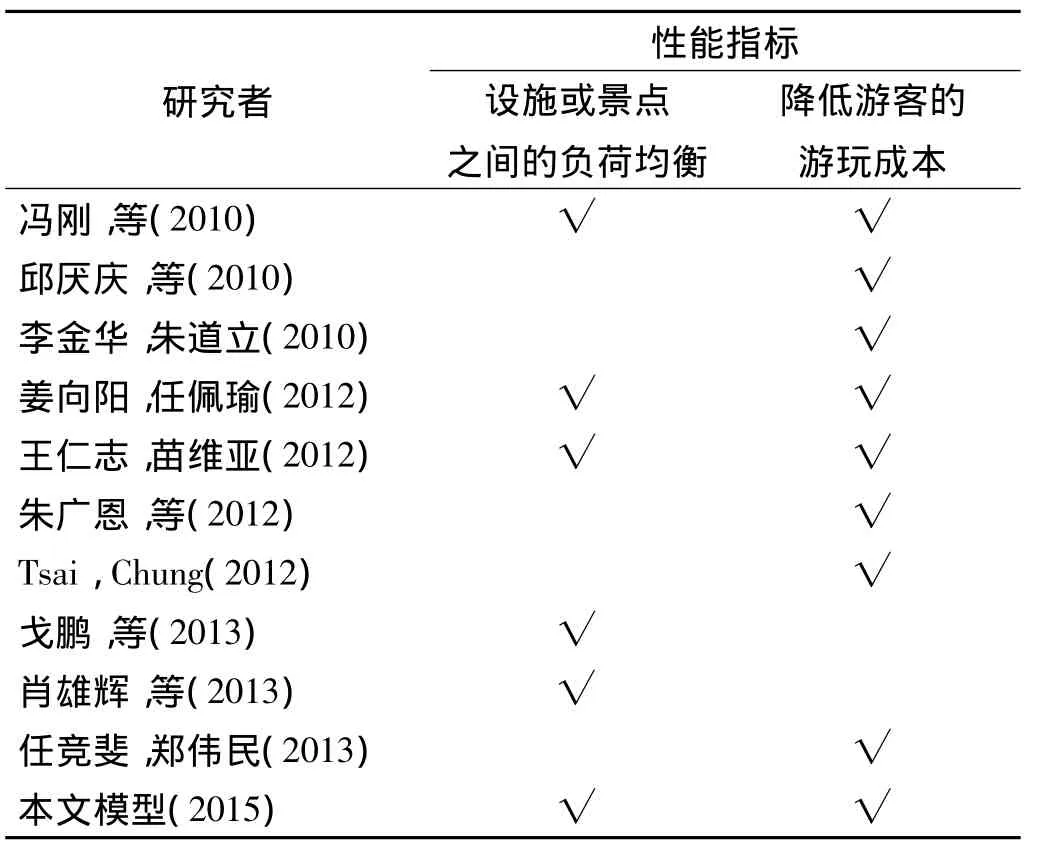
表7 几种景区智能导览系统的效果对比