广义正定矩阵的相关性质及其判定

朱萍萍，李双东，韩 钰

(安徽大学 江淮学院，安徽 合肥 230039)

二次型与对称矩阵一一对应，判断二次型的正定性即判断方阵的正定性，且任意一个二次型所对应的矩阵不仅可以表示成对称矩阵，还可以表示成其他形式的矩阵.例如，二次型

(1)

1 广义正定矩阵的概念及其相关性质

定义1 设A∈Rn×n，如果∀X=(x1,x2,…,xn)T∈Rn，且X≠0都有XTAX>0，则称A为实正定矩阵，记A∈P1，若XTAX≥0，则称A为实半正定矩阵.

定义2 设A∈Rn×n，如果∀X=(x1,x2,…,xn)T∈Rn，且X≠0，都存在实对称正定矩阵S，使得XTSAX>0，则称A为实正定矩阵，记A∈P2，若XTAX≥0，则称A为实半正定矩阵.

以上两种定义的矩阵统称为广义正定矩阵及广义半正定矩阵.若A可逆，则A=ΛQ，Λ为正实对角阵，Q为正交阵，则xTΛQx>0，由定义2知矩阵Q广义正定.

性质1 若矩阵A∈P2，则AT∈P2，A-1∈P2，A*∈P2，KA∈P2(K>0).

证明 (1)A∈P2⟹∀X≠0,X∈Rn×1，有XTSAX>0⟹XTATSX>0.取A=AS-1S，则可得XTST(S-1)TATSX>0，令Y=SX，有YTS-1ATY>0⟹AT∈P2.

(2)A∈P2⟹∀X≠0,X∈Rn×1，有XTSAX>0⟹X-1A-1S-1(XT)-1>0，取A-1=S-1SA-1，则可得X-1S-1SA-1S-1(XT)-1>0 ，令Y=(XTS)-1，有YTSA-1Y>0⟹A-1∈P2.

(3)A*=|A|A-1，由(2)得A*∈P2，显然，KA∈P2.

性质2 若矩阵A,B∈P2,t>0,则A+tB∈P2. 证明A∈P2⟹∀X≠0，X∈Rn×1,存在可逆对称矩阵S1，使得XTS1AX>0.B∈P2⟹∀X≠0,X∈Rn×1，存在可逆对称矩阵S2，使得XTS2tBX>0，显然，XTS1AX+XTS2tBX>0，因此，A+tB∈P2.

性质3 若矩阵A∈P2,则存在对称正定矩阵B，使得BA+ATB对称且正定.

证明A∈P2，∀X≠0,X∈Rn×1，存在可逆对称矩阵B，使得XTBAX>0，

XTATBX=(XTBAX)T>0⟹X≠0，X∈Rn×1，XTBAX+XTATBX>0，又由于(BA+ATB)T=BA+ATB，从而性质得证.

性质4 若矩阵A∈P2，Q为正交阵，则QTAQ∈P2.

证明A∈P2⟹∀X≠0,X∈Rn×1，存在对称正定矩阵S,使得XTSAX>0，又由于QTSQ对称正定，所以XT(QTSQ)(QTAQ)X=(QX)TSA(QX)>0，故QTAQ∈P2.

因此，

2 广义正定矩阵的判定

2.1 矩阵A广义正定的充分必要条件是A对应的二次型正定.

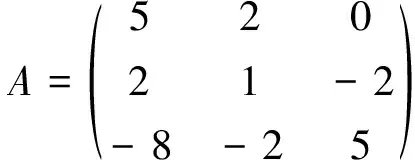
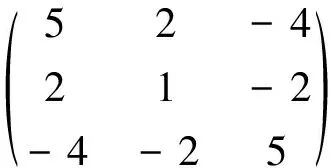
2.2 A广义正定(A∈P1)的充分必要条件是为对称正定矩阵

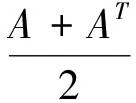
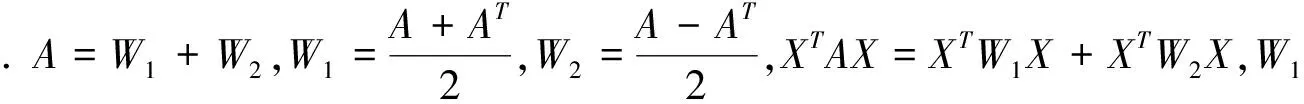
2.3 广义正定的充分必要条件是A=BC或A=CB，B为正定对称矩阵，C为正定矩阵

证明 必要性 (1)A广义正定，A∈P2，则∀X∈Rn×1，且X≠0，存在对称正定矩阵S，使得XTSAX>0，令SA=A1，即XTA1X>0，A1∈P2，A=S-1A1，B=S-1，C=A1，从而得到A=BC.

(2)A∈P2，由性质1得AT∈P2，则∀X∈Rn×1，且X≠0，存在实对称正定矩阵S，使得XTSATX>0，SAT=A1，即

XTA1X>0,A1∈P1,AT=S-1A1⟹
A=A1T(S-1)T,C=A1T,B=(S-1)T⟹A=CB;

充分性 (1)A=BC，C=B-1A，C∈P1，则∀X∈Rn×1，且X≠0，XTCX=XTB-1AX>0，因此，A广义正定.

(2)A=CB，AT=BTCT，CT=P1，CT=(BT)-1AT，则∀X∈Rn×1，且X≠0，XTCX=XTB-1AX>0，A广义正定.

XTCTX=XT(BT)-1ATX>0⟹AT∈P2

由性质1得A广义正定.