基于最小平方法的微震震级与能量关系研究

王元杰，霍永金，张宗文，王传朋，赵成利

(1.天地科技股份有限公司开采设计事业部，北京100013;2.煤炭科学研究总院开采设计研究分院，北京100013;3.中天合创能源有限责任公司，内蒙古鄂尔多斯017000;4.新汶矿业集团有限责任公司华丰煤矿，山东泰安271413)

微震监测技术 (MS)是通过监测煤岩体受力变形和破坏后发射出的震动波来进行监测工程岩体稳定性的技术方法［1］。微震监测技术作为一种区域性、实时性的监测技术，与其他传统的监测手段如钻屑法等相比，具有远距离、三维、实时、动态监测的特点，并且微震监测具有很高的定位精度，已经成为目前监测煤岩体动力灾害的主要技术手段［2］。目前，国内应用的微震监测系统多为引进国外或自发研制，如:新汶华丰煤矿与天地科技股份有限公司合作引进的波兰ARAMIS M/E微震监测系统;冬瓜山煤矿与唐礼忠等合作引进的南非ISS微震监测系统;凡口铅锌矿与李庶林等合作研制的微震监测系统;徐建新和刘英利合作研制的微震监测系统等［3］。

1 微震震级与能量的关系

微震事件对煤岩体稳定性的影响程度大小取决于微震事件能量释放多少，微震监测系统监测得到的只是各传感器接收到的由震动机械能转化成的电压值，再把监测到的电压值转化为能量值，根据此能量值，在考虑地震波在传播过程中因为反射、折射、透射等造成的衰减基础上，得到震源能量和距离之间的能量关系式，从而推算出震源能量值［4－5］。

ARAMIS M/E微震监测系统采用综合能量计算法计算微震事件的能量，能量的计算公式为:

其中，

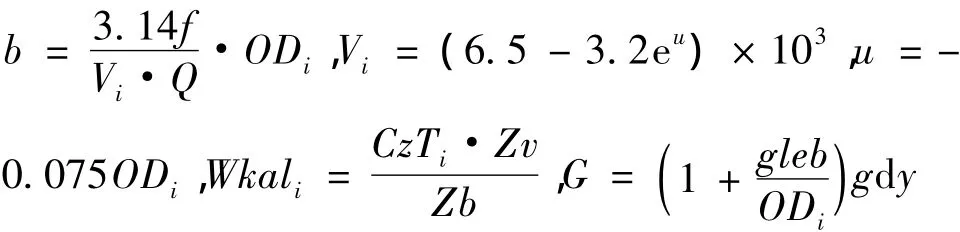
式中，Ei为第i个拾震器计算得到的能量值;ODi为第i个拾震器距震源的距离;Vi为由理论公式得到的波速;f为极限频率;Q为介质阻尼;CzTi为第i个拾震器的线性灵敏度;leb为震源深度 (Z坐标+测量处的标高);Ai，k为第i个拾震器的信号振幅;Npi为第i个拾震器初始信号振幅;Nki为第i个拾震器结束信号振幅;Zv为按速率表示的测量范围;Zb为按bits表示的测量范围;Takt为每秒取样次数;G为介质密度。

该方法解决了对微震事件能量估计的问题，计算结果以焦耳为单位。但是，如果信号过强，某个拾振器信号里达到最大振幅的信号过多，通过这种信号得到的能量值准确性将受影响，用该拾振器计算得到的能量值不用于参与计算能量的均值。

微震震级的计算方法源于地震震级的计算方法，地震震级是通过测量地震波中的某个震相的振幅和周期，并考虑地震波传播过程中的衰减计算得到的一个衡量地震相对大小的量，最早由美国的CharlesF.Riehter和日本的 Kiyoo Wadati在20世纪30年代提出的［6］，根据人对地震的感觉和地震的破坏程度将里氏震级划分9个级别，3级以下的地震属于弱震，人们一般不易觉察;6级以上属于强震，根据震源的不同深度会造成严重的破坏和损坏［7］。地震的能量是根据地震仪记录到的地震波振幅和周期计算得到的，地震的震级由能量推算得出，地震释放出的能量与震级成正比，能量越大，震级越大［8］。震级 (M)和震源能量 (E)的关系为:

式中，a，b为常数，不同煤矿震级－能量关系式的a，b参数是不一样的，因而结合煤矿具体的地质条件、开采状况，很有必要确定不同煤矿的震级－能量关系式参数。

2 最小平方法优化参数

在科学研究中为了找出某些相关量之间的规律，通常采用数据拟合的方法，主要有传统的三角函数逼近法、Pade逼近法、插值法、最佳一致逼近多项式法、最佳平方逼近、最小平方拟合等，以及现代的模糊逼近法、神经网络逼近法、小波理论法、支持向量机函数逼近法等［9］。

最小平方拟合是一种最基本的计算方法，广泛应用于建模中，解决问题时简明而清晰，特别在大数据分析研究中，具有非常重要的作用和地位。最小平方法通过计算最小化误差的平方和来求解数据的最佳函数。

假设直角坐标系中的一组数据 (x1，y1)，(x2，y2)，…，(xi，yi)，采用数学优化技术可以找到这些数据之间的函数关系。如果坐标系中的这些数据图像近似于一条直线，就可以用直线方程:y=a+bx来表达这组数据的函数关系。最小平方法就是找到各种观测数据之间函数关系的一种数学优化基本计算方法，它的原理是当最小误差平方和S=Σ [yi－(a+bxi)]2为最小时，即

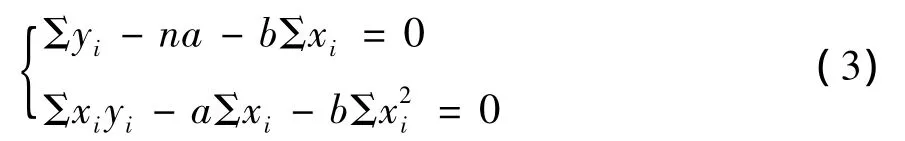
解得系数a，b为

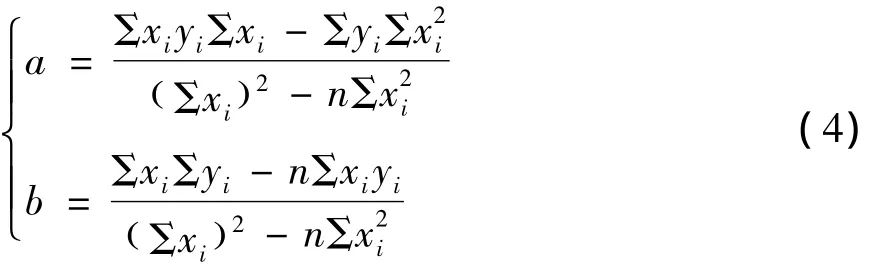
3 应用验证

华丰煤矿于2006年引进并装备了波兰ARAMIS M/E微震监测系统，截至目前已获得了大量的监测数据，作为后续分析的基础，如何保证监测数据的可靠性至关重要［10］。最初ARAMIS M/E微震监测系统计算得到震级对比当地地震台提供的里氏震级误差很大，微震监测系统计算得到的震级普遍高于地震台提供的里氏震级，两者差值最大的达到1.1级。针对微震系统计算得到震级误差较大的问题，需要优化震级－能量关系式参数，使得系统计算得到的震级和当地地震台提供数据更加吻合，提高系统数据的可靠性。华丰煤矿微震监测系统最初震级－能量关系式参数系数a和b，由波兰地球物理学家Marek Dworak结合其在波兰多年工作经验设定，分别为a=2.2，b=1.9。

根据震级和震源发出的总能量之间关系lgE=a+bM，震源发出的总能量E的常用对数与震级M成线性关系，采用多个地震台提供的震级数据作为计算震级－能量对应关系的样本点，通过最小化误差的平方和寻找数据的最佳直线匹配。如表1所示，设地震台震级为xi，对应的微震系统计算能量的常用对数为yi，运用最小平方法生成震级－能量对数对应直线lgE=3.484+2.123M，如图1所示，图中的点代表样本点，直线为震级－能量对数对应直线。

为验证新的直线关系对于系统计算震级的误差，选取多个地震台数据与系统数据，并通过新的震级－能量关系式参数a=3.484，b=2.123计算得到新的震级，如表2所示。结果显示采用最小平方法减小了系统震级的误差，提高了微震监测系统监测数据的可靠性。

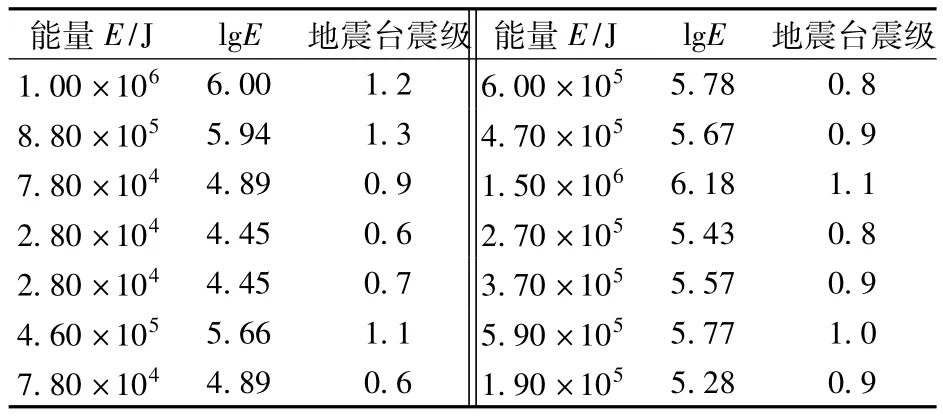
表1 震级调整计算对比结果

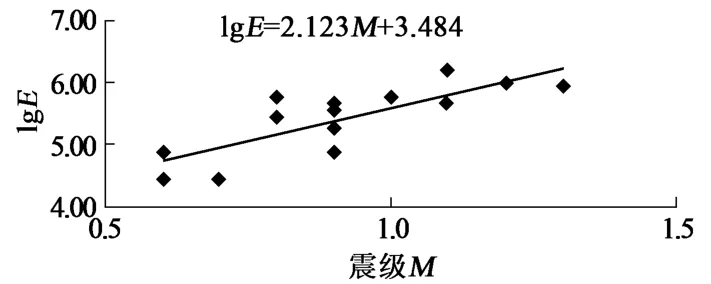
图1 震级－能量对数对应直线

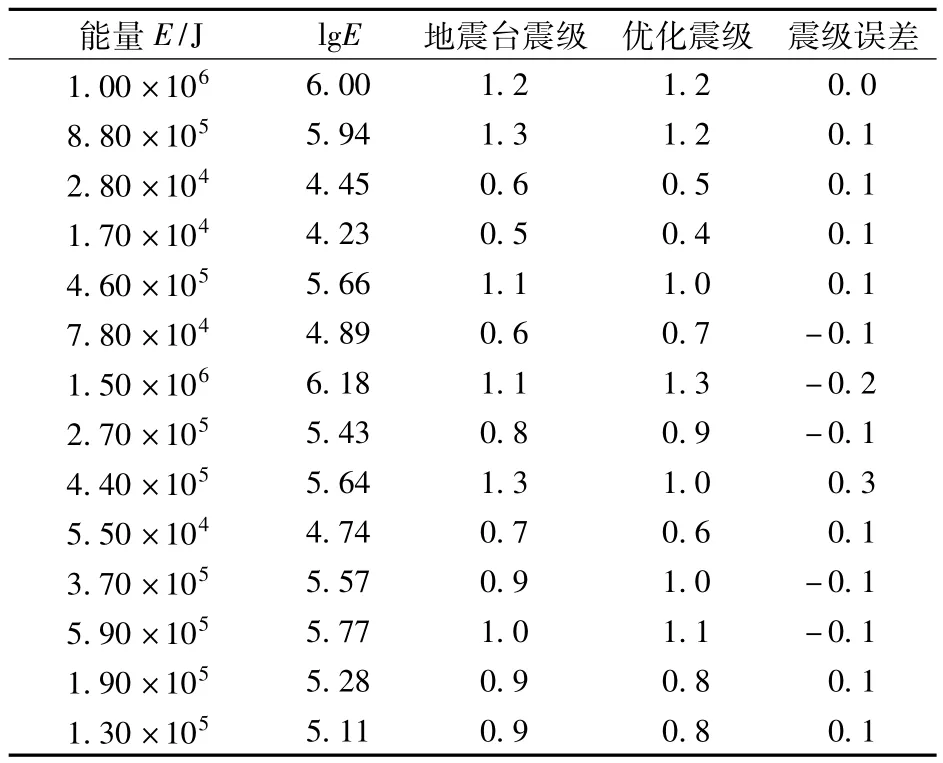
表2 震级调整计算对比结果

4 总结

采用最小平方法得出微震监测系统的震级－能量关系式参数:a=3.484，b=2.123。通过该参数得出的系统震级与当地地震台震级的误差明显地减小。震级－能量关系式参数的优化取得了良好的效果，提高了华丰煤矿微震监测数据的可靠性，并为类似矿井微震监测系统的建设提供了借鉴和指导意义。

［1］齐庆新，窦林名.冲击地压理论与技术［M］.徐州:中国矿业大学出版社，2008.

［2］窦林名，何学秋.冲击地压理论与防治技术［M］.徐州:中国矿业大学出版社，2001.

［3］唐礼忠，潘长良，杨承祥，等.冬瓜山铜矿微震监测系统及其应用研究 ［J］.金属矿山，2006(10):41－44，86.

［4］张宗文，王元杰，赵成利，等.微震和地音综合监测在冲击地压防治中的应用［J］.煤炭科学技术，2011，39(1):44－47.

［5］王元杰，邓志刚，王传朋.提高深部开采微震事件定位精度的研究 ［J］.中国煤炭，2011，37(12):60－63，81.

［6］Aleksander Cianciara，Bogdan Cianciara.Method of predicting tremors on the basis of seismic emission registered in exploitation workings［C］.Tectonophysics，456(2008).

［7］刘英利，徐建新.强震与微震观测系统的研究［J］.地震工程与工程振动，2006，26(3):264－266.

［8］李庶林，尹贤刚，郑文达，等.凡口铅锌矿多通道微震监测系统及其应用研究 ［J］.岩石力学与工程学报，2005，24(12):2048－2053.

［9］鲁振华，张连城.门头沟矿微震的近场监测效能评估［J］.地震，1989(10):32－39.

［10］陈炳瑞，冯夏庭，李庶林.基于粒子群算法的岩体微震源分层定位方法 ［J］.岩石力学与工程学报，2009，28(4):740－749.