单级悬臂式挡墙振动台模型试验与动力分析

傅志明

(中铁二十四局集团新余工程有限公司，江西 新余 338000）

单级悬臂式挡墙振动台模型试验与动力分析

傅志明

(中铁二十四局集团新余工程有限公司，江西 新余 338000）

根据相似关系理论，对小型振动台模型试验的相似关系进行设计，确定模型试验相似常数，确定模型试验的相似材料及其主要物理力学参数。通过振动台模型试验，研究了以砂土为填料在水平地震作用下单级悬臂式挡土墙的动力特性。测试了单级悬臂式挡土墙模型在不同峰值的水平地震作用下的加速度、动位移及侧向动土压力随挡墙高度的变化规律。通过实例分析，为今后单级悬臂式挡土墙的抗震设计提供参考。

单级悬臂式挡土墙；振动台模型试验；水平地震加速度；动力特性

0 引言

地震边坡破坏导致严重性灾害而广泛引起人们的关注，当发生强烈地震时，地震会诱发挡土墙破坏，尤其山岳地区，比地震直接造成的危害大很多。因此，对边坡的稳定性在地震作用下进行正确评价和进行综合治理就变得非常重要了。近年来，专家和学者高度重视岩土边坡地震崩滑问题，并对此进行深入的研究同时取得了可喜的成果。在铁路及公路路基工程中，挡土墙主要被用来承受土体的侧向土压力，同时在稳定路堤、隧道洞口、路堑以及桥梁两端的路基边坡等各类工程中也得到了广泛的应用。在水利、矿场及房屋建筑工程中，挡土墙主要是维持加固山坡、基坑边坡和河流岸壁等的稳定性。

当上述工程或其他岩土工程遇到了不良的地质灾害时，挡土墙的主要作用使加固或拦挡不良地质体，如加固滑坡、崩塌及岩堆体，泥石流和拦挡落石等[2]。挡土墙、桥台等挡土建筑物遭到破坏也是非常常见的[3]，然而由于地震的强度不一，挡土墙发生的破坏模式也不尽相同，部分挡土墙因发生较大的位移，从而失去了其应有的防护功能或影响了附近其它的建筑物[4]，导致被保护的坡体坍塌或建筑物发生失稳破坏；部分挡土墙因本身强度不够而发生剪断；此外，有的挡土墙也会发生局部破坏。但值得注意的是，虽然有一部分挡土墙发生了位移甚至破坏，而另一部分却完好无损[5]。

杨剑[6]应用拟动力法来考虑在动力荷载下的周期、纵波及横波效应，并分析了挡土墙后的由地震产生的被动土压力进行分析。陈学良等[7]首先对挡土墙抗震研究中的三个重要问题即弱粘性土地震土压力、水平地震作用沿墙高分布、挡墙体系考虑水的作用进行了概述。Shodolapo Oluyemi Franklin[8]等对传统的CECP2方法及其更改后的极限状态设计方法BS8002，运用于悬臂式挡土墙的结果进行了研究和对比，结果证明：在所有情况下实现了滑动和倾覆稳定性。RobertW.Day[9]通过研究两个挡土墙破坏的案例，来论述钢筋悬臂式挡土墙的设计和施工。对第一种情况，墙体的破坏是由于减少了横向支撑；而第二种情况，墙体的破坏是由北岭地震造成的侧向压力的增加。Koichi Akai[10]等对Tanata、Amagasaki和Tsukamoto 三个地区的土工格栅加筋土挡土墙，在不同地震烈度条件下的破坏情况进行对比分析。

从国内外对悬臂式挡土墙的研究表明，国内外对悬臂式挡土墙的地震动力特性的试验研究相对较少，对多级挡土墙等的地震动力特性的研究则更少。悬臂式挡土墙是目前应用比较广泛的轻型支挡结构之一，其具有结构轻型、占面积少、预制制拼接、便于施工等工程特点。而以往研究的悬臂式挡土墙主要是单级的[11.12]，基于此，进一步对悬臂式挡土墙的抗震性能分析就显得非常迫切了，不仅对悬臂式挡墙在地震频繁发生地带中的建设提供了科学的理论依据及指导意义，还将对悬臂式挡墙的抗震性能设计标准化建设有非常重要的参考价值。本文拟通过室内模型试验对单级垛式悬臂式挡墙在地震作用下的抗震性能进行分析，以期为今后类似工程在地震作用下的建设提供一些有益的施工建议。

1 单级垛式悬臂式挡土墙抗震模型试验设计

本次模型试验在兰州交通大学土木工程学院实验室完成，主要目的在于研究：单级垛式悬臂式挡土墙在地震作用下的动力响应特性。本文进行悬臂式挡土墙振动模型试验的主要目标是将原型单级垛式悬臂式挡土墙在动力荷载作用下的力学现象，在单级模型悬臂式挡墙上进行相似模拟，测量单级模型悬臂式挡墙中的动应力、动位移、水平加速度响应等物理量，再通过一定的相似关系反算到原型单级垛式悬臂式挡土墙上，这种相似关系被称为模型的相似律。本模型试验采用1：40比例尺的缩尺试验，模型箱的净尺寸为30cm×7cm×12cm(长×宽×高)。设计标准之一就是最小化有效荷载，以便振动台系统可以提供较大的水平地基输入运动。为了减少重量，模型箱采用0.5 cm厚木板制作，模型箱重1.3kg，模型箱与振动台采用螺栓连接，如图1所示。

图1 模型箱与振动台固定

试验过程所用的回填土为中细砂，图1.2给出了砂土粒径级配累积曲线。根据室内土工试验结果，测得砂土的最大干密度为1.73g/cm3，填筑模型时，砂土填料的压实度均按0.75控制。

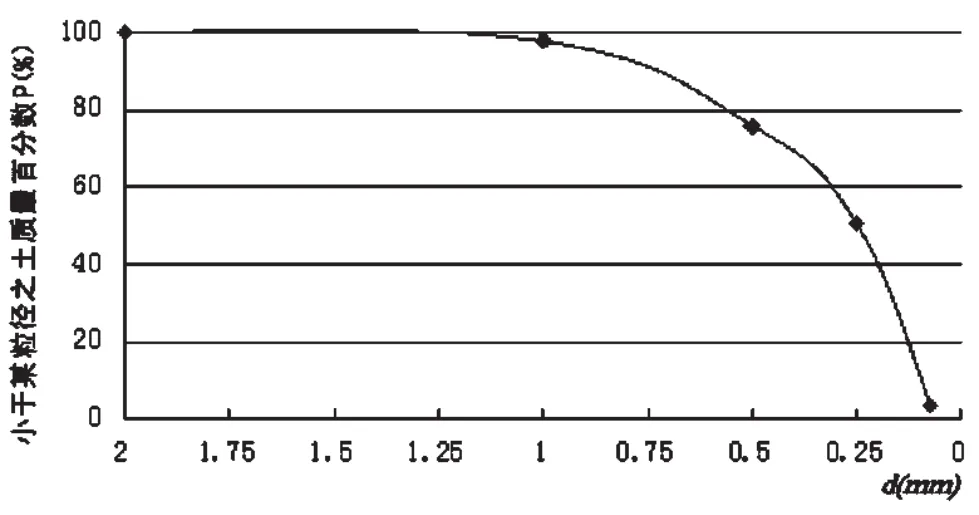
图2 砂土粒径级配累积曲线

砂土分层回填的高度与水平排列的仪表对应，每层回填整平后，加速度计和机电百分表也分别固定在特定的位置。整个模型完成过程如图3-4。挡墙用有机玻璃制作而成，参考文献资料，确定有机玻璃的杨氏模量E和泊松比υ分别是3.5×104MPa和0.25。挡墙都是由底板和立臂组成倒T字型截面。根据几何相似关系，本文研究的单级垛式悬臂式挡土墙立臂高度为10cm。

图3 各种仪表布置位置

图4 模型-仪表-设备系统

同时由于模型尺寸限制，并考虑应变测试线对模型振动试验的影响，动加速度计共布置了3个，编号为①～③，其中①点对应上墙10cm处;②点对应上墙5cm处;③点对于上墙0cm处。动位移计和应变计各布置了3个编号为A～C，各仪表具体位置布置如图5所示。

图5 各种传感器布置图

地震波采用振动台自带的汶川地震波[13]，该地震波经过调整和校核，其峰值加速度为1.0m/s2，汶川地震波如图6所示，并可根据不同水平地震加速度调整为本文所研究的不同水平地震加速度峰值即：0.2g、0.3g、0.4g。

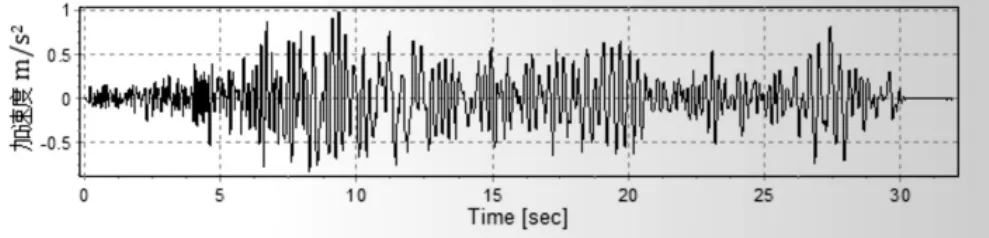
图6 汶川地震波时程曲线

2 试验结果及动力分析

2.1 立臂水平加速度响应

图2.1为单级垛式悬臂式挡墙在水平地震最大加速度为0.2g、0.3g、0.4g条件下，立臂不同位置处的加速度时程曲线。

表2.1为砂土填土材料，在水平地震加速度峰值分别为0.2g、0.3g、0.4g时，单级垛式悬臂式挡墙上各个测点的加速度峰值。

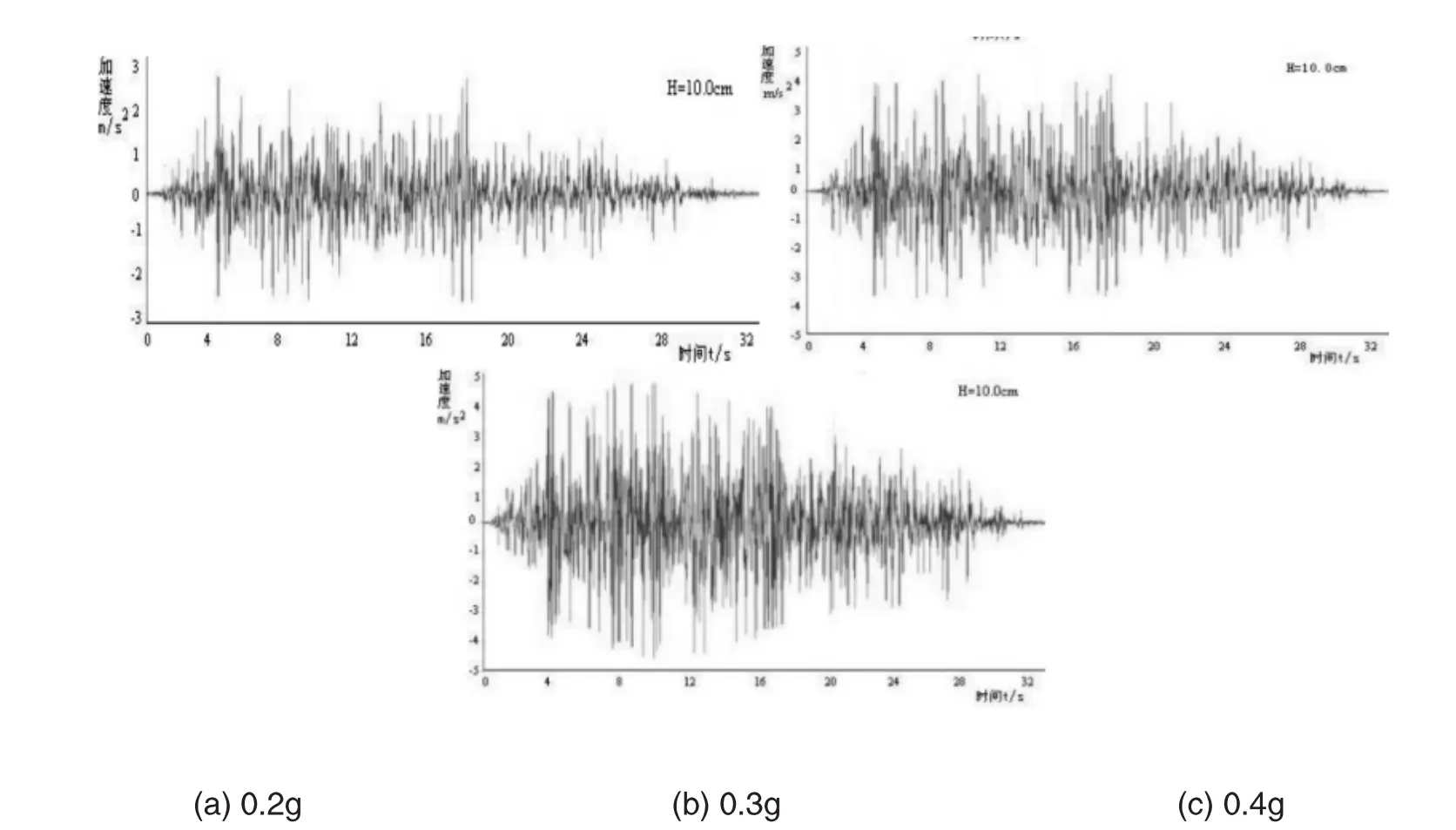
图7 加速度峰值为0.2g、0.3g、0.4g时挡墙的加速度时程曲线

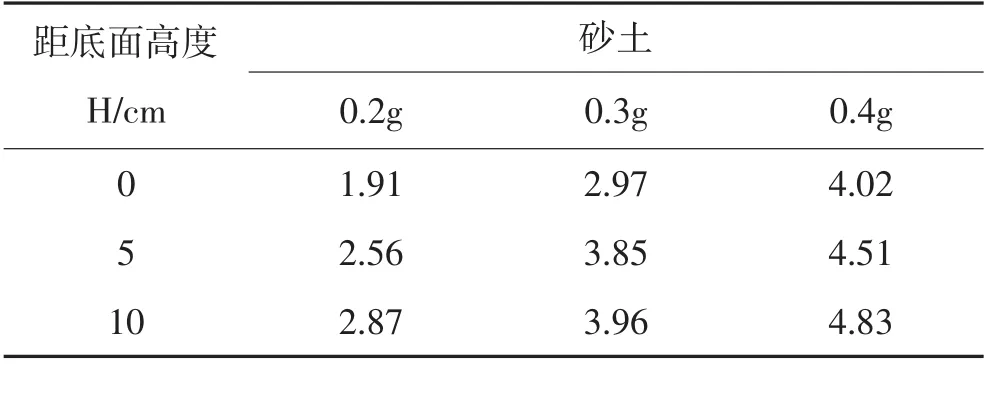
表1 单级垛式悬臂式挡墙加速度峰值(m/s2)

图8 单级垛式悬臂式挡墙加速度峰值分布

由图7～8及表1可见：在不同水平地震加速度下，加速度时程曲线变化形状变化规律相似，即单级垛式悬臂式挡墙随着距底面高度的增加，加速度峰值都呈现逐渐递增趋势。当加速度峰值从0.2g增加到0.4g时，砂土回填的挡墙墙顶的加速度响应值分别增加了50.4%。

2.2 动位移

图9为不同水平地震加速度峰值条件下，单级垛式悬臂式挡土墙墙背动位移随墙高的分布。

不同水平地震加速度峰值下，动位移s/H（水平动位移s与墙高H的比值）随墙高的变化如图9所示，由图可得：

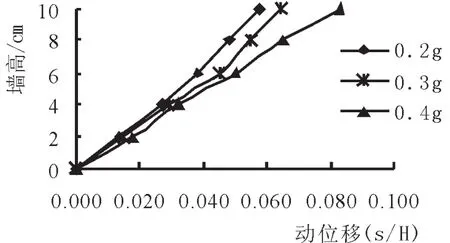
图9 挡墙动位移s/H随墙高的变化

1.在不同水平地震加速度峰值作用下，单级垛式悬臂式挡墙随着墙高的增高而逐渐增大，且最大值出现在墙顶处。

2.当加速度峰值为0.2g，上墙墙顶的动位移s/H最大，达到0.065，且远离回填方向移动，而其墙底的动位移则较小，则基本上反映出上墙动位移是线性变化的。从挡墙上墙的总体位移变化情况可以明显观察到，上墙是绕墙底某点发生了转动并同时也伴随着挡墙下沉。从而反映出挡墙基底的承载能力对挡墙动位移的影响较大。当峰值增加到0.4g时，其动位移s/H最大值达到0.099，约是0.2g的1.5倍。

综上可见，单级垛式悬臂式挡墙的总体位移趋势基本上是远离填土方向移动的。

2.3 动应力

图10为不同水平地震加速度峰值条件下，单级垛式悬臂式挡土墙墙背动应力随墙高的分布。

表2为砂土填土材料，在水平地震加速度峰值分别为0.2g、0.3g、0.4g下，单级垛式悬臂式挡墙墙后侧向动应力的最大值。

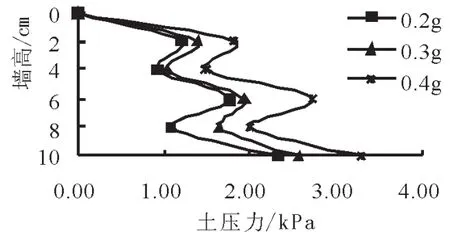
图10 墙背动应力分布

表2 挡墙动应力的最大值(kPa)

1.在不同水平地震作用下的墙后侧向动土压力分布曲线类似，随着墙高的增加逐渐的增大，近似为三角形分布，且最大动土压力都出现在墙底，但与荷载作用下的静土压力呈线性分布有所不同的是，其所测的动土压力分布呈非线性分布；

2.在相同水平地震作用下，地震加速度峰值为0.2g时，砂土的墙后土压力为2.34kPa，但随着峰值加速度的增大，土压力非线性分布、数值也发生巨大变化。整体来看地震加速度为0.4g时，砂土的最大土压力增加到3.31kPa，增加了41%。这说明在相同地震加速度作用下，由于砂土为无粘性土，墙后填土中出现了裂缝，并逐步形成了贯通的破裂面。

3 结语

3.1 单级悬臂式挡土墙水平地震加速度随着墙高的增加而呈递增趋势，且加速度峰值都发生在挡墙墙顶。

3.2 在不同水平地震加速度峰值作用下，单级悬臂式挡墙的水平动位移随着墙高的增高而逐渐增大。从振动台模型试验的分析得到，单级悬臂式挡土墙整体位移都较小，且挡墙都是远离填土方向移动。

3.3 地震荷载作用下，单级悬臂式挡土墙的动应力分布类似三角形分布。则在设计单级垛式悬臂式挡土墙的时候，挡墙必须满足局部和整体的各个方面的稳定性要求。

3.4 从室内模型试验结果可知：在相同水平地震加速度峰值条件下，挡墙的水平动位移和动应力还要受到挡墙刚度、墙背粗糙程度、填土弹模等因素的影响，当填料一定的情况下，与挡墙高度最为密切。柔性挡墙在弹性变形范围内可以起到一定的卸荷作用，但介于本模型试验中单级悬臂式挡土墙尺寸过小，挡墙刚度较大，而应力又较小，因此其柔性特点没有得到明显的体现。

[1]张国祥.三维边坡滑动面及稳定性的非线性弹塑性有限元分析[D].长沙铁道学院博士学位论文,1999.

[2]李海光等编著.新型支挡结构设计与工程实例(第二版)[M].北京：人民交通出版社，2010.

[3]姚敦呈.挡土墙的地震破坏分析[J].武汉大学学报(工学版)，2003,36(02)：82-87.

[4]何义宏.紫坪铺水库左岸重载公路挡土墙震害调查分析[J].路基工程,2009(144)：192-193.

[5]骆巍.直立式挡土墙地震破坏机理及抗震措施研究[D].大连理工大学硕士学位论文,2012.

[6]杨剑.挡土墙地震被动土压力的拟动力分析[J].防灾减灾工程学报,2012,32(3)：365-371.

[7]陈学良,郑云雷,陈宪麦等.三个抗震问题简析及新型挡土墙地震反应评述[J].世界地震工程.2007,23(2)：118-124.

[8]Shodolapo Oluyemi Franklin,Abiodun Luqman Olopade.A Note On the Analysis and Design of Cantilever Retaining Walls Using the Cecp2 and Bs8002 Methods [J].www.arpapress.com//Volumes/Vol.11,2012,11(1)：117-121.

[9]Robert W.Day.Design and Construction of Cantilevered Retaining Walls [J].Periodical on Structural Design and Construction.ASCE,1997,2(1)：16-21.

[10]Koichi Akai.Geotechnical Reconnaissance of the Effects of the January 17,1995,Hyogoken-NanbuEarthquake,Japan[J].Earthquake Engineering Research Center,University of California at Berkeley,1995.

[11]胡俊强.悬臂式挡土墙低应变动力特性分析[D].重庆：重庆大学,2009.

[12]侯卫红,侯永峰.悬臂式挡土墙受力分析[J].北方交通大学学报,2004,28(4)：16-19.

[13]蔡白洁.加筋土支挡结构的地震反应分析[D].兰州交通大学硕士学位论文,2013.

（责任编辑：陈 辉）

Experiment of Cantilevered Retaining Wall Shaking Table Model and Its Dynamic Analysis

FU Zhi-ming

（China Railway 24th Bureau Group Xinyu Engineering Co.,Ltd.,Xinyu 338000,China）

According to similarity theory,the similarity relations of themain physical quantities were studied in this paper，themain similarity coefficients and the simulation materials and itsmain properties of physical and mechanics for small-scale shaking tablemodel testswere determined.Shaking table testswere conducted on cantilevered retaining wall filled with sand under horizontal seismic loading to investigate the dynamic response of the wall.The horizontal acceleration,dynamic horizontal displacement,dynamic stress of cantilevered retaining wall was achieved by model tests under different peaks of horizontal earthquake incentives.Through case studies,this paper provides reference for the seismic design of cantilevered retaining wall.

cantilevered retaining wall;shaking table model test;horizontal earthquake incentives;dynamic characteristics

G741

A

123（2015）03-0030-05

2014-11-21

傅志明（1988-），男，江西新余人，中铁二十四局集团新余工程有限公司，助理工程师。研究方向：城市轨道设计。