基于动力有限元及遗传算法的地震作用路堑边坡安全系数计算

余庆锋，吴 立，利奕年，刘文刚，王先登（.中国地质大学（武汉）工程学院，湖北　武汉007；.湖北省交通规划设计院，湖北　武汉005；.江苏省交通规划设计院股份有限公司，江苏　南京00；.武汉市政工程设计研究院有限责任公司，湖北 武汉00）

基于动力有限元及遗传算法的地震作用路堑边坡安全系数计算

余庆锋1，2，吴 立1，利奕年2，刘文刚3，王先登4
（1.中国地质大学（武汉）工程学院，湖北武汉430074；2.湖北省交通规划设计院，湖北武汉430051；3.江苏省交通规划设计院股份有限公司，江苏南京210014；4.武汉市政工程设计研究院有限责任公司，湖北 武汉430023）

为研究地震动荷载作用下路堑边坡稳定性及滑动特征，首先对上杭蛟洋至城关高速公路路堑边坡风化玄武岩残坡积土体的物理力学性质开展室内试验研究，得到研究区典型路堑边坡土体含水率、液塑限、剪切强度等物理力学指标；然后将试验所得物理力学参数代入ABAQUS有限元程序对路堑边坡地震响应进行计算，程序输出的位移场用来分析坡顶位移变化，输出的加速度用来计算加速度分布系数；再将动力有限元输出的应力场代入MATLAB编写的遗传算法程序，计算边坡安全系数时程曲线，并智能搜索边坡临界滑动面，得到边坡安全系数随着地震波加速度的变化规律以及滑动面包络线的安全系数范围。

路堑边坡；地震动荷载；安全系数；动力有限元；遗传算法

我国西南部地区在地质构造上属于板块十分活跃地区，受欧亚板块和印度洋板块挤压影响，造成该地区高应力持续累积并不断发生地震。随着我国交通建设的迅速发展，这些地区地震作用下的路堑边坡稳定性研究一直是岩土工程界的一个难点。

目前，国内外对地震作用下边坡的稳定性研究主要基于拟静力法和有限元时程计算法。如闫中华［1］最早基于拟静力法并结合数值规划法对均质及非均质土坝安全系数规律进行求解；孙君实［2］在条分法的基础上，提出用复形法对边坡任意形状滑裂面进行搜索，并求解相应的安全系数；Nguyen［3］则采用单形法搜索边坡任意滑裂面，以求得相应的最小安全系数；陈祖煜［4］开发出STAB程序算法对边坡滑裂面展开搜索，并成功运用于许多工程实例。此外，诸多学者提出遗传算法、人工神经元网络、蚁群算法、进化算法等对地震作用下的边坡稳定性进行分析计算［5-7］，均取得了较好的效果。

但是，对于拟静力法，其原理是以一个参数的形式把地震荷载效应转换为拟静力加速度，由于地震荷载效应具有时程特征，因此该方法无法反映不同时刻边坡所受到的地震作用；对于有限元时程计算法，其优点是能够反映各个时刻的地震作用结果，但该方法仅将坡顶的位移作为边坡失稳的判据，而无法就坡顶位移限值用统一标准来评价，使得其结果的实际应用存在一定偏差。鉴于此，为克服运用拟静力法和有限元时程计算法分析地震荷载作用下边坡稳定性的不足，本文在对上杭蛟洋至城关高速公路路堑边坡土体的物理力学性质开展室内试验研究的基础上，基于动力有限元并结合遗传算法对地震荷载作用下路堑边坡安全系数进行分析计算，一方面通过动力有限元结果来计算边坡安全系数，以体现地震荷载时程特征效应，另一方面应用遗传算法搜索路堑边坡临界滑动面，以体现坡体失稳的直观统一判断标准。

1　路堑边坡土体物理力学性质试验

1.1路堑边坡概况

上杭蛟洋至城关高速公路位于福建省上杭县境内，线路起于蛟洋下道湖村，新建下道湖枢纽互通衔接龙长高速公路，通过设置上杭枢纽半互通实现与国道主干线（永武高速公路）的交通转换。

上杭蛟洋至城关高速公路位于武夷山脉与玳瑁山脉之间的相对低洼地带，地形走向大致呈北北东-南南西向展布，公路沿线主要为侵蚀剥蚀中低山地貌，海拔高程为500～1 778 m。区内地貌地势起伏较大，间夹高差及范围不等的山间盆地，水系呈树状发育，山高谷深，山坡陡峻，为中等切割构造侵蚀山地。

本文选取上杭蛟洋至城关高速公路工程场区具有代表性的路堑边坡（现场路堑边坡见图1，边坡地质剖面示意图见图2），基于动力有限元及遗传算法，对地震荷载作用下的路堑边坡安全系数进行分析计算。

图1　典型玄武岩残坡积土路堑边坡Eig.1 Typical cutting slope of basalt residual soil

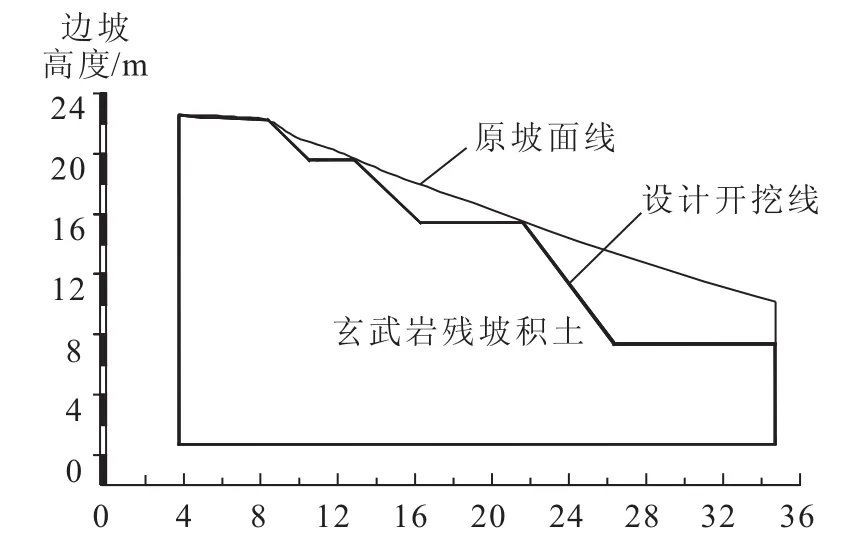
图2　边坡地质剖面示意图Eig.2 Sketch map of slope geological profile

所选边坡属于侵蚀剥蚀中低山地貌，植被茂密，坡面起伏，坡度较陡，达30°～60°，坡体为第四纪覆盖层，风化壳厚达20余米，坡体稳定性差。由于工程场地高程起伏大，大填大挖不断发生，导致在建设过程中出现大量路堑土质边坡。区域内边坡土体多为玄武岩风化残积层，玄武岩风化残积土的工程性质十分特殊，在地震荷载作用下易发生坍塌震陷等工程灾害，导致边坡失稳，因此线路建设必须按高要求抗震设防。根据《建筑抗震设计规范》（GB 50011—2001）［8］，上杭蛟洋至城关高速公路工程场区抗震设防烈度设为8度，基本地震加速度为0.20 g。

1.2路堑边坡玄武岩残坡积土的物理力学性质试验

根据目前勘察资料显示，区域内玄武岩残坡积土地层是玄武岩（M12）在湿热气候长期影响下的风化产物，其厚度从数米到数十米不等，最厚达到40 m。其工程地质特性特殊，孔隙比大，含水量高，易于崩解，在地震荷载累积作用下，一方面容易因为岩土体塑性破坏和孔隙水压力持续上升而发生坍塌滑坡，另一方面区域内风化岩体的结构面特征明显，易受到地震荷载作用后诱发坡体软弱层发生触变软化而导致边坡失稳破坏。鉴于此，有必要先对所研究路堑边坡玄武岩残坡积土的物理力学性质开展室内试验研究，并将试验所得物理力学参数应用于动力有限元分析。

1.2.1常规室内土工试验

首先对现场路堑边坡采集玄武岩残坡积土样，为方便对比，土样分为两组开展常规室内土工平行试验，并通过烘干法测定土样的含水率，锥式液限仪测定土样的液塑限，环刀法测定土样的重度，比重瓶法获取土样的相对密度，其试验结果见表1。

表1　玄武岩残坡积土常规室内土工试验结果Table 1 Conventional laboratory soil test results of basalt residual soil

由表1可见，玄武岩残坡积土的含水率有较大范围的波动，这对坡体稳定性判定产生不利影响；两组土样的液塑限较高，但其液性指数较小。

1.2.2三轴压缩试验

三轴压缩试验采用英国生产的应变控制式三轴压缩仪（INSTRON-1346），该压缩仪由加压系统、压力室和量测系统3个部分组成，见图3。

图3　应变控制式三轴压缩仪Eig.3 Strain control triaxial compression apparatus

三轴压缩试验土样采用现场边坡原状土，将采集的原状土去掉密封皮后削成直径60±5 mm试样，制作好后的土样试件见图4。

三轴压缩试验采用四级围压加载，分别为50 k Pa、100 k Pa、200 k Pa、400 k Pa，终止试验判定条件为:轴向应力量测有峰值时，继续试验直到轴向应变超出5%；轴向应力量测无峰值时，继续试验直到轴向应变超出15%。

试样在天然含水率下进行三轴固结不排水压缩试验，试验后的土样见图5，试验结果见图6。

图4　制作好的土样试件Eig.4 Soil sample for test

图5　试验后的土样Eig.5 Soil sample after test

由图5可见，原状土体在达到峰值剪切强度后，沿着断裂面开始破坏，表明该土体具有明显峰值强度，能够为接下来边坡稳定性计算提供依据。由图6可知，原状土样的应力-应变曲线符合应变软化规律，当轴向应力达到峰值后，土样轴向应变继续增长，此时土样轴向应力逐渐降低，该现象在围压400 k Pa时最为明显，而围压低于400 k Pa时，轴向应力达到峰值后土样轴向应变并没降低，而是缓慢增加或者保持稳定。

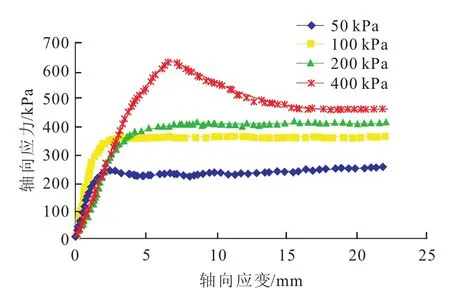
图6　原状土样的应力-应变曲线Eig.6 Test results curves

2　动力有限元分析

本文首先采用ABAQUS有限元程序对路堑边坡地震响应进行计算，将程序输出的位移场用来分析坡顶位移变化，将得到的加速度用来计算加速度分布系数；然后将输出的应力场代入遗传算法程序，计算边坡安全系数时程曲线，并智能搜索边坡临界滑动面。

2.1建模过程

边坡体计算模型采用4节点平面应变CPE4单元，采用单节点弹簧单元SPRING1模拟人工边界，选用DASHPOT1单元模拟人工边界中的阻尼构件，经过对比分析，本文选用刘晶波等［9-11］提出的高精度、参数稳定的一致黏弹性人工边界。模型材料采用Mohr-Coulomb屈服准则和非关联流动势函数。

2.2加载过程

动力加载计算设置两个荷载步，分别为自重荷载步、地震荷载步。首先进行自重荷载步施加:将坡体施加左右边界水平约束，对全部单元施加重力荷载，输出自重荷载作用下的位移场、应力场以及左右约束边界的节点反力；随后进行地震荷载步施加:添加人工边界，取消之前在自重荷载步中设置的水平约束，且将第一步输出的左右约束边界节点反力施加给左右边界节点，以保持平衡，模型基底输入地震波加速度，输出位移场、加速度、应力场。

2.3动力有限元时程计算结果

2.3.1输出位移场

对计算模型基底输入EL-Centro地震波，输入地震波的加速度为0.2 g，设置计算时间为40 s，计算得到路堑边坡坡顶相对位移（坡顶位移减去基底位移）见图7。选取t=15 s时的边坡位移场输出，见图8。

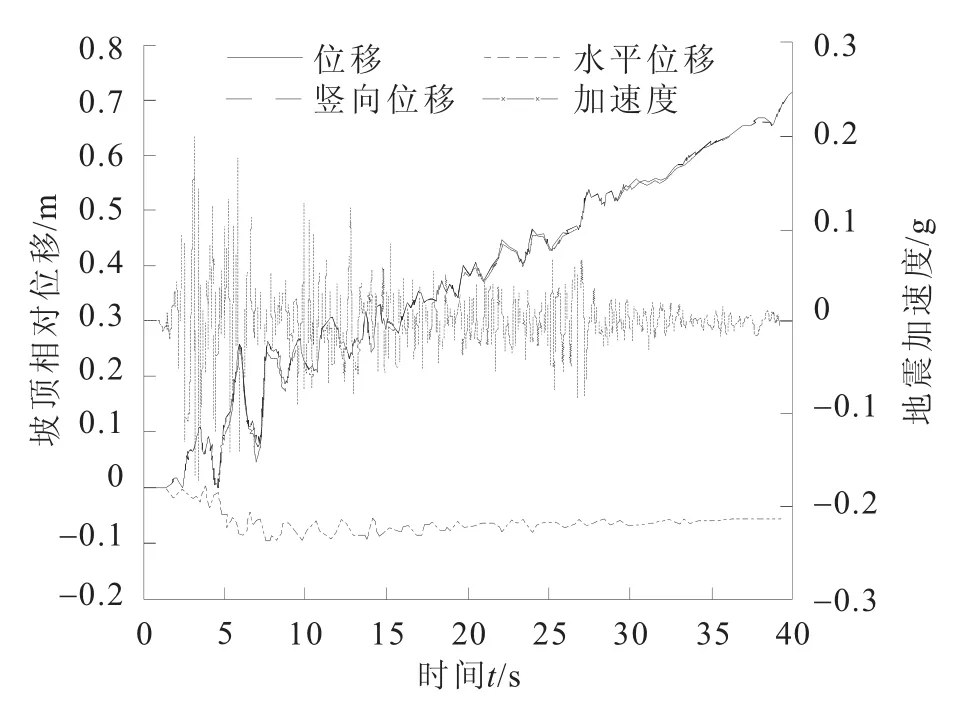
图7　路堑边坡的坡顶相对位移Eig.7 Relative displacement of the dynamic calculation of the cutting slope

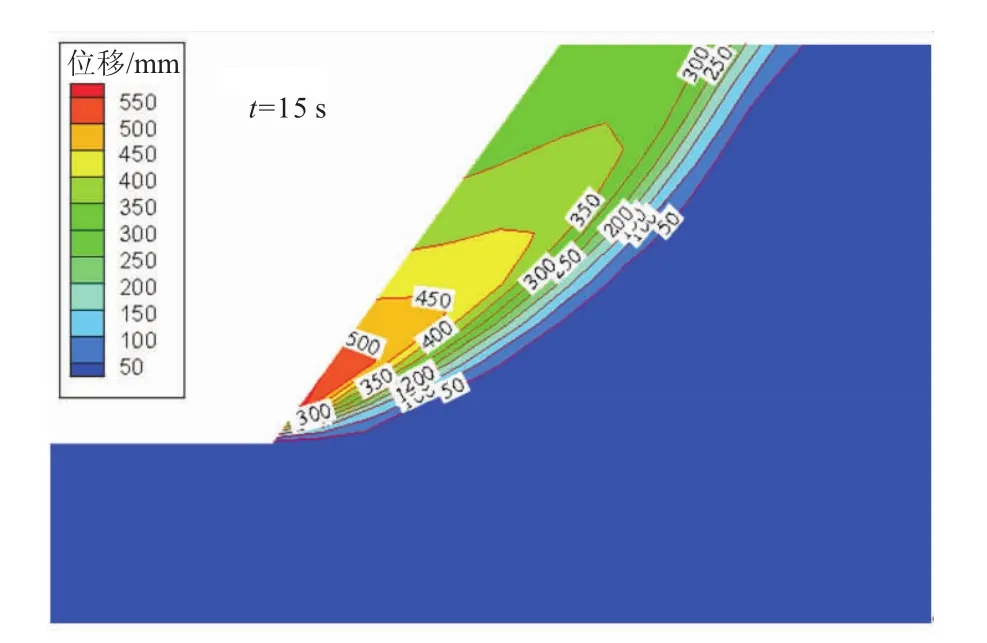
图8　t=15 s时边坡的位移场Eig.8 Displacement field of the cutting slope output at 15 s

由图7可见，输入地震波加速度后，坡顶相对位移不断波动，在40 s时间内整体呈增长趋势，且其波动趋势与地震加速度较为吻合，尤其是地震加速度突变时，坡顶相对位移也随即发生突变；坡体竖向位移较小，其值远小于水平位移，这可用输入的地震波为水平加速度来解释；在t=30 s后，坡顶相对位移上下波动幅度减弱，但增长很快，表明坡体塑性变形持续累积将要达到临界点而发生失稳破坏。

由图8可见，边坡最大位移量为550 mm，最大位移出现在坡脚处，位移量大小由坡脚向坡顶逐步减小，坡顶的最大位移为350 mm；边坡面附近的位移大于边坡的其他部位，且位移随着远离坡面而逐渐减小，在临界滑动面附近，位移降低至50 mm，且由坡脚迅速向坡顶扩展，形成贯通的潜在弧形滑动面。进一步说，如果在震动系数加大、地下水位线上升、降雨量增大的情况下，边坡的变形位移值还将高于此数值计算值，并引发边坡稳定性系数逐步下降，甚至引发边坡失稳。

2.3.2输出应力场

同理，选取t=15 s时的边坡应力场输出，见图9、图10和图11。

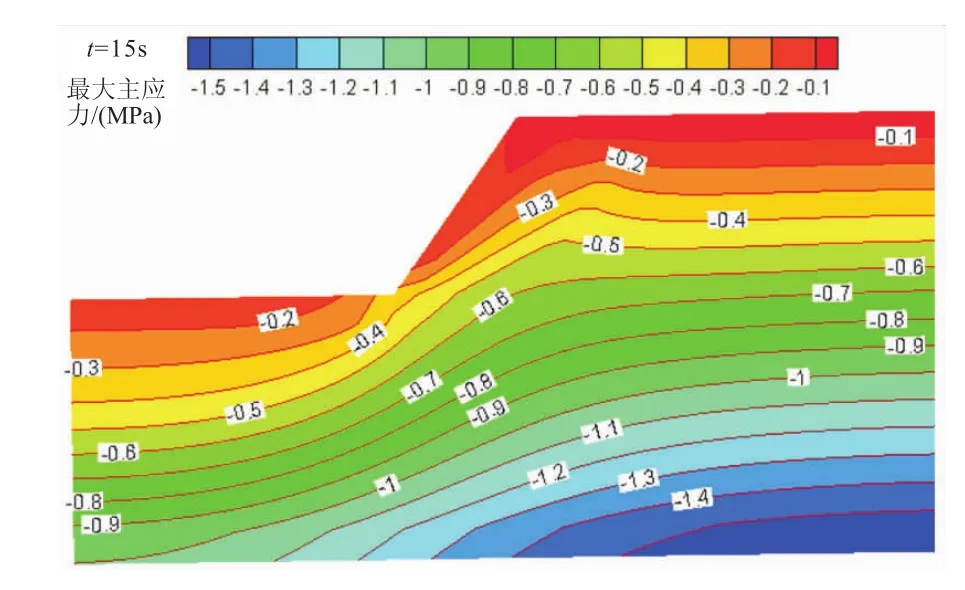
图9　t=15 s时边坡的应力场（最大主应力）Eig.9 Maximum principal stress field of the cutting slope output at 15 s

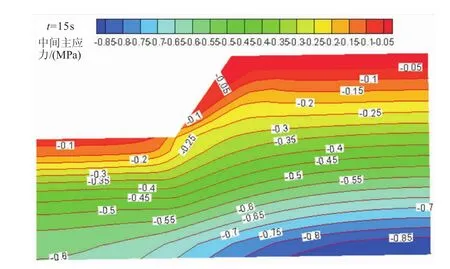
图10　t=15 s时边坡的应力场（中间主应力）Eig.10 Intermediate principal stress field of the cutting slope output at 15 s

由图9、图10和图11可见，随着边坡深度的增加，最大主应力值增大，在计算模型范围以内，最大主应力最大值为-1.5 MPa，出现在边坡模型底端，最大主应力最小值出现在坡顶及其后缘，仅为-0.1 MPa；中间主应力的最大值为-0.85 MPa，与最大主应力相比，其应力值要小得多，边坡各个部位的中间主应力约为最大主应力的50%，而中间主应力同最小主应力相差不大。

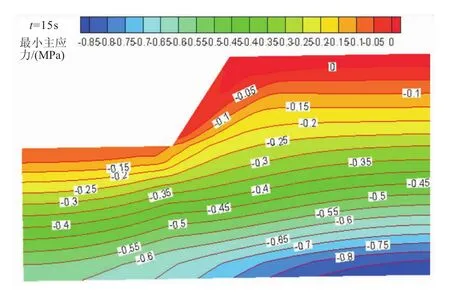
图11　t=15 s时边坡的应力场（最小主应力）Eig.11 Minimum principal stress field of the cutting slope output at 15 s

3　遗传算法应用

在得到不同时刻动力有限元应力场计算结果后，将应力场代入MATLAB编写的遗传算法程序，一方面能够得到边坡安全系数时程曲线，另一方面能够智能搜索边坡临界滑动面，并求出相应临界滑动面包络线的安全系数。

3.1遗传算法

遗传算法最早由美国学者John［12］提出，该算法通过智能自适应搜索来模拟生物进化的过程。1998年，我国学者肖专文等［13］最早将遗传算法应用于边坡工程稳定性计算，从而引发了国内岩土工程界对遗传算法的研究热潮。遗传算法的数学模型为

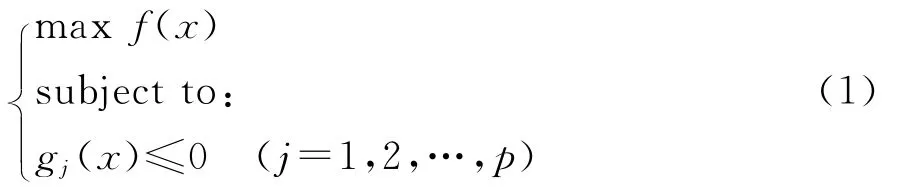
式中:f（x）为目标函数；gj（x）为约束函数；x为目标种群的基因；p为目标种群的数目。

其中:

式中:Cmax为可以采用当前g（x）出现过的最大值，但最好与群体无关。

遗传算法智能搜索步骤如图12所示。

3.2遗传算法应用于边坡稳定性分析的步骤

运用遗传算法求解边坡的安全系数时，需要自动搜索的目标为边坡临界滑动面、最小安全系数。目标函数f（x）为临界滑动面对应的安全系数；约束函数gj（x）为过浅、太尖、锯齿状不良滑动面，需要将其过滤处理；目标种群的基因x为边坡滑动面的深度向量。在得到动力有限元应力场计算结果后，运用遗传算法智能搜索边坡临界滑动面及计算其安全系数的步骤如图13所示。

图12　遗传算法智能搜索流程图Eig.12 Elow chart of intelligent search based on genetic algorithm

图13　遗传算法智能搜索边坡临界滑动面及计算其安全系数流程图Eig.13 Elow chart of the intelligent search of critical slip surface and the calculation of its safety coefficient based on genetic algorithm

3.3遗传算法计算边坡安全系数

把动力有限元计算得到的不同时刻应力场结果代入MATLAB编写的遗传算法程序后，可得到边坡安全系数时程曲线，见图14。

由图14可见，在计算时间40 s内，边坡安全系数不是定值，而是随着地震波加速度的变化而不断波动:在t＜10 s时，边坡安全系数波动幅度较大，出现了6次峰值，这个时间段内的边坡安全系数出现最大值、最小值；在t＞15 s后，边坡安全系数波动幅度放缓，边坡安全系数基本在1.6附近波动。可见，边坡安全系数时程曲线较好地反映了各个时间段地震动力荷载作用下的边坡安全系数。

图14　边坡安全系数时程曲线Eig.14 Time history curve of the safety coefficient of the slope

3.4遗传算法智能搜索边坡临界滑动面

遗传算法智能搜索边坡临界滑动面的第一步是生成初始群体，为了确保计算精度，需保证样本多样性，也即保证初始样本数量足够大。本文按照一定的比例选取了不同的滑动面进行迭代计算，其中优秀基因与劣等基因的比例为40%∶60%。

通过评价函数fi=a（1-a）i（a为评价参数，i为滑动面的排列序号）对所选取的滑动面的优劣进行评价，滑动面安全系数小即为优等滑动面，反之为劣等滑动面。

在遗传算法智能搜索边坡临界滑动面过程中，需要对遗传算法进行搜索控制，也即对种群中不重复的独立基因进行控制，以通过调整优等、劣等基因的被选择概率的比值来达到控制的目的。本文在试算后，发现在循环迭代500次时，其优劣基因被选择概率的比值等于10，此时能够保证独立基因维持在较高的水平，且越是在搜索后期，独立基因才缓慢下降，其优势基因开始明显增多。

在地震动力荷载作用下，不同时刻对应着不同临界滑动面的安全系数，这些不同临界滑动面的全部包络线为:式中:代表t时刻地震荷载作用下的边坡临界滑动面。

由此得到本文路堑边坡的潜在滑动面包络线见图15。由图15可见，边坡滑动面包络线的安全系数fs在［1.15，1.93］之间，在此范围内边坡存在多条潜在滑动面，各滑动面分布较为均匀，具有明显的分级现象，表明通过遗传算法智能搜索的边坡临界滑动面基本为优等滑动面，计算结果具有较高的精度。

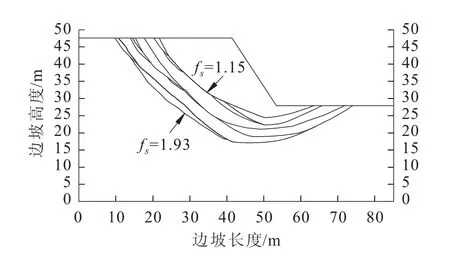
图15　路堑边坡的潜在滑动面包络线Eig.15 Potential sliding surface envelope of the cutting slope

4　结 论

通过动力有限元及遗传算法对地震荷载作用下路堑边坡的安全系数进行研究，得到以下结论:

（1）研究区内路堑边坡典型玄武岩残坡积土的物理力学性质试验结果表明，边坡土体液塑限、含水率较高，液性指数较小，其含水率有较大范围的波动，这对坡体稳定性判定产生不利影响；原状土体在达到峰值剪切强度后，沿着断裂面开始破坏，表明该土体具有明显峰值强度，能够为接下来边坡稳定性计算提供依据。

（2）采用ABAQUS有限元程序对路堑边坡地震响应进行计算，将程序输出的位移场用来分析坡顶位移变化，将得到的加速度用来计算加速度分布系数。动力有限元分析结果表明:输入地震波加速度0.2 g后，坡顶相对位移不断波动，在40 s计算时间内整体呈增长趋势，且其波动趋势与地震加速度较为吻合，尤其是加速度突变时，坡顶相对位移也随即发生突变。

（3）将动力有限元输出的应力场代入遗传算法程序，计算边坡安全系数时程曲线，并智能搜索边坡临界滑动面。计算结果表明:在计算时间40 s内，边坡安全系数不是定值，而是随着地震波加速度的变化而不断波动；搜索得到的边坡滑动面包络线的安全系数在［1.15，1.93］之间，在此范围内，边坡存在有多条潜在滑动面，各滑动面分布较为均匀，具有明显的分级现象。

（4）本文基于动力有限元并结合遗传算法，将各个时刻边坡的应力场代入遗传算法程序，同时用遗传算法程序智能搜索边坡临界滑动面，得到各个时刻相对应的边坡安全系数，相比较传统的拟静力及固定圆弧滑动面分析法，该方法体现了地震荷载时程特征效应，得到了不同时刻的边坡临界滑动面及其安全系数包络线，其计算结果更加丰富，且准确、实用。

［1］闫中华.均质土坝与非均质土坝稳定安全系数极值分布规律和电算程序简介［J］.水利水电技术，1983（7）:9-15.

［2］孙君实.条分法的数值分析［J］.岩土工程学报，1984，6（2）:1-12.

［3］Nguyen V U.Determination of critical slip surface［J］.Journal of Geotechnical Engineering，ASCE，1985，111:238-251.

［4］陈祖煜.土质边坡稳定分析［M］.北京:中国水利水电出版社，2005.

［5］夏元友，李新平，程康.用人工神经网络估算岩质边坡的安全系数［J］.工程地质学报，1998，6（2）:155-159.

［6］Goh A T C.Genetic algorithm search for critical slip surface in multi-wedge stability analysis［J］.Canadian Geotechnical Journal，1991，36（2）:383-391.

［7］傅鹤林，彭思甜，韩汝才，等.岩土工程数值分析新方法［M］.长沙:中南大学出版社，2006:68-140.

［8］中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.GB 50011—2001 建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［9］刘晶波，谷音，杜义欣.一致黏弹性人工边界及粘弹性边界单元［J］.岩土工程学报，2008，28（9）:1070-1075.

［10］杨超，董立山，申俊敏，等.边坡矢量和分析法最危险滑面搜索研究［J］.安全与环境工程，2014，21（3）:28-35.

［11］李翔，程聪.基于数值模拟的滑带土蠕变特性研究［J］.安全与环境工程，2014，21（4）:25-29.

［12］康永君.地震作用下边坡安全系数时程计算方法及应用研究［D］.北京:清华大学，2009.

［13］肖专文，张其志，梁力，等.遗传进化算法在边坡稳定性分析中的应用［J］.岩土工程学报，1998，20（1）:44-46.

Safety Factor Calculation of Cutting Slopes under Earthquake Action Based on Dynamic Finite Element Method and Genetic Algorithm

YU Qingfeng1，2，WU Li1，LI Yinian2，LIU Wengang3，WANG Xiandeng4
（1.Faculty of Engineering，China University of Geosciences，Wuhan 430074，China；2.Hubei Province Communications Planning and Design Institute，Wuhan 430051，China；3.Jiangsu Province Communications Planning and Design Institute Limited Company，Nanjing 210014，China；4.Wuhan Municipal Engineering Design and Research Institute Co.，Ltd.，Wuhan 430023，China）

Eor the purpose of studying the cutting slope stability and sliding characteristics under the seismic dynamic load，this paper firstly does the indoor experiment to study the physical and mechanical properties of weathering basalt residual soil which has been sampled from Jiaoyang-Chengguan highway，and obtains the physical and mechanical index of plastic limit water content，shear strength of typical slope soil body fluids in the study area. Then the paper applies the test results of parameters in ABAQUS finite element program to calculating the earthquake response of the cutting slope applies the displacement field output from the program to analyzing the slope displacement changes，and applies the output of the acceleration to calculating the acceleration distribution coefficient and the output of the the dynamic finite element stress field from genetic algorithm program programed by MATLAB to calculating the safety factor time history curve of a slope.Eurthermore，the paper intelligently searches the critical slip surface of slope.Einally，the study obtains the rules of safety factor as the change of seismic acceleration and the safety factor of sliding surface envelope.

cutting slope；seismic dynamic load；safety factor；dynamic finite element method；genetic algorithm

X43；TU457

A

10.13578/j.cnki.issn.1671-1556.2015.05.003

1671-1556（2015）05-0013-07

2014-12-15

2015-01-14

国家自然科学基金项目（41402259）；湖北省自然科学基金重点项目（2013CEA110）

余庆锋（1980—），男，博士研究生，工程师，主要从事岩土工程与地下建筑等方面的研究。E-mail:113287337@qq.com