刀盘掘进过程动态仿真

韩美东，曲传咏，蔡宗熙，金立帅

(天津大学机械工程学院，天津300072)

隧道掘进机(tunnel boring machine，TBM)是隧道掘进的专门工程机械，被广泛用于地下交通、运输管道等隧道工程建设。作为TBM开挖岩石的关键部件，刀盘性能将直接影响施工效率与安全。目前国内外学者已从刀具破岩机理、刀盘结构设计方法以及刀盘载荷估算方法等方面对TBM刀盘进行了大量研究［1-4］。限于开挖界面的隐蔽性以及施工环境的复杂性，通过传统的理论分析、试验模拟以及工程验证等手段都很难得到理想的研究结果，致使有关TBM刀盘整体的动态掘削及其与围岩相互作用过程的系统研究很少。

近年来迅速发展的数值仿真理论和计算机技术为复杂岩机相互过程的研究提供了新途径。很多研究者在这方面做了大量的工作。文献［5］利用离散单元法(discrete element method，DEM)方法模拟了盾构机掘削土体过程，该方法能够客观反映土体失效面的产生，但由于DEM模型参数的选取还没有较为稳定、有效的方法［6］，致使其应用存在一定的局限。文献［7］基于子模型方法与任意拉格朗日-欧拉有限元方法(arbitrary Lagrange-Euler，ALE)，建立了盾构机刀盘掘削过程的三维数值模型，较好的解决切削过程中网格的大变形问题，但其计算时间较长，占用了大量的计算资源。文献［8］采用直接数值模拟方法对盾构刀盘的掘进过程进行了仿真分析，给出了系统的动态掘进载荷。上述研究有效验证了数值模拟方法在复杂岩机相互作用过程研究中的可行性。然而上述研究的对象为盾构刀盘，考虑到TBM刀盘与盾构刀盘在结构型式、掘削对象上的差异，将数值模拟方法应用于TBM刀盘掘进仿真时需加以改进。

在TBM刀盘掘进仿真方面，当前的研究主要集中在模拟滚刀与岩石的相互作用方面。文献［9］利用有限差分法建立了刀具破岩的二维数值仿真模型，较好地模拟了岩石裂纹生成与扩展情况。但限于二维模型，其仿真结果无法直观形象的反映刀具破岩的动态过程。文献［10］探究了在ANSYS-LS/DYNA环境下建立单把刀具三维破岩仿真模型的方法，并给出了刀具的切削力。目前尚无文献建立考虑完整结构的TBM刀盘破岩的仿真模型。鉴于此，本文将探索一套考虑整盘刀具的TBM刀盘掘进全物理过程的仿真方法，为施工环境下刀盘掘削性能的研究提供有效手段。

1 数值仿真模型

1.1 岩石材料模型

岩石材料模型选用文献［11］中扩展的Drucker-Prager非线性弹塑性本构模型。与常用的Mohr-Coulomb模型相比，扩展的Drucker-Prager模型考虑了中间主应力及静水压力对材料屈服面的影响，方程如下:

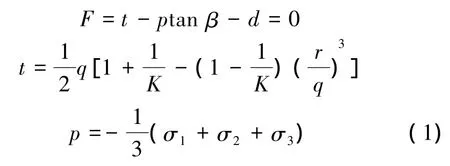
式中:r为偏应力张量的第三不变量;K为与三轴拉伸屈服应力与三轴压缩屈服应力的比值相关的材料参数，0.778≤K≤1;d为凝聚力;β为摩擦角;q为Mises等效应力;p为平均压应力。

1.2 单元损伤失效模型

隧道挖掘是通过滚刀碾压掌子面岩体，掌子面不断向前推进的过程。该过程可以简化为一个岩体切削过程，切削过程最主要的是模拟切削分离，本文将采用文献［11］中包含单元删除功能的单元损伤失效模型来对其进行模拟。

单元损伤失效是为描述损伤对于材料刚度衰减的影响而提出的。基于特定本构关系的单元材料在达到屈服以后，按照一定规律降低单元刚度直至承载能力全部消失。如图1所示，单元损伤失效包含3个阶段:单元未产生损伤时的材料响应曲线AB段、初始破环点B点(由初始损伤准则判定)、损伤演变曲线BC段。

图1 损伤失效模型应力－应变响应曲线Fig．1 Stress-strain curve with progressive damage degradation

当ωs达到1时，材料达到初始破坏点B点;此后，单元刚度开始衰减直至丧失承载能力。

引入刚度衰减变量D对损伤进行描述(D为塑性应变的一个函数)。初始损伤产生后，任意时刻材料的应力张量可表示为

当D=1时，单元刚度完全退化，材料失去承载能力，单元从模型中删除。

1.3 有限元模型

以某型号TBM刀盘为研究对象，根据二维设计图纸，经过适当简化(删除了不影响结构强度的螺栓孔、泡沫注入口、倒角、拐角等微小细节)，建立其有限元模型(如图2所示)。

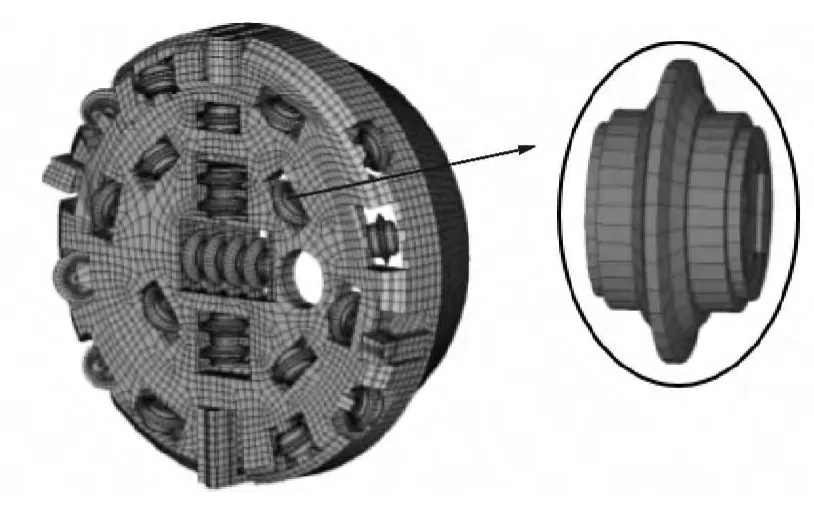
图2 刀盘有限元模型Fig.2 Finite element model of cutter head

模型主要信息如下:

1)刀盘直径4 000 mm，材料为Q345钢;

2)刀盘面板上装配正滚刀9把，边滚刀8把，中心刀1组(由8把滚刀组成)，滚刀直径432 mm;

3)整体模型采用六面体八节点缩减积分单元来划分网格，节点总数为 40 227，单元总数为25 523。

在刀盘周围装配待开挖岩体，形成TBM刀盘切削岩体的整体有限元分析模型(如图3所示)。为得到较好的计算精度并兼顾计算效率，将仿真过程中与滚刀直接接触的岩体网格加密，未与刀盘直接作用的岩体网格适当加大。

岩体的基本材料参数依据文献［12］给定:密度ρ=2.5 × 10-6kg/mm3，泊松比μ= 0.3，弹性模量E=27.6 GPa，内聚力c=25.1 MPa，摩擦角φ=53°。

图3 整体仿真模型Fig.3 Whole simulation model

2 基于显式算法的刀盘掘进过程仿真

2.1 显式积分算法基本理论

TBM刀盘掘进是一个有着连续的动态接触关系、包含材料的破坏和失效的复杂动态过程。本文利用ABAQUS软件的显式动力学分析模块对其进行模拟。

显式求解方法用中心差分方法对时间进行积分，求解其显式运动方程，不需要对刚度矩阵进行多次分解和迭代，从而避免了对于高度材料非线性、高度几何非线性或模型规模较大的动力学问题常常遇到的无法收敛问题。

在时间段开始时(t时刻)，求解整个变形体系统的动力平衡方程:

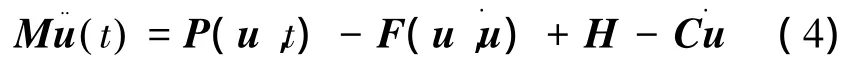
式中:M为节点质量矩阵，u、u˙、u¨分别为节点位移、速度和加速度，P为总载荷矢量，H为总体结构沙漏粘性阻尼力，C为阻尼矩阵，F为单元内力。

在当前时间段开始时(t时刻)的加速度为

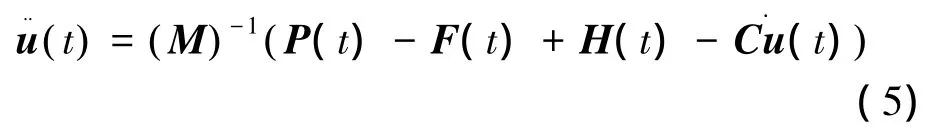
加速度是由中心差分法的时间积分得到的，即假定加速度为常数以求得速度的变化，用这个速度的变化值加上前一个时间段中点的速度来确定当前时间段的中点速度:

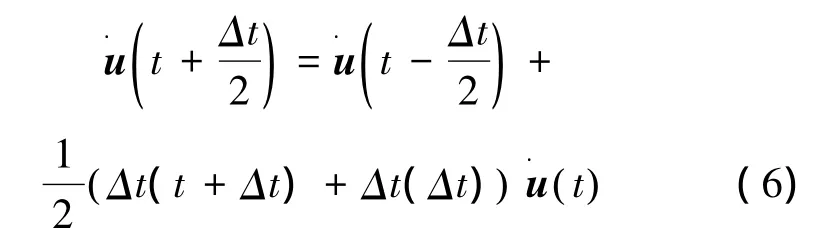
式中:Δt为时间间隔。

速度沿时间积分的结果加上此时间段开始时的位移，即为时间段结束时的位移:

由于方程的求解是非耦合的，不必同时求解联立方程，因此大大节省了求解时间和存储空间。

2.2 关键仿真技术

TBM主要采用滚刀碾压方式破岩，刀具与前方岩体存在连续的动态接触关系。为此，在模拟中将每把滚刀与其前方岩体设定为独立非光滑接触对(由于滚刀刚度较大，故设定其外表面为主动面，岩石表面为从属面);应用罚函数接触方法强化接触约束，并选择罚函数刚度建立接触力与侵彻距离之间的关系;同时，为保证刀具与岩体只在压紧状态下传递法向压力，设定其法向行为为硬接触;鉴于刀盘的旋转运动，滚刀与岩体之间存在较大的相对运动，分析中选用有限滑移公式控制接触面的滑移量。

在实际施工中，TBM刀盘旋转切削岩体的同时受到后方液压千斤顶的顶进作用，以缓慢速度向前推进。鉴于此，本文施加的载荷和位移边界条件可总结如下:1)初始状态刀盘与岩体即将接触;2)刀盘的旋转速度为10 r/min;3)刀盘的推进速度为80 mm/min;4)仿真时间为21 s:0～3 s刀盘转速和推进速度以光滑加载方式由零增加到最终值;3～21 s刀盘转速和推进速度维持恒定，在该时间段内刀盘环向切割岩体3圈。5)约束岩体模型外边界的位移自由度，保待开挖表面为自由表面。

为降低计算成本，分析中对刀盘单元施加刚性约束;同时，为限制数值震荡，改进模拟效果，分析中为模型引入了体粘性，并设定线性体粘性阻尼系数为 0.06、二次体粘性阻尼系数为 1.2。

3 仿真结果分析

3.1 岩体失效分析

由刀盘结构可以看出，滚刀始终高于刀盘面板，在掘进过程中滚刀首先与掌子面接触并成为整个切削过程的主体。初始掘进阶段，在滚刀推力作用下，掌子面岩体发生了弹性变形;随着切深的增加，应力值相应增大，由于岩石为脆性材料，在极短的时间内，岩石发生塑性变形;当达到强度极限后(对应于图1中的B点)，滚刀正前方岩体开始产生局部损伤(如图4所示)。

损伤发生后，岩体刚度开始衰减，应力状态由式(3)决定。随着刀盘的旋转掘进，滚刀与岩体相互作用增强，损伤程度加剧，当损伤变量D的值达到1时，(对应于图1中的C点)，相应岩体因完全失去承载能力而被剥离删除，在掌子面上形成了与滚刀切削轨迹相匹配的一系列同心圆沟槽(如图5所示)，该形貌与文献［13］的描述相吻合。

刀盘掘削不断深入，当推进距离达到8.5 mm时，岩体损伤区域由局部扩展至整个掌子面(如图6所示)，待开挖岩体的承载能力全面降低直至失效剥离，刀盘完成一次破岩。

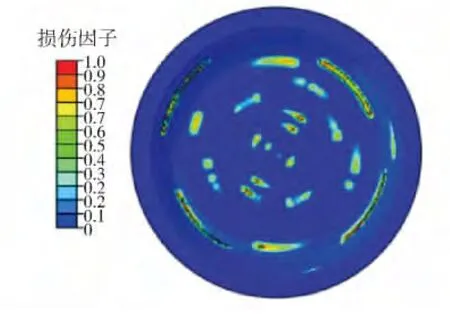
图4 t=2.224 s时岩体损伤云图Fig.4 Damage contour of rock when t=2.224 s

图5 t=4.887 s时岩体形貌Fig.5 Morphology of rock when t=4.887 s

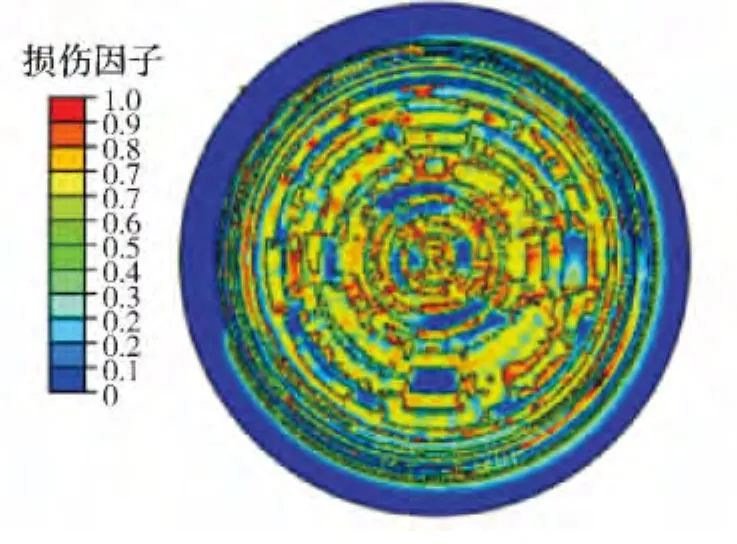
图6 t=7.844 s时岩体损伤云图Fig.6 Damage contour of rock when t=7.844 s

3.2 刀盘载荷分析

载荷是TBM刀盘地质适应性设计及机械动力系统顺应性设计的理论基础，同时也是掘进过程中驱动与传动系统控制的主要依据。本文通过仿真计算得到了TBM破岩过程中刀盘载荷随掘进时间的变化曲线。

如图7、图8所示，伴随刀具滚压破岩，刀盘产生强烈振动，刀盘载荷波动范围较大。在掘进的初始阶段，滚刀与岩石开始接触，接触面匹配不佳，且操作参数不断调整，刀盘掘进载荷呈现出较大波动;9 s后(刀盘旋转1周)，伴随岩体剥离，刀具与前方岩体形成较好的接触关系，且操作参数维持稳定，刀盘进入稳定掘进阶段。该阶段刀盘扭矩的平均值为541 kN·m，最大值为4 147 kN·m;推力的平均值为1 466 kN，最大值为6 019 kN。对稳定段的载荷数据进行快速傅氏变换，设定采样频率为1 kHz，得到其幅频曲线如图9、图10所示。

图7 刀盘扭矩时程曲线Fig.7 Curve of torque with time

图8 刀盘推力时程曲线Fig.8 Curve of trust with time

图9 扭矩幅频曲线Fig.9 Amplitude-frequency curve of torque

图10 推力幅频曲线Fig.10 Amplitude-frequency curve of driving force

对载荷的幅频数据做进一步分析，得到峰值较大处扭矩和推力的幅频信息如表1所示。表1显示:在掘进稳定段，扭矩和推力的各阶主频均相同;载荷的第1阶主频(峰值点A对应的频率)约为刀盘转动频率的2倍(刀盘转速10 r/min，即转动频率为0.167 Hz)。进一步分析表1可知，刀盘载荷存在高频成分(峰值点D)，其频率与刀盘转动频率的比值约为36，该数值恰为刀盘安装刀具数量(正滚刀9把、边滚刀8把、中心刀1组，共18把)的2倍。由此推测，刀盘载荷的高频成分或与刀盘安装刀具的数量相关。

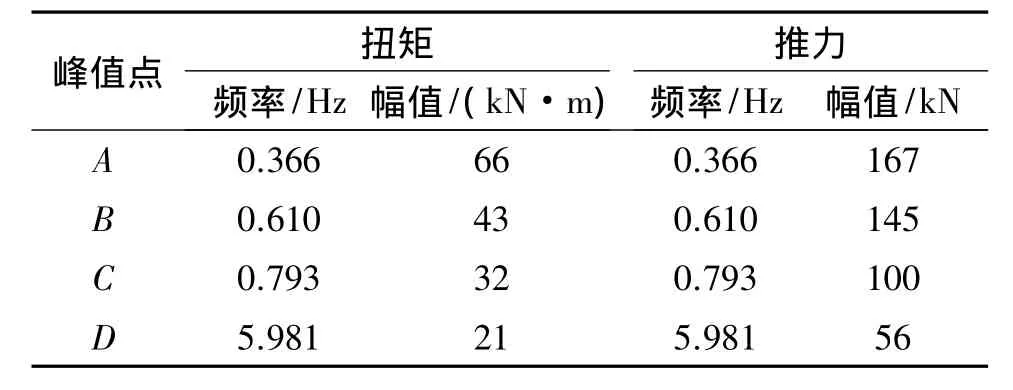
表1 峰值点处载荷的幅频信息Table 1 Amplitude-frequency information of loads at the peak points

4 结论

1)建立了TBM刀盘三维破岩仿真模型，应用包含单元删除功能的损伤失效准则模拟切削的形成和分离，实现了刀盘掘进过程的直接数值模拟。

2)模拟了刀盘掘进过程中掌子面岩体由损伤初始到失效剥离的完整演化过程:初始阶段，滚刀在刀盘推力和扭矩的共同作用下，在掌子面上切出一系列同心圆沟槽，该现象与实际工况相吻合;当推进距离达到8.5 mm时，掌子面岩体全面损伤，刀盘进入稳定掘进阶段。

3)分析得到了刀盘的动态掘进载荷，其值波动剧烈;在掘进稳定段，推力与扭矩主频相同，其第1阶主频约为刀盘转动频率的2倍。

4)刀盘载荷的高频成分或与刀具数量存在相关性。

上述结果表明，本文建立的模拟方法能较好的模拟TBM掘进过程中刀盘与围岩的相互作用过程，可以为TBM刀盘掘削性能的研究提供一种有效方法。

［1］GERTSCH R E.Rock toughness and disc cutting［D］.Rolla:University of Missouri，2000:1-256.

［2］刘志杰，滕宏飞，史彦军，等.TBM刀盘设计若干关键技术［J］.中国机械工程，2008，19(16):1980-1985.LIU Zhijie，TENG Hongfei，SHI Yanjun，et al.Cutterhead design key issues of a full face rock tunnel boring machine(TBM)［J］.China Mechanical Engineering，2008，19(16):1980-1985.

［3］ROSTAMI J，OZDEMIR L，NILSON B.Comparison between CSM and NTH hard rock TBM performance prediction models［C］//Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling Technology.Las Vegas，USA，1996:1-10.

［4］张宁川.硬岩掘进机刀盘纯切削扭矩计算研究［J］.隧道建设，2008，28(6):638-641，645.ZHANG Ningchuan.Study on cutting torque calculation of cutterhead of hard rock TBMs［J］.Tunnel Construction，2008，28(6):638-641，645.

［5］MAYNAR M J，RODRÍGUEZ L E.Discrete numerical model for analysis of earth pressure balance tunnel excavation［J］.Journal of Geotechnical and Geoenvironmental Engineering，2005，131(10):1234-1242.

［6］ASAF Z，RUBINSTEIN D，SHMULEVICH I.Determination of discrete element model parameters required for soil tillage［J］.Soil and Tillage Research，2007，92(1):227-242.

［7］沈建奇，金先龙，杨建刚，等.盾构机刀盘掘削动态数值模拟［J］.上海交通大学学报，2009，43(6):1017-1020.SHEN Jianqi，JIN Xianlong，YANG Jian’gang，et al.Dynamic numerical simulation of excavation in shield tunneling［J］.Journal of Shanghai Jiao Tong University，2009，43(6):1017-1020.

［8］苏翠侠，王燕群，蔡宗熙，等.盾构刀盘掘进载荷的数值模拟［J］.天津大学学报，2011，44(6):522-528.SU Cuixia，WANG Yanqun，CAI Zongxi，et al.Numerical simulation of excavation load on cutterhead in shield tunneling machine［J］.Journal of Tianjin University，2011，44(6):522-528.

［9］GONG Q M，ZHAO J，HEFNY A M.Numerical simulation of rock fragmentation process induced by two TBM cutters and cutter spacing optimization［J］.Tunnelling and Underground Space Technology，2006，21(3-4):263-270.

［10］谭青，张魁，夏毅敏，等.TBM刀具三维破岩仿真［J］.山东大学学报:工学版，2009，39(6):72-77.TAN Qing，ZHANG Kui，XIA Yimin，et al.Three-dimensional simulation of rock breaking by TBM cutter［J］.Journal of Shandong University:Engineering Science，2009，39(6):72-77.

［11］Hibbitt，Karlsson and Sorensen，Inc.ABAQUS analysis user＇s manual help online［M］.［S.l.］:SIMULIA，2005:1-679.

［12］满林涛.盘形滚刀破岩过程有限元数值模拟［D］.大连:大连理工大学，2012:1-67.MAN Lintao.Numerical simulation of rock breaking process by disc cutter using finite element method［D］.Dalian:Dalian University of Technology，2012:1-67.

［13］宋克志，王本福.隧道掘进机盘形滚刀的工作原理分析［J］.建筑机械，2007，(4):71-74.SONG Kezhi，WANG Benfu.Operation principle analysis of disc cutter on TBM［J］.Construction Machinery，2007，(4):71-74.