基于RSA的门限密码体制研究

张久辉 左明鑫

（1.郑州电力职业技术学院 电力工程系，河南 郑州451450；2.郑州科技学院 电气工程学院，河南 郑州450064）

1 概述

现代密码学技术在私钥没有泄露的情况下基本上可以做到完善保密，也就是说偷窥者无法在可以接受的时间内将密文翻译成明文。有时候，我们为了防止权力的过分集中，常常采用密钥分散管理。所谓密钥分散管理，就是把一个系统密钥S分成N个密钥碎片S1，S2，…，Sn，并且分发给N个具有合法性的节点P1，P2，…，Pn［1］，给定一个正整数T，且T＜N，在任何成员数t＜T的情况下都不能由他们的部分秘密中得到整个系统的秘密，只有当成员数t＞T的情况下合作才可以完成密码运算，从而很好地解决了权力过分集中的问题。在某些不便频繁更换密钥的场合，密钥自身的安全性至关重要，如何提高密钥的安全性成了很多人研究的课题，本文将介绍所采用的具体加密算法。

2 密钥碎片的生成

首先需要存在一个可靠的认证中心CA［2］，所谓可靠，就是假设这个CA是安全而不容易被攻破的，以及CA不会对系统信息构成威胁，这里的CA就好比大会选举中的唱票人员，左右不了大会的投票结果。CA采用如下的方式进行密钥碎片的生成，具体可以描述为：CA首先要建立一个矩阵A=［aij］NXn（其中i，j都是正整数，1≤i≤N，1≤j≤n）和一个列向量B=［bj］TX1，且n＞T，我们任取矩阵A中的任意T列组成的新矩阵A就可以和列向量B相乘得到一个列向量C=AB=［cj］Nx1，C就是N维向量空间里的一个元素，C就是由所有C组成的集合，所以C中应该共有个元素。矩阵和向量乘积可以用如下公式表示：

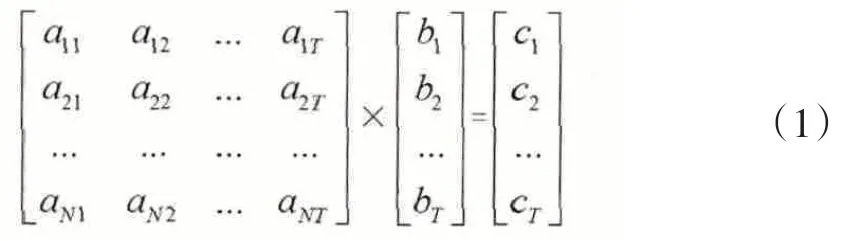
认证中心CA就把向量A中的每个列向量作为一个密钥碎片S1，S2，…，Sn安全地发送给n个合法的节点P1，P2，…Pn。

3 密钥碎片的分发

至于如何安全地将密钥碎片发送到合法用户手中，有很多种方法（包括硬件的或软件的），由于椭圆曲线加密算法ECC［3］具有较高的安全性和难破译性，本文采用椭圆曲线的方法将密钥碎片发送给合法用户。这里就需要每个合法节点用户建立一个自己的公私钥对［4］，认证中心CA用户节点的公钥对要发给用户节点的密钥碎片进行加密，用户节点再用自己的私钥对认证中心发过来的密钥碎片进行解密。假设某个节点的椭圆曲线方程为y2=x3+x+6，私钥为t=9，公钥a=（2，7），b=9a=（10，9），具体用公式描述加密解密过程如下：

加密过程

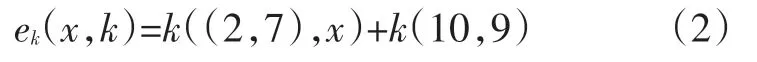
解密过程

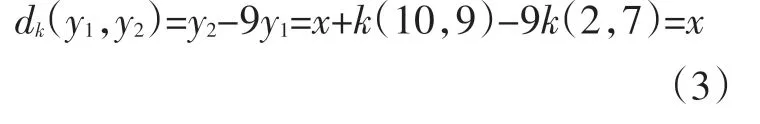
当需要改变某些节点的权利时，我们只需要相应地改变矩阵A的列向量数及其内容。比如要去掉第i个节点的权限，只需要认证中心CA去掉矩阵中的第i个列向量，同时集合C中的列向量数也要做相应地调整。在投票后，认证中心CA将收到的密钥碎片和矩阵A的列向量进行对照，在矩阵A中不存在的列向量都被认为是无效的。当需要增加一个或几个合法用户节点的权限时，我们只需要简单地在矩阵A中增加一个或几个列向量，只要满足增加的列向量aNj和列向量B的乘积数和C中的任一元素都不相等即可。然后用解密后的密钥碎片组成一个新的矩阵A，再用矩阵A和列向量B相乘，把所得的列向量C与列向量C中的元素进行对照，如果满足集合C≤C，则投票完成。从而可得，任何小于T个密钥碎片都不能完成上面的矩阵乘法，也就是说小于T个合法节点都无法进行投票。

4 会话机制的建立

在合法节点与认证中心通信时，通信内容往往会被窃听，为了保证通信内容的安全性，需要对节点发送给认证中心的密钥碎片进行加密，这就是多级加密中的二级加密思想。采用RSA密码体制对各点的密钥碎片进行加密，各合法用户节点用认证中心CA的会话公钥对自己拥有的私钥碎片中每个元素逐个进行加密。

设n=pq，其中p和q为大素数。且定义K=｛（n，p，q，a，b）：a b≡1（modØ（n））｝，其中n和b组成了公钥，且p，q和a组成了私钥，当需要投票时，节点Pi用公式（6）对密钥碎片中的每个元素逐个进行加密，然后把加密后的数据发送给认证中心CA，认证中心收到节点Pi发送过来的数据后用公式（7）逐个进行解密［5］。

由

得

加密过程

解密过程

认证中心把从各个节点Pi发送过来的正确密钥碎片经解密后，把这些密钥碎片随机组成一个矩阵A1，当A1的列向量数大于等于T时，任取其中T列组成新的矩阵A2，然后看A2与列向量B乘积C1是否属于C，如果属于C则投票完成，如果不属于C，我们就重新选取A1中的元素T列，再与列向量B乘积，只要有一次乘积结果是C中的一个元素，投票就算完成。只有所有次选取组成的向量与B乘积都不是C中的元素时，不能打开系统秘密。

5 结语

采用多方协商的方式，使用密钥分散管理能很好地解决权力过分集中和密钥不便经常改变的问题，能够抵抗中间人的攻击，能改变合法用户权限。但是对系统内部的攻击却很薄弱，这几乎是现在信息安全方面的一个通病，再一个是过分依赖认证中心，如果认证中心不可靠，整个系统就没秘密可言。

［1］Zhou L and Haas Z J，Securing ad hoc networks［J］.IEEE network，special issue on network security，November/December，1999.

［2］Ratna Dutta，Sourav Mukhopadhyay，Martin collier Computationally secure self-healing key distribution with revocation in wireless ad hoc networks［J］.Contents lists available at Science DirectAd Hoc Networks2010：15-17.

［3］ELGamal，Principle and Practice of Cryptograhy［M］.Beijing：Electronic Industry Press，2009：184-186.

［4］Chen kefei，Threshold RSA Cryptosystem［J］.ACT ELECTRONICASINICA，1999，27（6）：1-2.

［5］N Koblitz.Elliptic curve cryptosystems［J］.Math.Comp，1987，177（48）：203-209.