钢在塑性变形加工阶段所呈现的物理性能分析

魏 凯 焦政华 王艳艳

（河南安阳钢铁集团有限责任公司，河南 安阳455004）

金属材料常见的塑性变形主要有轧制（棒材、板材、管材、线材及型材）、挤压（有色金属、低碳钢）、拉拔（有色金属、碳钢等型材、线材及管材）、锻压（合金钢、碳钢及特种钢胚料）、冷冲压（合金钢板材、低碳钢）四种，本文主要对钢的塑性变形成的物理性能进行研究。

1 塑性变形概念

塑性变形是指金属材料在加工及使用过程中受到的外力，在塑性变形中通常要经历弹性变形、弹塑两性变形和断裂三个阶段。在晶界作用下，金属塑性变形可出现阻力增大；在晶粒位向作用下，金属可出现内应力；单位体积内金属晶粒越小，则晶界越多，塑性变形难度越大，可得到细晶强化。金属在承受外力（冲击、静、交变）的作用下时，未出现超过许可变形或者不破坏的能力为金属的力学性能，主要包括塑性、强度、冲击韧性、硬度、疲劳强度等，力学性能指标是选择金属材料的重要依据，有着重要的作用［1］。

钢在接受冷塑性变形时，其外部晶粒形状可沿着变形的方向出现拉长或者压扁现象；内部晶粒位错密度明显增加，晶格出现剧烈畸变；在冷塑性变形时，金属的硬度和强度在一定程度上都会有所提高，在这个时期内其塑性和韧性都会显著地降低，这种现象也被称为“加工硬化”或者“形变强化”。加工硬化是对无法进行热处理强化金属的重要强化手段，有助于材料的抗突然超载能力的提高［2］。通过这种处理，有助于材料的强化、塑性变形的均匀进行，同时有助于金属构件的工作安全性。

2 试验曲线和数值

金属塑性变形时的应力是在不可逆的变形条件下，结合塑性体每一个点的应力和应力变化的物理参数。在塑性本构的公式中，瞬间的变形速度和温度变化会影响应力的大小和应力变化的范围。当变形速度和温度不同时，变形体可以近似地看成是钢塑性体。当今社会，工艺技术迅猛发展，塑性加工技术明显提高，出现了更多的特殊塑性体形状和更加精密的塑性体成形技术，因此在实际进行决定力能参数和数值模拟时，应将特殊塑性体形状和更加精密的塑性体成形技术归入到影响应力变化的参数中［3］。

当刚出现塑性变形时，变形速度和变形的抵抗力在一定程度上会受到应力程度和温度的影响，两者之间存在函数关系。具体假设如下：在变形中的一个瞬间，则两者之间的函数关系式为在这个公式中r指的是温度，ε指的是变形程度，σs指的是材料的屈服应力，其中，T变是变形温度，单位K，T熔为融化温度，单位指的是变形速率［4］。

当出现变形温度不同时，需要进行拉伸试验，目的是将该试验装置能自动测量出盘上的瞬间阻力σs并做好记录，变形伸长量ε、屈服应力σs，拉断时的εk、缩颈时的εw以及曲线。选择以下几种钢进行试验，得出钢的特性值及关系曲线。

对试验得到的关系曲线进行分析，则能够得到σB值自r=0变成r=r0=0.36时，在这个时候进行拉伸，则塑性变形将出现不规则变化现象，会出现“缩颈”失稳。当σB出现最大强度的极限边界点时，塑性变形的强化程度达到顶峰，此时导数是0，得到公式1：

当出现碳钢r＞r0的情况时，也就是r0是在0.4～0.45这个数值范围时，公式的曲线图是向下落的抛物线。当σB=f（r）即在同一个曲线上时，曲线上会出现一个交叉点，即可得到公式2：

当超过这个交叉点后，抛物线的下落走势是平滑的，当r的变化范围是从0.73变到1时，抛物线的变化趋势是平缓走势。当r达到1时，σB与σBk的最小值相等。

根据σB=f（r）的曲线变化特征，如果出现同时改变时，我们可以将这个抛物线看成是六项幂方程式，此时可以得到公式3：

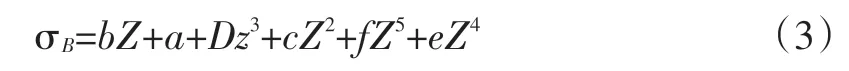
在这个公式中，Z是由r和r0决定的，即，这个公式决定了abcdef这6个系数，因此在计算时应运用到下列数据：r=rC-σB0=σBC，则ə2σB/ər2为0；若r=r0-σB=σB0，则əσB/ər；若r=1-σB=σBK，则əσK/ər为0，将公式（1）分解为6个方程，得到的方程精简后，则可得到公式（4）：

在公式4中，要保证任意条件下均符合，当1≥r≥r0，此时，结合σB0的数值大小，可以同时得到B0、BC、BK和r0的微积分数值大小，当数值确定时，则不能够对得到结果的准确性进行反映。在进行试验时，考虑到碳素工具钢与普通碳素钢之间的差异，rC=0.4～0.45，r0=0.3～0.36，此时将公式（4）带入平均值ZC=0.86，则可得到公式5，公式化简以后变成如下公式：

根据公式5得到σB的试验值和计算值，在r=1、r=r0的条件下，则可得到əσB/ər为0，然而并不包括ZC和σBC的数值。

通过对计算结果进行观察，能够发现，rc=0.4时，可根据公式（5）得到为0，与试验数据存在差异。因此，根据公式（5）进行计算，当数值确定时，任意条件下，也就是r在r0（包含）与1（包含）之间时，需要根据BK、B0和σ的微积分数值大小来决定。

当变形量ε的数值大小不断变大时，σB=f（r）的抛物曲线在应力变化的范围内会出现交叉重合。当r数值不断增加时，σB受到ε的影响明显变小。为了对ε影响σB进行计算，联解σS和σB，则可得到线性方程（6）：

公式（6）中的σB是公式（4）或者（5）的函数，除此之外，还需要了解σw与r之间的关系，通过对图1进行观察，能够发现，当r值在r0之内时，则σW基本无明显变化。

表1 几种钢的特性值

当r=r0时，则εw=f（r）的最小值主要取决于əw/ər=0；当r=rk时，εW=f（r）由əw/ər=0，则此时达到最大值。当r在r0（包含）与rk（包含）之间时，εw=f（r）出现拐点，此时ə2εw/ər=0。

当r在r0与rk之间时，εw=f（r）可参考公式（3）和公式（4）的形式，只需要进行简单的代替，则得到：

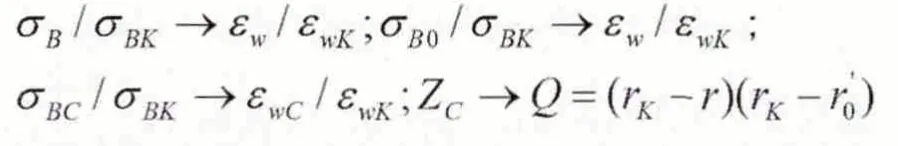
为了得到公式（5）的类似表达，此时采用平均值rc=0.73，可得到Qc=0.34，计算得到公式（7）：

在公式（6）中，当r=rk时，则w=εwk；当r=r0时，则εw=ε0，因此əεw/ər=0。

当r的值是0.73时ə2εw/ər2=0。当出现温度不一样时，塑性体变形的反应程度和流动应力的线性变化都是不一样的，要进行观察，则能够发现r4＞r3＞r2＞r1，随着r数值的变化，直到r=r0，σs=f（ε）自此向下平行交叉，而强化指标E并未出现变化。也就是说E1=E2。当r大于r0时，σs=f（ε）线，当E值不断减小，则E3和E4的走势图是向下交叉，变成E3=E4。

本次实验结果可以得知，通过使用拉伸实验的方式将该试验装置能自动测量出盘上的瞬间阻力σs，从而得出对塑性体真实变化情况的曲线图，其中，变形速度ε对σs的影响是通过幂函数的方程式表示的。我们根据公式6可以得出σs=f（r、ε）函数的具体数学方程式，即得到公式（8）：

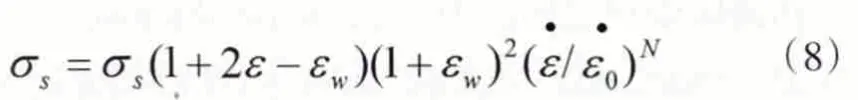
公式中：在一般试验条件下，ε取（5-6）×10-6/s；N为（0.3-1.0）r，εw和εK的变化情况为正比，对公式进行修正之后，可得到（9）。

公式中，φ和φ1，对于一般钢则为φ1为（0.3～0.8）、φ1为（1.05～2.2）。室温下进行塑性变形时，εK则为应力状态指标Ⅱ（Ⅱ=σ平均/σs）的函数，其近似关系见（10）：

根据以下条件则能够得到多次幂的系数：即II为1时，根据əε/əⅡ=0，则得到εk=ε2；当Ⅱ=-1时，ε=ε3，此时如果忽略r对εk和Ⅱ的影响，也就是当r大于r0时，可以得到公式（11）：

公式（11）反映了当r数值不断变化时，ε（r）也跟着变化，而且变化范围是非常大的，也有可能会产生同等距离的变化趋势。

3 结语

对钢进行塑性变形加工，对其材料力学性能、化学性能及物理性能进行改变，是工业需要的常见步骤，为了研究钢在塑性变形加工阶段所呈现的物理性能，本次研究进行了几种钢材料的试验，并得出以下结果：当出现一个新的数学方程式时，我们应该结合变形的速度、温度和程度等对抗力的影响；新的数学方程主要来自于试验曲线，并在此基础上进行了严格的数学推导，进一步提高了试验的科学性。本次讨论内容及研究成果均大大丰富了塑性加工理论。

［1］罗子健.金属塑性加工理论与工艺［M］.西安：西北工业大学出版社，1994.

［2］白井英治，白坚高洋.金属加工力学［M］.北京：国防工业出版社，1984.

［3］潘艳华，邹晋，董应虎.Cu含量及纯度对Mo-Cu合金热物理性能的影响［J］.江西科学，2011（6）：740-744.

［4］郭广文，马惠霞，张健.高碳钢的热物性与显微组织的关系［J］.理化检验物理分册，2006（4）：167-670，186.