基于路径选择的交通拥挤费定价模型研究＊

吴 中，杨 洋 ，马 乐，陶 帅

(河海大学 土木与交通学院，江苏 南京210098)

经济的发展使得交通需求与供给的矛盾日益突出，交通拥挤已成为困扰城市决策者的主要问题。交通拥挤收费的理论最初由Pigou 于上个世纪20 年代提出，近年来一些学者利用数学规划的方法来研究这一问题。文［1］和文［2］利用双层规划和基于灵敏度分析的算法对拥挤道路收费问题进行了研究。文［3］利用双层规划模型与步长加速法和罚函数法组合的启发式算法对弹性需求下的道路收费问题进行了研究，给出了不同路段的收费费率，以求达到网络交通流的平衡，但其方法复杂，难以推广应用。文［4］运用定量和定性的方法探讨了交通拥挤中社会和个人成本的组成，以及两者之间的关系，但未给出应用于实际的计算模型。文［5］在综合考虑流量和成本的关系的基础上，提出了以个体成本总量和社会总成本最小化为目标的多目标模型。但是采用用户均衡交通分配模型，没有考虑用户选择某条路线的效用是随机的特性。本文构建了一个基于多路径选择的交通分配双层规划模型结果，建立的交通拥挤定价模型。针对双层规划模型，采用了Kuhn-Tucker 原理将双层规划模型转化为单层规划问题求解。分析不同拥挤费对交通配流的影响，以达到多路径选择下个体与社会总成本最优的目的。

1 交通拥挤的评价标准

交通拥挤是一个模糊的、难于具体量化的概念。通常用饱和度指标综合反映道路拥挤的程度，故本文是以饱和度作为判断拥挤程度的主要影响因素。具体参考标准如表1［6］。

表1 交通运行状态评价表

2 基于路径选择的交通流分配模型

(p，q)为交通网络中任意OD 对，p ∈Z 为起点编号，q ∈Z 为终点编号，Z 为起讫点集合;Op为起点p 的交通需求发生量;va为路段a 上的交通流量;Ca为路段a 的设计通行能力;Rpq为p 和q之间的路径集合是连接起点p 和终点q 之间第OD 对的r 条路径上的交通流量;表示p 和q 之间路径r 的费用;表示p 和q 之间所有分配到流量的路径中最小的费用;是路段/路径关联系数;dpq表示OD 对之间的交通需求量;ta表示路段a 的费用函数;u 表示拥挤费用;Ta表示路段a 的广义费用，即Ta= ta+ u。

那么，基于路径选择的交通流分配双层规划模型的数学模型如下:

其中上层模型描述城市交通管理部门对拥挤收费的决策，目标是路网综合效能最大，即系统最优，通常用总出行时间最短、社会成本最小等指标来衡量，即:

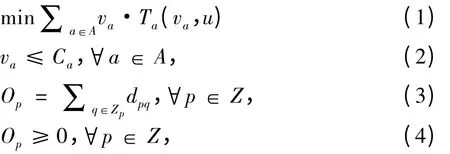
其中，式(2)要求路段a 的交通流量不大于路段a的设计通行能力。式(3)表示各交通区域发生量的约束。

下层模型［7］则描述道路使用者在出行OD 的不同路径之间的选择，采用个人出行时间最短或个人广义出行成本最小等指标来衡量。本文的目标函数在以网络流均衡分配为目标的同时，约定网络中各起点处的交通需求按照Logit 选择模型分配出行终点，即:

其中，θ 是阻抗系数，反映了需求分布对于O-D 间出行费用的敏感性，本文取值为0.75。公式(6)O-D 需求和路径流量之间的转换关系，表明各起点区域的全体出行者自由选择出行终点。公式(7)表示了路径流量和路段流量之间的转换关系。

3 基于路径选择的交通拥挤费定价模型

由基于路径选择的交通流分配模型，可以得到在某一拥挤费下的各个路段的交通量、路段饱和度以及社会成本等信息。根据交通拥挤的评价标准，判断在此拥挤费下的道路的状态。循环此过程，直到得到无论道路饱和度还是社会成本都最小的情况，输出此时的拥挤费用。根据全国高速公路收费标准，每车每公里平均收费1.36 元，一条路段的长度范围大概在1 ～10 公里，因此拥挤费用u 选择范围在1 ～10 元。具体基于路径选择的交通拥挤费定价流程如图1。

4 模型求解

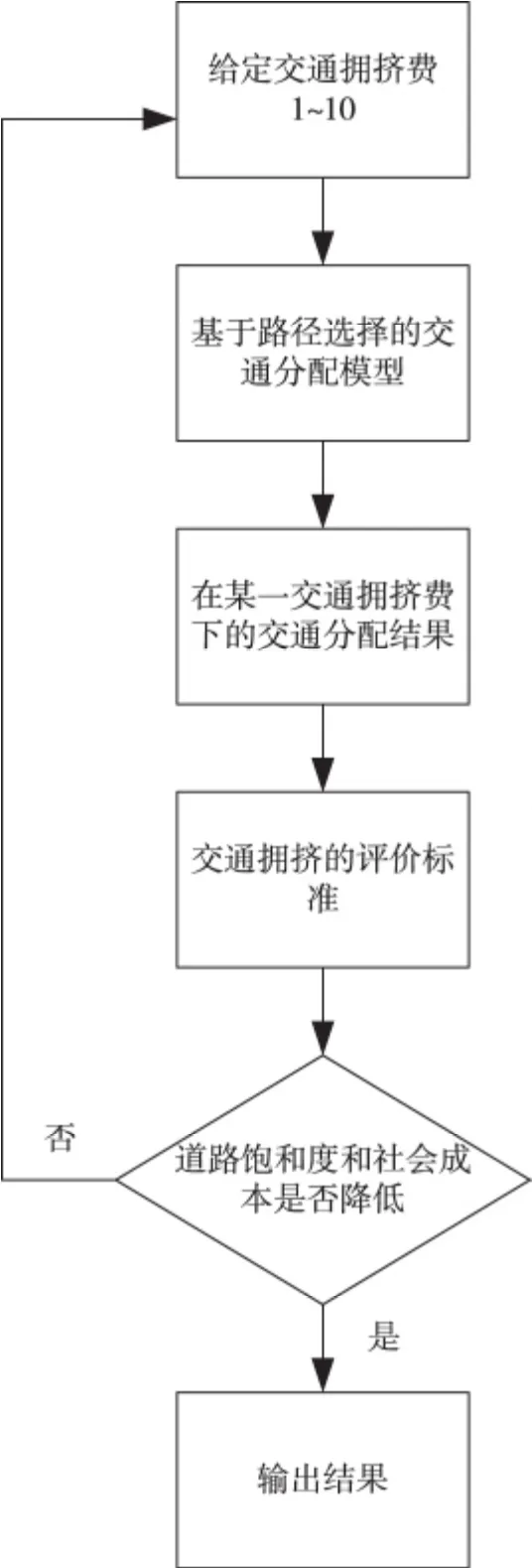
图1 基于路径选择的交通拥挤费定价模型

针对基于路径选择的交通流分配双层规划模型，可以通过将双层问题中的下层问题用它的Kuhn-Tucker［8］条件代替，转化为一个单层的参数线性互补问题。令为约束条件(6)对应的拉格朗日算子，那么拉格朗日函数为:

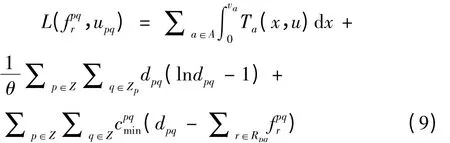
根据Kuhn-Tucker［8］条件，上述拉格朗日函数在极值点必须满足以下条件:

条件(12)可以简化为:

因此，在极值点处的双层规划模型可以转化为如下的单层问题，该单层问题可直接利用LINGO软件直接进行编程求解

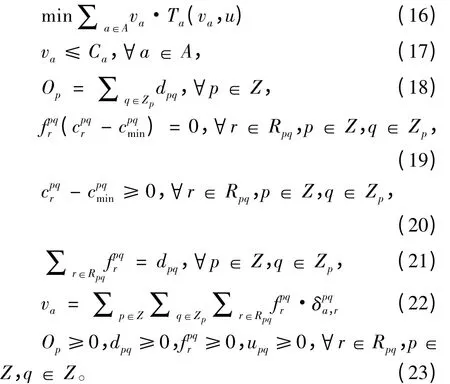
5 算例分析

考虑如图2 所示的道路网络，存在7 条路段和6 个结点。其中，结点1 和2 是起点，结点3 和4 是终点。网络中有4 对O -D 对分别为(1，3)，(1，4)，(2，3)和(2，4);有6 条路径分别为r1= {1}，r2= {2，5，6}，r3= {2，5，7}，r4= {4，5，6}，r5= {4，5，7}，r6= {3}。结点1 的出行需求O1= 90 ，结点2 的出行需求O2= 60。

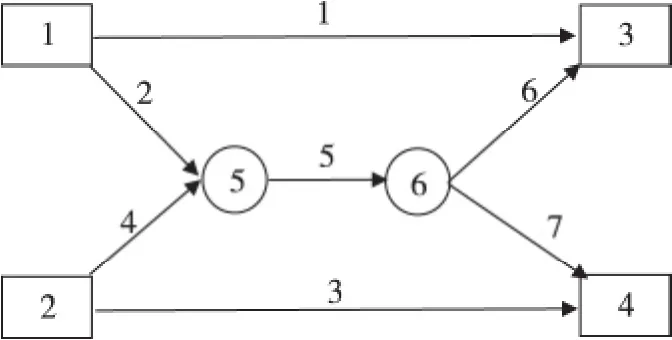
图2 算例网络

拥挤定价政策对出行者的影响可以理解为通过改变出行者广义费用Ta，从而改变其出行路径的过程。广义费用包括路段费用函数和拥挤费用，即

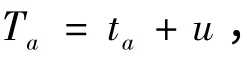
其中路段费用函数采用标准的BRP 函数形式，即

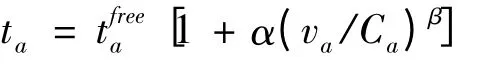
其中，参数取默认值为α = 0.15，β = 4 。道路属性参数的取值如表2 所示。

分别对路段1 收取1 ～10 元的拥挤费用，表3列出分别收取0 元、5 元和6 元交通拥挤费用，整个网络中路段流量情况。

表2 道路属性参数值

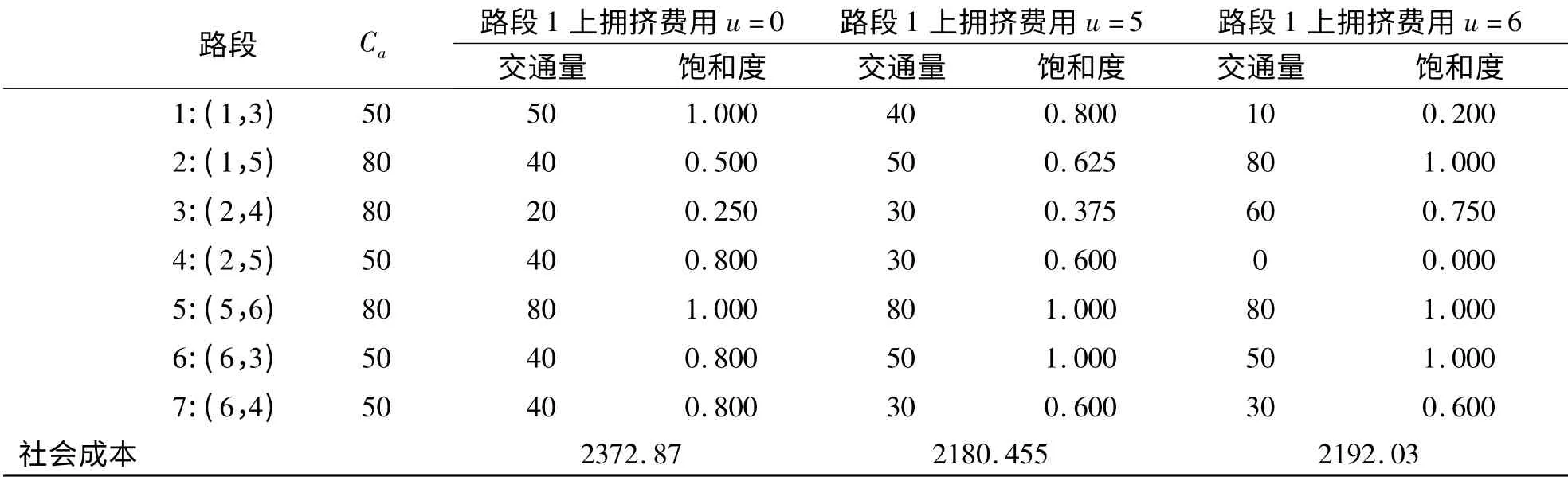
表3 不同拥挤费用时道路使用情况

观察表3，方案一有5 条拥挤路段，方案二有3条拥挤路段，而方案三有4 条拥挤道路。且社会成本也随着收取一定的拥挤费用有所下降又弹回。比较方案一和方案二，说明在相同的区域，当道路中形成拥挤时，当对拥挤道路收取拥挤费用，可有效缓解道路的拥挤情况，且降低社会成本。比较方案二和方案三，可知对拥挤道路收取拥挤费用不是越多越好，有可能反而造成道路分配的极端化，社会成本也会随之增加。

因此根据基于路径选择的交通拥挤费定价模型，此时我们选择的拥挤费是5 元，即u=5。

6 结语

收取拥挤费用是一项十分有效的交通需求管理措施，从广义上讲，交通拥挤是由于各种城市交通服务方式的价格低于成本引起的，尤其是城市机动车使用者仅仅支付其直接费用，而未支付其出行给社会和其他出行者带来的全部成本，从而鼓动了机动车交通量的迅速增长。本文考虑到用户与系统的需求，拥挤费的确定依赖于多路径选择下个人成本总量与社会总成本最优的多目标优化模型。交通拥挤收费除了可以抑制交通的不必要需求外，验证算例还表明，合理的交通拥挤收费可以较好地分配交通资源，促使交通网络达成更好的平衡。

［1］YANG H，LAM W H K. Optimal road tolls under conditions of queuing and congestion［J］. Transportation Researh A，1996，30:319 -332.

［2］YANG H，BELL M G H.Traffic restraint，road pricing and network equivibrium［J］.Transportation Research B，1997，31:303 -314.

［3］李志纯，谷强，史峰. 弹性需求下拥挤道路收费的模型与算法研究［J］.交通运输工程学报，2001，1(3):81 -85.

［4］郭瑞军，王晚香.城市交通拥挤的社会成本分析初探［J］，城市公共交通，2008(4):26 -29.

［5］吴中，何群.缓解交通拥挤的多目标优化模型和算法研究［J］.大连交通大学学报，2012，33(2):15 -19.

［6］陈来荣. 城市道路拥挤收费关键问题研究［D］. 北京:北京工业大学，2005.

［7］杜牧青.道路网络容量模型及算法［D］.南京:东南大学，2014.

［8］何瑞春.最优化理论及应用［M］.香港:香港GLOBAL-LINE 出版社，2007.