框架结构整体刚度对抗连续倒塌性能影响研究＊

宋志丹，曾明会，袁波*

( 贵州大学空间结构研究中心，贵州贵阳550003)

从1968 年英国伦敦Ronan Point 公寓因煤气泄漏而发生爆炸以来，经过40 多年的研究，抗连续倒塌方面已取得很大的进展，如英国建筑规程、欧洲规范、加拿大建筑规程等等。基于前人框架整体倒塌的基础上，如梁益［1］将楼板等效为相邻的框梁荷载，对按照我国规范设计的3 层混凝土框架进行了连续倒塌仿真，分析了它的倒塌能力，并对该框架进行抗连续倒塌设计;师燕超［2］应用有限元显示动力分析软件LS-DYNA 对爆炸荷载作用下2跨3 层框架结构进行倒塌分析，提出应该倒塌分析中考虑初始条件;李易［3］对非整体现浇楼板框架和整体现浇楼板框架的抗连续倒塌机制进行了分析，并考虑了抗震烈度因素等。本文为了简化分析模型，提出了一种静力简化方法来讨论整体刚度对抗连续倒塌承载力的影响。

1 模型建立

以一榀框架为例抗连续性倒塌分析方法主要是先去掉失效柱，然后在失效柱以上各层相邻的梁上竖向荷载乘以放大系数β［4］之后进行静力分析。

1.1 模型配筋设定

如图1 所示，本文选定的结构是一榀四跨五层框架，层高3.6 m，跨距为7.2 m，柱尺寸为500 mm×500 mm，梁尺寸为300 mm ×600 mm，梁上线荷载为Q kN/m(不包括梁的自重)，混凝土等级为C30，受力钢筋为HRB400，配筋结果见表1。

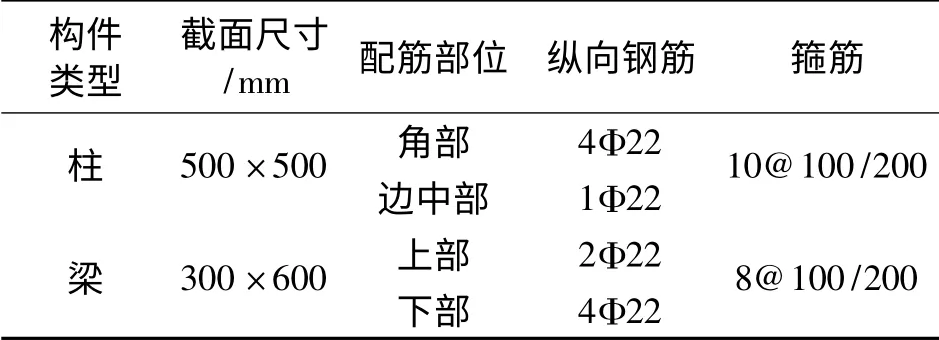
表1 模型配筋表

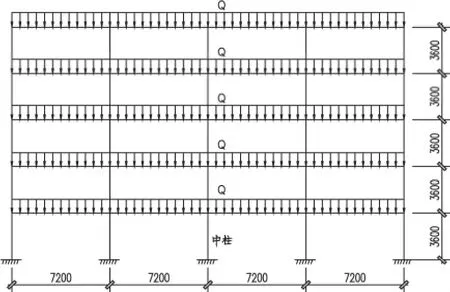
图1 模型结构图

1.2 Abaqus 的混凝土损伤模型

Abaqus 的混凝土损伤模型参数主要是基于Lubliner［5］et al.(1989)以及Lee、Fenves［6］(1998)来设定的。其主要理论内容如下:

(1)应变率分解

(2)应力-应变关系

1.3 有限元模型的建立以及分析参数的设定

应用有限元软件Abaqus，选择钢筋混凝土组合式模型［7］，分别定义钢筋和混凝土的本构关系，假定钢筋与混凝土粘结性能良好。混凝土选择梁单元，模型选择混凝土损伤模型，本构关系选择混凝土设计规范［8］中单轴压缩与单轴拉伸应力-应变曲线，不考虑损伤;Abaqus 中混凝土梁单元可以插入钢筋，所以利用关键字* rebar 把钢筋单元插入混凝土单元中组成钢筋混凝土组合式模型，这样可以保证混凝土与钢筋粘结性能良好，而钢筋本构关系［9］主要有理想弹塑性模型、双折线模型、强化模型等，而本文选择双折线弹塑性模型，如图2、3、4 所示，参数也是按照混凝土设计规范［8］数值进行设定。在分析中假定梁柱节点刚接。具体取值见表2、3、4。

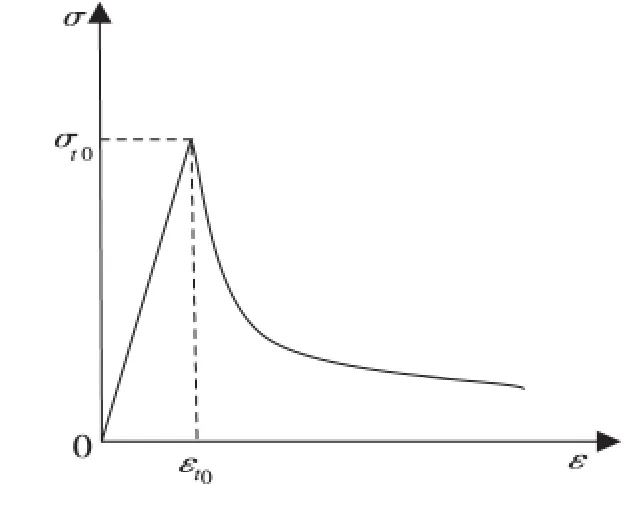
图2 混凝土单轴拉伸应力-应变曲线

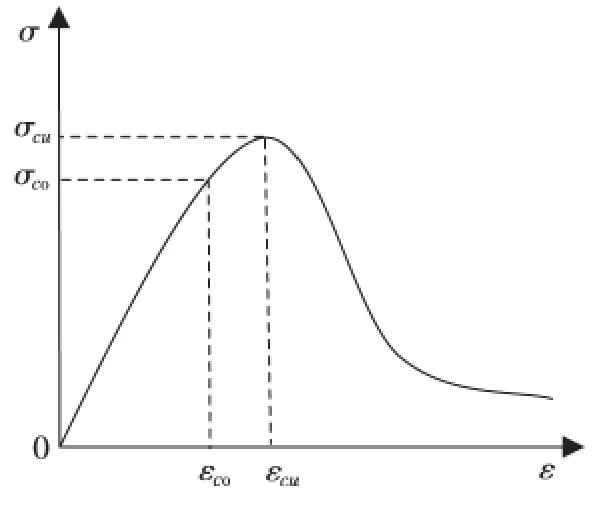
图3 混凝土力学参数

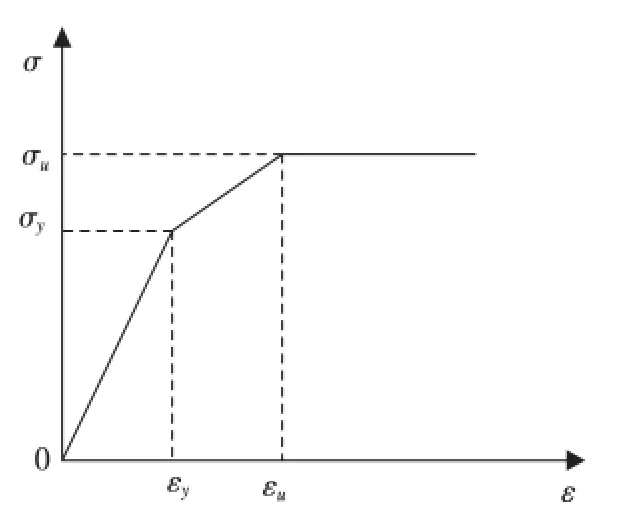
图4 钢筋本构关系曲线

表2 混凝土力学参数

表3 混凝土损伤模型参数

表4 钢筋力学参数表

2 方法的验证

2.1 刚度系数K1、K2、K3 参数的确定

建立两个一品框架结构有限元模型，并在结构中A、B 两点加上相应方向的集中力，如图5、6 所示。然后用有限元软件Abaqus 进行弹塑性推覆分析，选择收敛性较好的位移加载方式，得到力和位移之间的关系曲线，从曲线中可以看出，曲线最开始是一段直线，这是处于弹性阶段，当进入塑性阶段后，曲线显示出非线性，如图7 所示。曲线中力与位移的比值就是刚度系数K1、K2、K3(由于结构左右对称，K1=K2)，这里的刚度系数在弹性阶段是不变值，进入塑性之后随着位移的变化而变化。刚度系数K1、K2、K3可以用非线性弹簧Spring2 来模拟。

图5 K1、K2 刚度系数求解示意图

图6 K3 刚度系数求解示意图

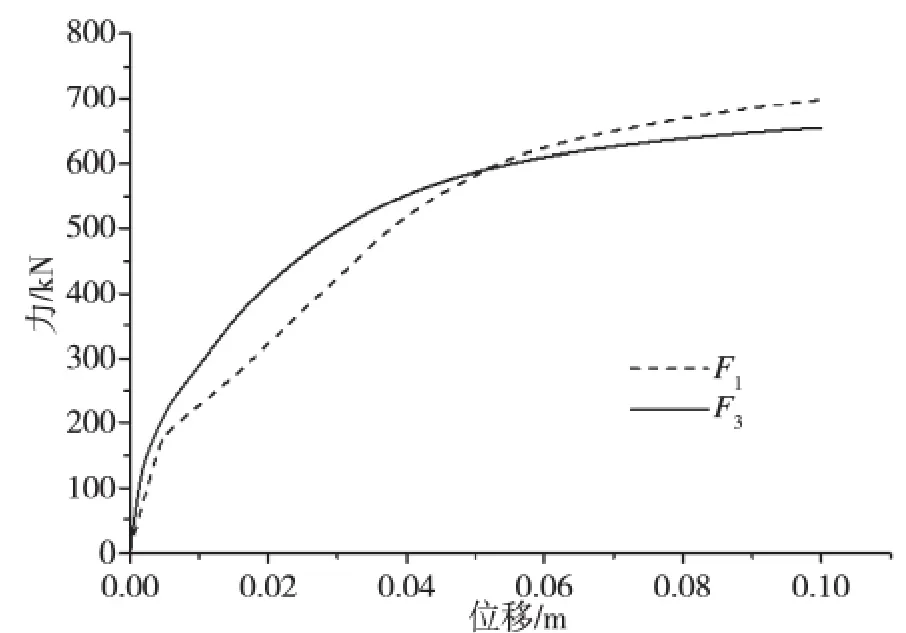
图7 F-位移关系曲线图

2.2 原模型与等效模型计算结果对比分析

应用Abaqus 的非线性弹簧功能等效刚度K1、K2、K3，在梁上线荷载Q=9 kN/m 的作用下进行竖向推覆分析，如图8、9 所示，分析步时间长度都为1，增量步由软件自动控制，得到两个模型的对比曲线图，如图10 所示。从图中可以看出，在相同的时间长度下，失效点的竖向位移基本相同，并且最终得到的曲线的变化趋势也是一样，原模型的最终位移为0.026838 m，而等效模型的最终位移为0.026890 m，两者相差0.2%不到，这说明等效模型是可行的。

2.3 两侧刚度K1、K2 对抗连续倒塌承载力的影响

图8 原模型推覆示意图

图9 等效模型推覆示意图

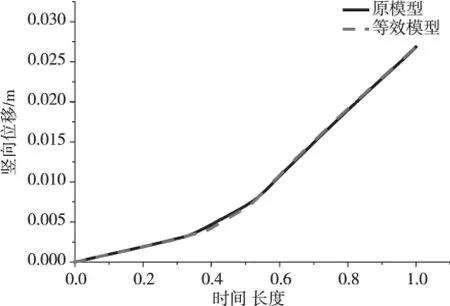
图10 两种模型竖向位移随时间长度变化对比曲线图

如图11 所示，假定结构左右对称，则K1=K2，在失效柱点加上集中力F，对等效模型在不同侧向刚度K1、K2下作推覆分析，假定两端弹簧处于线性阶段(K1、K2为定值)，分析步时间长度为1，加载方式为位移加载。经试算，当两侧刚度系数大约为108N/m 以上时，等效模型才到达极限荷载;而根据“强柱弱梁”［10］的抗震设计理念，梁要先于柱破坏，而当刚度系数小于108N/m 时，即使竖向位移趋近于无穷，等效模型始终达不到极限荷载，所以这种情况是不存在的。因此取K1= K2，均为108、109、1010、∞N/m(两端固定)来分析两侧刚度对抗连续倒塌承载力的影响。

图11 不同刚度系数K1、K2 下推覆分析加载示意图

如图12 所示，在不同刚度系数下，荷载曲线在最高点出现下降段，等效模型已达到极限荷载。等效模型在不同刚度系数下的极限荷载见表5，各个刚度系数下，极限荷载相差都在3%以内，这说明侧向刚度对抗连续倒塌承载力的影响很小［11］。

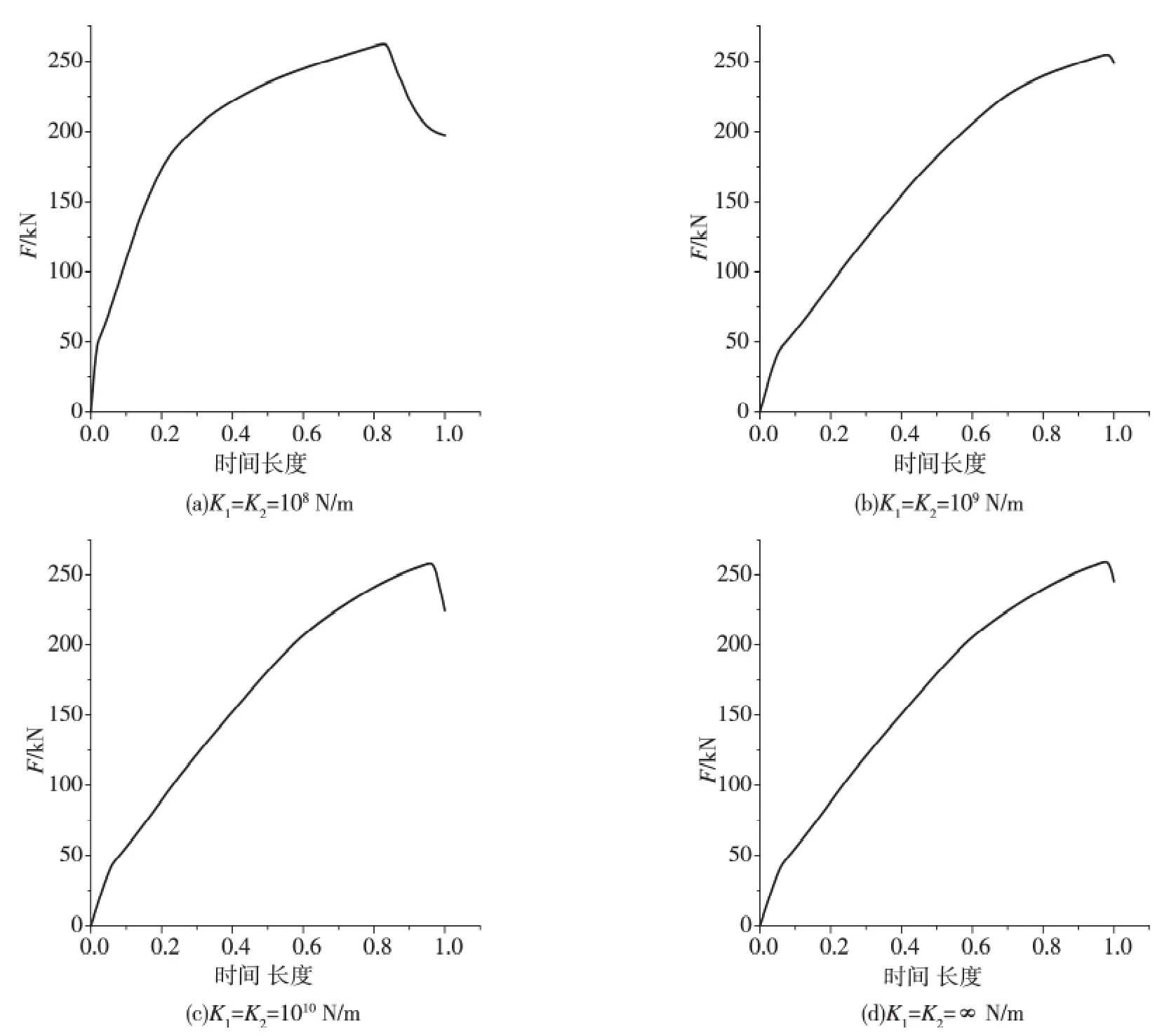
图12 不同侧向刚度系数K1、K2 下推覆曲线图

表5 不同侧向刚度下抗连续倒塌极限承载力表

2.4 刚度K3 对抗连续倒塌承载力的影响

如图13 所示，假定等效模型两端固定，在失效点加上集中力F，加载方式为位移加载，取刚度系数K3为103、106、109N/m 进行分析。图14 是不同刚度系数K3下该结构的推覆曲线(图中荷载F1是集中力F 扣除弹簧所承担的荷载所得)，从图中可以看出，不同刚度下推覆曲线基本重合，说明刚度系数K3对抗连续倒塌承载力基本无影响。

图13 不同刚度系数K3 下推覆分析加载示意图

3 结论

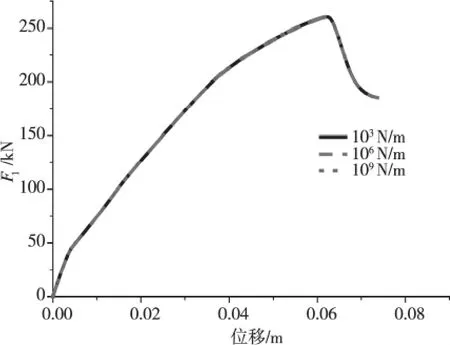
图14 不同刚度系数K3 下推覆曲线图

(1)将两个模型的竖向力与位移关系曲线进行对比，结果显示局部等效模型与整体模型结果吻合很好，说明局部等效模型是可行的;

(2)应用局部等效模型和软件Abaqus 分析了侧向刚度和失效柱点上层结构刚度的改变对失效点最大抗力的影响，结果显示随着侧向刚度的改变，最大抗力的差别都在3%以内，而随着上层结构刚度的改变，最大抗力基本无变化。这说明两侧刚度和上层结构刚度对最大抗力的影响很小，可以忽略。

［1］梁益，陆新征，李易.3 层RC 框架的抗连续倒塌设计［J］.解放军理工大学学报:自然科学版，2007，8(6):659 -664.

［2］师燕超，李忠献，郝洪. 爆炸荷载作用下钢筋混凝土框架结构的连续倒塌分析［J］. 解放军理工大学学报:自然科技版，2007，8(6):652 -658.

［3］李易，陆新征，叶列平. 钢筋混凝土框架抗连续倒塌机制研究［J］.建筑科学，2011，27(5):17 -19.

［4］Applied Research Associates，Inc. Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects［S］. Washington，D. C.:Prepared for the US General Services Administration，2009.

［5］Lubliner J，J Oliver，S Oller，et al. A Plastic-Damage Model for Concrete［J］.International Journal of Solids and Structures，1989，25(3):229 -326.

［6］Lee J，G L Fenves. Plastic-Damage Model for Cyclic Loading of Concrete Structures［J］. Journal of Engineering Mechnics，1998，124(8):892 -900.

［7］牟晓光，王清相，司炳君. 钢筋与混凝土粘结试验及有限元模拟［J］. 计算力学学报，2007，24(3):379 -384.

［8］中华人民共和国建设部. GB 50010 -2010，混凝土结构设计规程［S］. 北京:中国建筑工业出版社，2010.

［9］王传志，滕智明. 钢筋混凝土结构理论［C］.北京:中国建筑工业出版社，1985.

［10］中华人民共和国建设部. GB 50011 -2010，建筑抗震设计规范［S］. 北京:中国建筑工业出版社，2010.

［11］曾明会，袁波，李霞昭. 次梁对钢筋混凝土框架结构连续性倒塌动力效应的影响研究［J］. 贵州大学学报:自然科学版，2014，31(2):95 -99.