基于EverStressFE层间状态的匝道沥青路面结构三维有限元分析
2015-08-26张世洲
张世洲
基于EverStressFE层间状态的匝道沥青路面结构三维有限元分析
张世洲
(辽宁省交通规划设计院,辽宁 沈阳 110166)
采用专业沥青路面三维有限元分析程序EverStressFE,对典型匝道沥青路面结构在不同层间粘结状态下进行力学响应计算。结果表明沥青层间水平和竖向应变、路表弯沉及沥青层疲劳寿命受层间粘结状态变化最为敏感,无机结合料层受层间粘结影响相对较小。
道路工程;路面结构;层间状态;匝道;三维有限元分析;EverStressFE
目前,我国高速公路互通立交匝道路面结构大多采用无机结合料基层沥青路面结构,面层结构往往采用与主线相同的上面层和中面层,与主线面层结构相比少了下面层,某高速公路主线与互通立交匝道的路面典型结构如图1所示。沥青路面结构设计假定路面结构层间完全连续,即各层间粘结状态完好,没有产生相对滑动。而实际上由于各层材料在物理力学性质上的显著差异,在行车荷载、环境、气候等因素的影响下,道路通车运营后各层之间并未完全粘结,在层间剪应力的作用下出现相对滑动,处于不完全连续状态。国外有对柔性基层沥青路面的研究表明[1],层间相对滑动是造成路面结构损坏的重要因素,大大降低路面结构的整体使用性能;对于相对较薄的沥青面层路面结构,若层间粘结状态变差,将促使路面早期损坏,出现推挤、拥包等病害。本文针对我国典型匝道路面结构,采用专业沥青路面三维有限元分析程序EverStressFE[2],分别对路面结构层间处于完全粘结、部分粘结和完全滑动3个状态进行力学响应分析,以得出路面结构层间粘结状态对路面结构整体性能影响的规律。
1 计算模型与层间接触参数
1.1计算模型
采用现行公路沥青路面设计规范建议的双轮组单轴100 kN标准轴载(BZZ-100)计算参数,如表1所示。
模型建立以轮轴为Y方向,以车辆行驶前进方向为X方向,路面结构深度向下方向为Z方向。根据当量双圆均布荷载的对称关系,以Y方向和两轮中心面截取1 m×1 m的有限元模型,如图2所示。模型边界条件水平和向下均为无限延伸的自由端,有限元模型网格划分共4 180个单元,20 349个节点,如图3所示。选取典型匝道路面结构物理力学性质参数如表2所示。
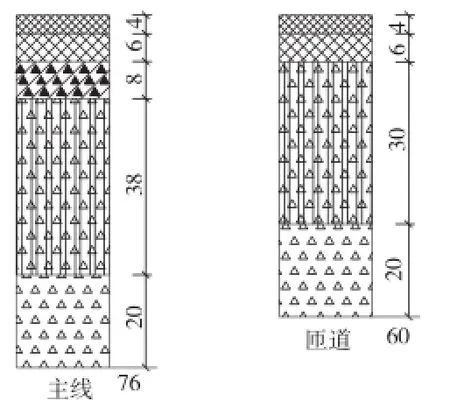
图1 高速公路典型沥青路面结构图(单位:cm)

表1 标准轴载计算参数

图2 模型建立
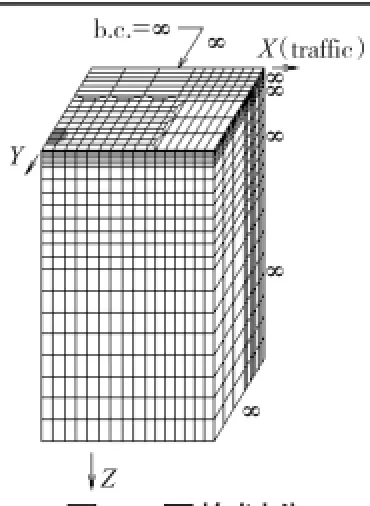
图3 网格划分

表2 标准轴载计算参数
1.2层间粘结状态参数
EverStressFE程序引入剪切反应模量Ks来表征层间的粘结状态,用层间剪应力与层间相对水平位移的比值来表示。Ks值越大,说明层间粘结状态越好,越趋于完全连接状态;Ks值越小,说明层间粘结状态越差,越趋于相对滑动状态。有研究表明[1-3],当Ks≤0.01 MPa/mm时,即可认为层间处于完全光滑状态;当0.01 MPa/mm<Ks<100 MPa/mm时,可认为层间处于完全光滑与完全连续状态之间,即处于部分连续状态;当Ks≥100 MPa/mm时,即可认为层间处于完全连续状态。
2 层间不同粘结状态下的路面力学响应分析
本文选取Ks=0完全光滑状态、Ks=∞完全连续状态、Ks=50 MPa/mm部分粘结状态、Ks=20 MPa/mm部分粘结状态,分别计算路面结构各层应变、弯沉等力学响应指标。
2.1层间粘结状态对水平应变的影响
以轮载轴向所在的平面来分析各层间应变分布情况,Y-Z面上各层水平应变的梯度变化如图4所示。
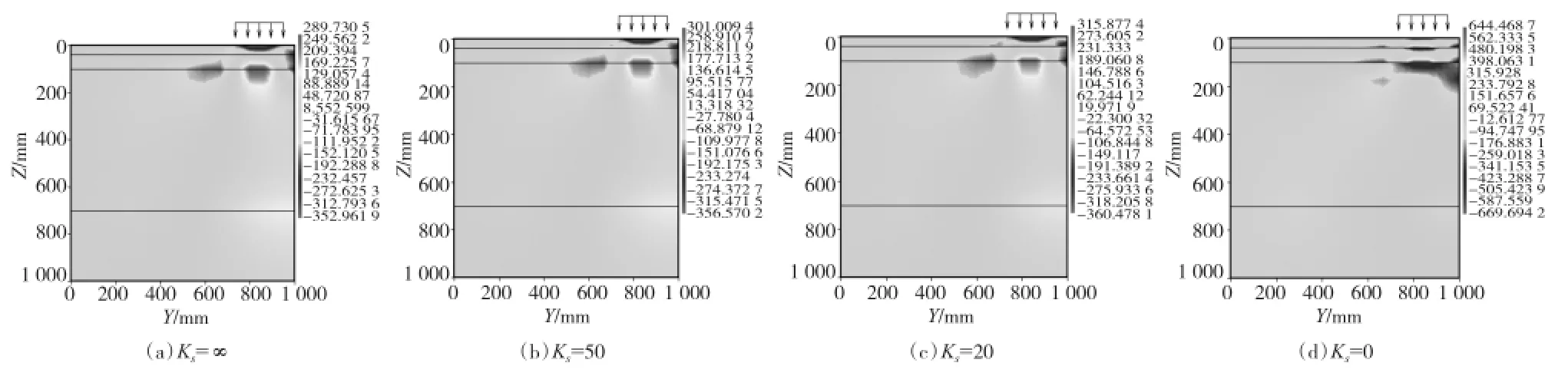
图4 Y-Z面上各层水平应变云图
由图4可以看出,当Ks由∞→50 MPa/mm→20 MPa/mm→0,即层间状态由完全粘结→部分粘结→完全光滑的变化过程中,沿轮载边缘向下应力扩散角附近存在一定范围的压应变,下面层底部、底基层底部均为拉应变,上面层底部处于完全粘结状态时为压应变,处于部分粘结、完全光滑状态时均为拉应变。层间处于完全光滑时,由于应力重分布,各层间出现完全不同的水平应变状态,应变等值包络线不再连续,明显看出上面层底部和下面层顶部分别处于受拉和受压两种不同的状态,下面层底部和基层顶部分别处于受拉和受压状态。各层均在轮载中心正下方达到应变最大值,层间处于不同粘结状态时各层底部最大应变值如表3所示。从表3可以看出各层底部水平应变峰值随着层间完全粘结至完全光滑的过程中均有增加,上面层底部处于完全光滑状态(Ks=0)时水平拉应变相比部分粘结状态(Ks=50 MPa/ mm)增加3 696.92%,部分粘结状态随着Ks的减小也增加较大,Ks=20 MPa/mm时的上面层底部水平拉应变相比Ks=50 MPa/mm增加235.03%,说明上面层底部水平应变受层间粘结状态的状况较为敏感,层间粘结越好上面层越不容易开裂,否则极易引起路面的损坏。下面层底部处于部分粘结状态时水平拉应变增加不大,较完全粘结状态(Ks=∞)分别增加3.46%(Ks=50 MPa/mm)和8.45%(Ks=20 MPa/mm),但完全光滑状态(Ks=0)下面层底部增加较大,为完全粘结状态时的119.54%。同样可看出,底基层底部处于部分粘结状态时水平拉应变增加不大,较完全粘结状态(Ks=∞)分别增加2.08%(Ks=50 MPa/mm)和3.03%(Ks=20 MPa/mm),但完全光滑状态(Ks=0)下面层底部增加较大,为完全粘结状态时的46.29%。可以看出,各层底部水平应变均随着层间由粘结变为光滑而增大,上面层底部水平应变对层间粘结状态最为敏感、成倍增加,下面层和底基层底部水平应变增幅逐渐降低。
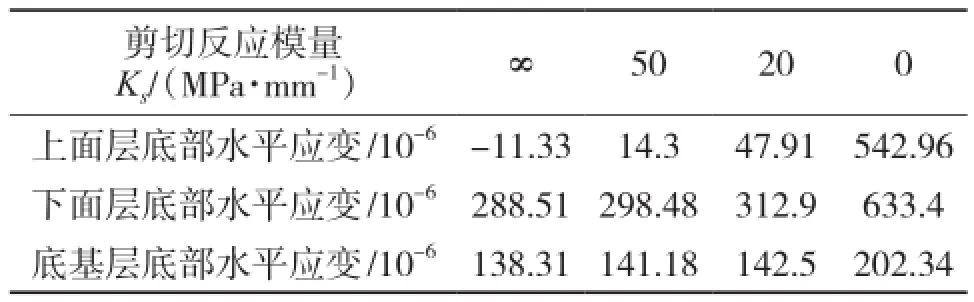
表3 不同粘结状态时各层底部水平最大应变
2.2层间粘结状态对竖向应变的影响
Y-Z面上各层水平应变的梯度变化如图5所示,由图5可以看出,当Ks由∞→50 MPa/mm→20 MPa/mm→0,即层间状态由完全粘结→部分粘结→完全光滑的变化过程中,各层均在轮载中心正下方达到应变最大值。层间处于完全光滑时,由于应力重分布,各层间出现完全不同的竖向应变状态,应变等值包络线不再连续,出现明显的随层分布,下面层顶部和土基顶部竖向应变相比完全粘结和部分粘结状态均有不同程度的减小,而基层顶部竖向应变却有大幅度的增加。层间处于不同粘结状态时各层顶部最大竖向应变值如表4所示。从表4可以看出各层顶部竖向应变随着层间完全粘结至部分粘结的过程中均有增加,但增加幅度均不是很大,下面层顶部处于部分粘结状态(Ks=50 MPa/mm、Ks=20 MPa/mm)时竖向压应变分别比完全粘结状态(Ks=∞)增加0.27%和1.34%;基层顶部竖向压应变分别增加0.45%和4.22%;土基顶部竖向压应变分别增加11.94%和29.20%。说明在层间状态由完全粘结至部分粘结的过程中,各层顶部竖向压应变具有增大的趋势,下面层、基层、土基顶部竖向压应变受层间状态影响的敏感程度依次增大。当层间处于完全光滑时应力重分布,从表4可以看出,下面层、土基顶部竖向压应变均有减小,比完全粘结状态分别减小98.1%和13.3%;而基层顶部竖向压应变却增加87.0%。说明层间处于完全滑动状态时,各层应力重分布,下面层和基层顶部竖向压应变较为敏感,比完全粘结状态时分别出现大幅减小和增加;土基顶部竖向压应变相比减小的幅度不大。
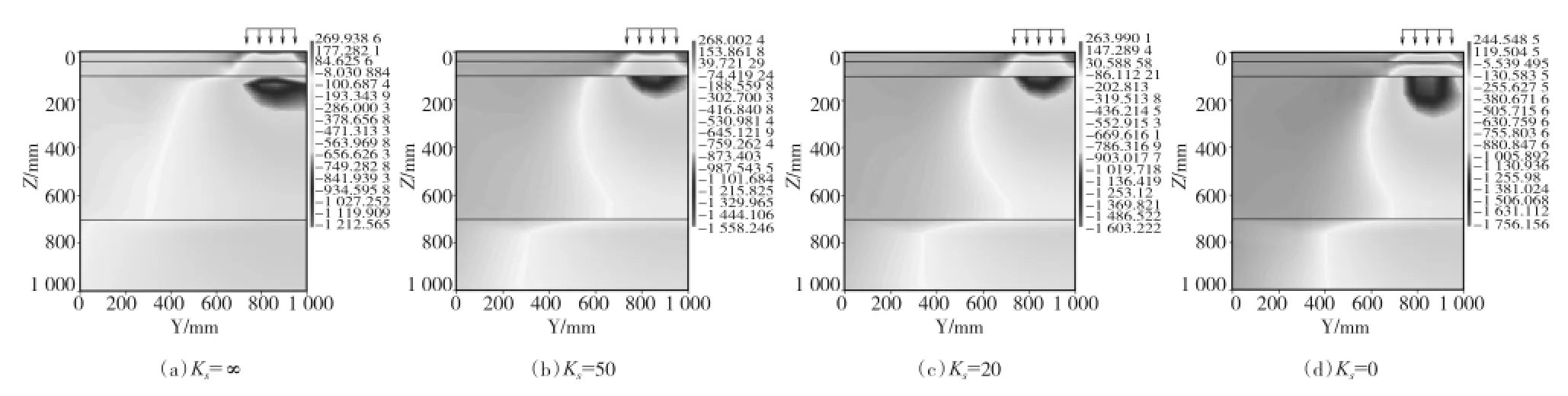
图5 Y-Z面上各层竖向应变云图

表4 不同粘结状态时各层顶部竖向最大应变
2.3层间粘结状态对弯沉的影响
Y-Z面上弯沉的梯度变化如图6所示。可以看出当Ks由∞→50 MPa/mm→20 MPa/mm→0,即层间状态由完全粘结→部分粘结→完全光滑的变化过程中,各层均在轮载中心正下方达到弯沉最大值,弯沉沿路面结构深度向下依次减小,路表面弯沉值最大。弯沉峰值随着层间完全粘结至部分粘结的过程中均有增加,但增加幅度均不是很大,部分粘结状态(Ks=50 MPa/mm、Ks=20 MPa/mm)时弯沉峰值分别比完全粘结状态(Ks=∞)增加1.05%和2.28%;当层间处于完全光滑时弯沉峰值增加43.91%,说明层间处于完全滑动状态时,弯沉峰值变化幅度较大,此时路面使用性能将大大降低,极易出现车辙现象。

图6 Y-Z面上各层弯沉云图
3 层间粘结状态对路面结构使用性能的影响
按照沥青路面结构设计方法的研究报告,沥青层疲劳寿命预估模型如下:
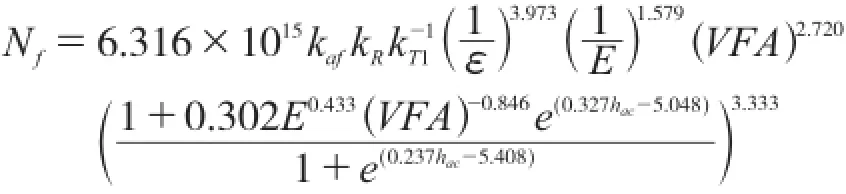
无机结合料层的疲劳寿命预估模型如下:

模型中各参数意义及取值可参见《公路沥青路面设计规范》(征求意见稿)[4]和《基于多指标的沥青路面结构设计方法研究》[5]。按照建议的基准3层沥青路面结构,将表3的计算结果代入以上沥青层和无机结合料层的疲劳寿命预估模型,可得到层间不同粘结状态下沥青层和无机结合料层疲劳寿命计算结果,如表5所示。由于层间处于完全粘结状态时(Ks=∞),上面层底部为压应变,处于受压状态,因此对该状态下的沥青层疲劳寿命不予计算。由表5可知,层间状态由完全粘结→部分粘结→完全光滑的变化过程中,沥青层疲劳寿命急剧下降,呈几何级数递减,当层间状态处于完全光滑时,疲劳寿命计算结果为1.123次,说明沥青层完全疲劳开裂,已几乎不能再承受车辆荷载,计算结果与实际较为吻合;而无机结合料层疲劳寿命也有显著降低,但数量级上无变化,说明无机结合料层疲劳寿命受层间粘结状态影响较小,即使在沥青层间粘结完全失效的情况下,无机结合料层仍能在设计的标准轴载车辆作用下正常使用。

表5 不同粘结状态时沥青层和无机结合料疲劳寿命
4 匝道纵坡对层间粘结状态的影响
高速公路互通立交匝道相对主线具有较大的纵坡,且匝道路面窄、转弯急,易造成车辆频繁的加减速行驶,会产生沿匝道坡面较大的行车荷载分力,匝道纵坡越大产生的坡面分力也就越大。有研究表明[8]随着坡面分力的增大,匝道路面面层层底应力随之增大,对上面层的影响最为明显。进而影响各层间粘结状态,造成匝道沥青路面的层间推挤滑移破坏,降低路面结构的使用性能。
5 结论
本文采用专业沥青路面三维有限元分析程序EverStressFE对典型匝道路面结构进行计算,分析不同层间粘结状态下沥青路面结构的力学响应,主要结论如下:
(1)剪切反应模量能够定量表征层间的粘结状态。其值越大,说明层间粘结越好,越趋于完全连续状态;其值越小,说明层间粘结越差,越趋于滑动状态。
(2)随着层间状态由完全粘结→部分粘结→完全光滑的变化过程中,路面结构各层底部水平拉应变均有增大的趋势,沥青层间水平应变对粘结状态最为敏感、成倍增加,面层与基层和底基层与土基的层间水平应变增幅逐渐降低。
(3)随着层间状态由完全粘结至部分粘结的过程中,各层顶部竖向压应变具有增大的趋势,下面层、基层、土基顶部竖向压应变受层间状态影响的敏感程度依次增大。当层间处于完全滑动状态时,下面层和基层顶部竖向压应变较为敏感,相比完全粘结状态时分别出现大幅减小和增加的现象;土基顶部竖向压应变相比减小的幅度不大。
(4)弯沉峰值随着层间完全粘结至部分粘结的过程中均有增加,但增加幅度均不是很大。当层间处于完全光滑时,弯沉峰值变化幅度较大,此时路面使用性能将大大降低,极易出现车辙倾向。
(5)随着层间状态由完全粘结至部分粘结的过程中,沥青层和无机结合料层的疲劳寿命均呈下降趋势,沥青层较为敏感急剧下降,当层间状态处于完全光滑时,沥青层疲劳使用寿命达到极限,需进行路
面重新罩面或补强。而无机结合料层疲劳寿命受层间粘结状态影响较小,即使沥青层间粘结完全失效的情况下,无机结合料层仍能在设计的标准轴载车辆作用下正常使用。
(6)本文选取典型匝道沥青路面结构进行的沥青层和无机料结合层疲劳寿命分析,与已有高速公路主线典型结构研究[7-8]相比均较低,与主线承担主要交通量而匝道分流交通量的实际情况较为吻合。
[1]Al Hakim B. An improved backcalculation method to predict flexible pavement layers moduli and bonding condition between wearing course and base course[D]. Liverpool:Liverpool John Moores University,1997.
[2]The Washington State Department of Transportation. EverStress FE1.0 software for 3D Finite Element Analysis of Flexible Pavement Structures[M]. 2009.
[3]Muslich Hartadi Sutanto,ST,MT. Assessment of bond between asphalt layers[D]. Nottingham:The University of Nottingham,2009.
[4]JTG D50—2006公路沥青路面设计规范[S].
[5]中交路桥技术有限公司.基于多指标的沥青路面结构设计方法研究[R]. 2012.
[6]肖鑫. 沥青路面下坡路段层间剪应力的分析[J].北方交通,2011(9):1-3.
[7]崔学民,陈德华. 超载作用下沥青混凝土路面的受力特性分析[J]. 公路,2012, (2):52-55.
[8]张久鹏,武书华,裴建中,等.基于剪切弹性柔量的基-面层间接触状态及路面力学响应分析[J]. 公路交通科技,2013(1):6-11.
3D Finite-element Analysis of Asphalt Concrete Pavement Structure Based on EverStressFE Bond Condition between Adjacent Layers
Zhang Shizhou
(Liaoning Provincial Communication Planning &Design Institute, Shenyang 110166, China)
Using professional asphalt pavement 3D finite-element analysis program EverStressFE, mechanical responses under different bond condition between adjacent layers for typical asphalt concrete pavement structure of highway interchange ramps are calculated. The results show that horizontal strain, vertical strain, deflection and fatigue life are most sensitive to the bond condition between adjacent asphalt layers, comparatively less sensitive to the bond condition between inorganic combined material layers.
road engineering; pavement structure; bond condition between adjacent layers; ramp; 3D FEA; EverStressFE
U416.217
A
1672-9889(2015)06-0001-04
张世洲(1980-),男,黑龙江桦川人,工程师,主要从事道路工程设计工作。
(2014-06-09)
