试谈中学有效数学课堂非预设生成

福州第二十四中学 陈丽英

试谈中学有效数学课堂非预设生成

福州第二十四中学 陈丽英

当前，为保教学质量而以考定教、重复机械式的、填鸭式的教学现象依然存在，使喜欢数学的学生越来越少。该文结合教学实践，通过数学知识观念、数学思想的传授，把众多学生牢牢吸引住，给学生留下长久的思想激荡和对知识的深刻理解，从中感受到学数学的快乐。

中学数学 有效教学 自主建构

数学课堂效率的高低，不取决于教师打算教给学生什么，而取决于学生实际获得了什么。检验学生学习成果的关键在于教学近期目标与远期目标的有机结合，这应该是持续、恒动的一个过程。试想，一个孩童在没有触及数学之前，有可能还对数学持有一份矜持和向往，可是，如果经由近十年数学课的历练，不时淹没于无边无际的题海之中，受尽挫折，饱尝困惑，也许最终取得了高分，但其内心深处一定谈“数”色变，怯弱数学，害怕数学，最不愿做的试卷可能就是数学。这样的数学教学，只长成绩，不长快乐，称不上“加法”教学，却是地地道道的“减法”教学。如果有一种方法，能使我们的孩子不再为数学解题感到困乏无术、枯燥无味，而是真心实意地喜欢上数学课和数学解题，并能在课堂上和解题中体悟数学思维的魅力，进而迸发灵感的火花，品味学习的快乐，分享成长的幸福，那才是有效的数学教学。

教学生成，包括预设的生成与非预设生成。预设即预测与设计，是教师在课前对课堂内容进行清晰、理性的设想与安排，通过充分的教学预设与认真的功课准备，以期达到预期的教学效果；非预设生成，指的是师生教学活动离开或超越了原有既定的思路和教案，学生获得了非预期的发展，是教师个性化的教与学生个性化的学的重要体现。下面，试就“未曾预设，也见精彩”，谈谈对有效教学的粗浅理解。

课堂教学往往不可能完全按预定的轨道运行，要及时针对教学实际进行灵活调整与布控，促进有效生成，教师要关注课堂生成的新情境、新内容、新方法，更多关注学生在课堂中个性化的活动，留给学生自主想象和自主建构的空间。

1　捕捉学生思维亮点，融合智慧生成

要努力构建一种开放、和谐、愉快的教学环境，激起学生探究的热情，让学生能畅所欲言，充分暴露思维过程，引导学生大胆探索，留给学生一定的自主探索空间。

八年级下册学习平行四边形时，有这道例题：

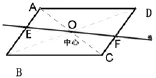
例题：如图，平行四边形对角线AC、BD相交于点O，EF过O与AC、BD分别交于点E、F. 求证：OE=OF。

例题引申一：如图，过中心

O的一直线与平行四边形对边分

别相交于E、F. 求证：OE=OF。

例题引申二∶你能画一条直线把该平行四边形的面积两等分吗？看谁的办法多。

例题引申三：如图，你能画一条直线把该图的面积两等分吗？看谁的办法多？

学生有如下三种解答：

学生 1（突发奇想）：还有没有其他的画法呢？符合题目的直线就只有三条吗？

教师：你提出的问题说出了大家的心声与愿望，有谁可以回答这个问题呢？大家都学习过图形变换的知识哦。

学生马上动手，气氛顿时活跃起来。

学生2（灵机一动）：如图，把直线a对应线段PN中点O旋转，使直线a仍与AF，BC相交。由于 POQΔ≌ NOMΔ，使得直线QM平分图形面积。（真是太好了！）

学生3（兴奋的补充）：由于A、F之间可以有无数个点，由直线a绕点O就可以得到无数条直线，那直线b、直线c也可以同样旋转，能平分图形面积的直线有无数条。

教师：看来这个问题有了完美的结局。

可是有一学生提问：直线a、b、c会不会都交于同一点呢？教师（兴奋的补充）：同学们试着画一下，三条直线有没有交于点O？

小组合作交流讨论，几何画板验证，得出：直线a、b、c都交于同一点G。

教师指导：点G就是图形的重心。阅读课本（人教版八年级下册）第123页 “课题学习：重心”。

教师：课后可以结合模型悬挂法找不规则图形的重心。

整整一节课，只解决这么一个问题，何况打乱了原定的教学计划，确实有些遗憾，可仔细一想，其意义又何止于解决了这一问题！让学生在动脑、动口、动手的活动中获取知识，发展智力，培养能力，促进了主动探索，积极思考，大胆猜想，把问题不断导向纵深。

2　自主探索，挖掘动态资源

课堂教学，不是课前设计和教案的展示过程，而是不断思考、不断调节、不断更新的生成过程，也是师生富有个性化的创造过程，一些无法预见的、从未经历的教学情境对我们是一种强大的激励与挑战。因此，在教学中要保持一种与学生共同学习、探索的心态，并与学生共同体验创新思维所带来的愉悦。下面这道题是中考复习中典型的例题：

在右图中，H是正方形ANQM的边 MQ上任意一点（与M，Q不重合），以HQ为一边向外作正方形 HQPB，问：NH与PM有怎样的关系？

常规解题：添加辅助线，延长NH交MP于点C。

突然一个学生说：我不需添加辅助线，而用旋转的观点看，相当简单，妙！△MQP可由△NQH绕点Q顺时针旋转90°而得，所以PM是由NH绕点Q顺时针旋转90°而得，所以NH与PM垂直且相等。

他的巧思妙想打动了我和其他学生：几何题图形中的几何性质比较隐晦，条件分散，题设与结论间某些元素的互相关系在所给的图形中不易发现，难以下笔而感到束手无策，如果我们应用运动观，利用翻折、旋转、平移等全等变换将那些分散、远离的条件从图形的某一部分转移到适当的新的位置上，使题设和结论中的元素之间的联系更加明显，由分散变为集中，使“辅助线”的思考更加集中而自然，相互间的关系变得清晰了，从而能将求解的问题灵活转化，变难为易，同时也使解题更为有趣。

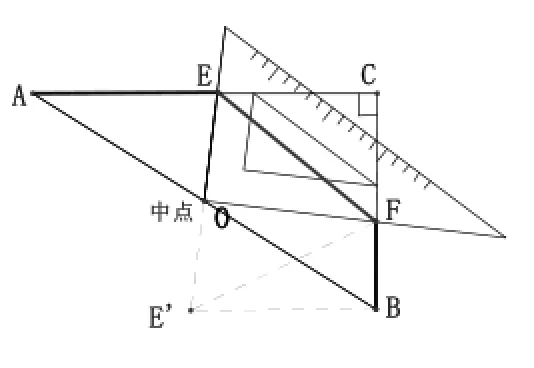
在这种情况下，我顺着学生的思路改变了原定计划，而临时利用手边直角三角板给学生出题：如图，将一副三角尺按如图旋转，探索AE、EF、FB这三条线段能否组成一个以EF为斜边的直角三角形？

很快地，同学们就解出来了！

可是，突然有一学生问：若△ABC不是等腰三角形，而仅仅是直角三角形，上述结论还成立吗？

教师利用几何画板动态演示，学生共同探讨，得出：将三角形AOE绕点O旋转180°到△BOE’处，由于是全等变换，故有△AOE△BOE′，△BFE′是以FE′为斜边是直角三角形，问题得以解决。

最后师生一起总结：利用图形的全等变换是添辅助线的有效方法，它不仅可以使分散的条件相对集中起来，为题设和结论架起桥梁，可打破常规思路解题的思维局限，会获得意想不到的效果。

事实上，这节课在毫不预防的情境中，我为了不中断学生的思路，调整原先的教学设计，利用几何画板挖掘动态资源，收到意想不到的教学效果。

3　化逆境为顺境，将课堂引向精彩

当课堂出现超出预设，出现突发情况，置教师于尴尬境地时，教师要因地制宜根据出现的新情况，用以“急中生智”积累正能量，调整原先既定的教学思路和设想，化逆境为顺境，使教学活动贴近学生，将课堂引向精彩。下面结合笔者亲身经历的的一次课堂教学，谈点感受。

人教版七年级下册第六章《平面直角坐标系》，在第一节课《有序数对》的设计时，结合笔者自身的教学风格、教学目的以及学生的学情，对教材进行系统性的消化、融合，裁剪修改，做如下设计：

老师：今天我要找一位同学帮忙，请同学们帮我找出这位同学，我知道他坐在教室的第3列。（创设问题情境）

学生甲：第3排有8位同学，无法确定。

老师：看来一个数无法确定这位同学的位置，我想起来了，这位同学在第3列第5排，同学们再找找看。

学生乙：老师还是无法确定，前后边从哪边开始是第一排，左右边从哪边开始是第一列。

老师：看来我们要先规定一下方向，指定从门口起为第一列，第一排。第3列第5排的这位同学找到了吗？（老师板书画出规定正方向的横轴、纵轴）

大家齐声：“是他！”。我高兴地握住这位同学的手说，我们终于找到你了！

老师总结：看来我们准确找到一位同学的位置，需要知道两个有序的数对，第3列第5排，按从门口起第一列、第一排规定，将教室的座位画在黑板上（如下图），刚才这位同学的位置可用点坐标“（3，5）”表示，现在请在座的每位同学确定自己的位置，并用点坐标方法表示。

教室座位平面图

同学们很开心地数着自己的列数和排数，很快都准确地将自己的位置表示出来了，可是，突然有个学生从我后面的讲台右侧站起来说：“老师，我找不到我的位置！”此时，我咯噔了一下，糟了，这怎么还藏着一个……？（原来，前一节课上，他因为违反纪律，班主任临时将他调至这个位置了）我连忙说，不好意思，老师没看到你坐在这。更糟的是，正好有一位同学迟到了，他不好意思地站在门口，学生丙发问：老师能表示他的位置吗？我心里想，真是“祸不单行”啊，人算不如天算，这下该怎么圆场呢？

突然，我灵机一动，果断的决定在这里直接引入负数坐标来表示点，改变了教学原定计划，负数的引入和应用本来就是初一新生学习的一个大难点了，在这里恰巧得到自然而然的过渡和解决，而且能轻松地将两节课的内容出乎意料地融合在一节课完成（事实上，课后作业反馈学生掌握得很好）！

我兴奋地说：同学们，能帮帮这两位同学找到他们的位置吗？能用有序数对表示该两位同学的座位吗？经过同学们的讨论，最终得到教室座位表，得到了平面直角坐标系的有关知识。

要为学生创造宽松、民主、和谐的课堂氛围，把学习的主动权交还给学生，让学生自己去尝试、发现，去拓展、探索，去反思、推导，亲身参与思维活动，经历知识的建构过程，必须转变教学观念，创造性地使用教材，创造性地设计学习活动，在遇到非预设的情况时，应以灵活选择、有机整合、机智生成新的教学方案，使教学课堂更加精彩而有效。

作为一名中学数学教育者，我谨记：不能让学生因为我的数学课而讨厌数学，远离数学！我希望，他们喜欢数学课，在课堂上能真切感悟数学魅力，迸发数学思维的灵感，品味着学习的快乐，分享着成长的幸福。