巧妙搭“桥” 化动为静——关于2013年泉州市中考数学试题解答的商榷

◎福建省南安市金光中学 方明华

巧妙搭“桥” 化动为静
——关于2013年泉州市中考数学试题解答的商榷

◎福建省南安市金光中学 方明华

动态几何题题型新颖，既考查了多个知识点，又考查了多种运用数学思想的能力，试题综合性强.这就要求考生能够严密细致地观察问题，理清解答思路，采用构造法“搭桥引路，化动为静”，充分利用已知的条件去推导问题和解决问题。

中考数学；动态几何题；构造法；答案修正

动态几何题题型新颖，在考查中往往能呈现出较高的区分度，因此成为中考命题中的重要题型，也受到中学师生的高度关注.这种题型所考查的往往是多个知识点，同时考查多种运用数学思想的能力，涉及的知识面广，试题综合性强.所以在解答这一类的动态几何题时，要求考生能够严密细致地从多个角度观察问题，充分利用已知的条件分析问题，十分严谨地推导和解决问题，才能正确完整地写出答案.现以2013年泉州市中考数学试题的第25题为例，谈谈这个方面的一些见解.

一、理清思路，周密解答

（1）求∠ABC的大小；

（2）求点 P 的坐标，使∠APO=30°；

（3）在坐标平面内，平移直线BC，试探索：当BC在不同位置时，使∠APO=30°的点P的个数是否保持不变？若不变，指出点P的个数有几个？若改变，指出点P的个数情况，并简要说明理由．

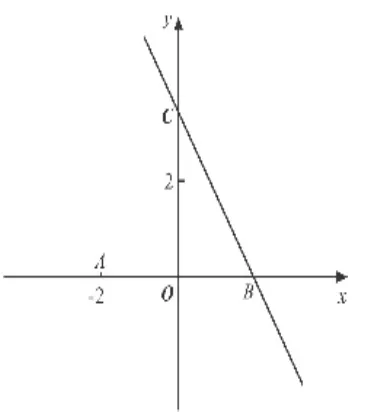
本题的命题立意是，以平面坐标为依托，考查几何、代数的相关知识点及数学方法的运用。其考查的知识与能力的范围横跨整个初中学段，知识覆盖面宽，方法包容性强，拓展辐射作用大.据统计，考生在这一题的平均得分为5.6分，获得10分以上高分的人数很少。如何在解题中做到深入细致地观察问题与推导问题，从而正确完整地解答问题，以下是具体的分析解答步骤.

步骤一，第（1）小题求∠ABC大小.

本小题考查的是关于“方程与一次函数的关系”这一知识点的掌握运用情况，其解答思路是先观察角的位置，在此基础上运用三角形的方法解决问题，这里需要运用直角三角形或特殊三角形的方法.

连接 AC（如图二示），由 A、B两点的坐标可知，它们关于y轴对称，由对称性质得AC＝BC，再运用勾股定理求得AC＝BC＝4，由此判断△ABC为等边三角形，可得∠ABC=600，并为解答第（2）小题作铺垫．

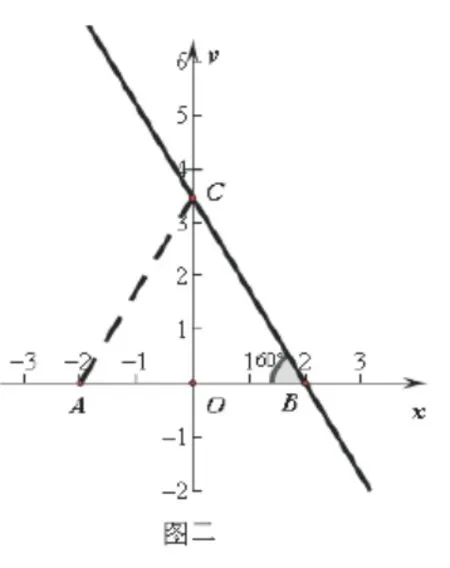
步骤二，第（2）小题求点P的坐标，条件使∠APO=300．

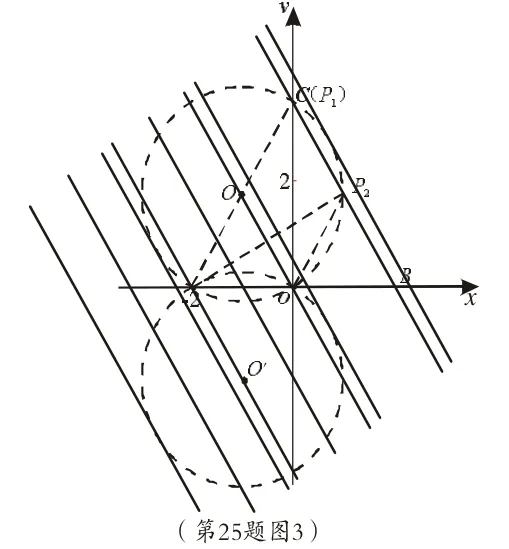
首先观察∠AOC的度数，利用“在圆中，直径所对圆周角为直角”这一知识点，得出A、O、C三点共圆，因此通过构造圆搭“桥”引路（如图三示），得出弦AO所对圆心角为600，这就把解决本问题转化为以AC为直径的圆与直线BC的公共点问题，即直线与圆的位置关系，可以看到有两个点符合题目规定的条件.

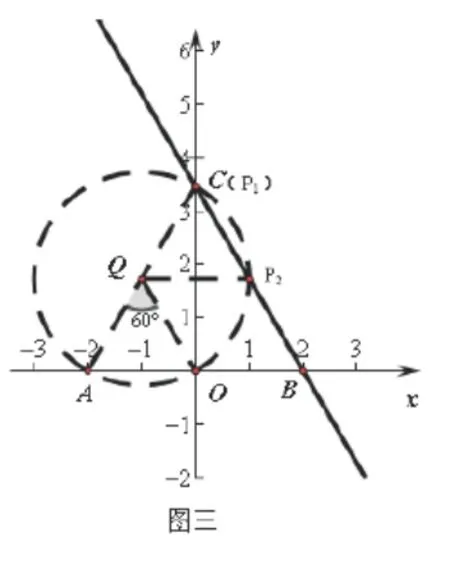
步骤三，对于第（3）小题，是动态几何问题，主要是考查动手操作能力和探索、分析、解决问题的能力．

在动直线BC上寻找符合条件的点P，可在第（2）小题的基础上进一步思考，300的圆周角所对弧为AO，该弧所对的圆心角为600．因此，同样可以通过以AO为弦构造圆进行搭桥，根据对称性原理可知，这样的圆有两个（如图四示），根据“同弧所对圆心角是圆周角的2倍”这一原理得出，符合条件的点P实际上是直线BC与两圆的公共点，这也把问题转化为解决直线与圆的位置关系问题。再通过动手操作，运动直线BC，进行分类讨论，得出直线BC在不同位置时，点P的个数变化．不妨记两圆为⊙Q，⊙Q′，点Q，Q′关于x轴对称，点P的个数情况有四种情况，即有1个、2个、3个、4个.

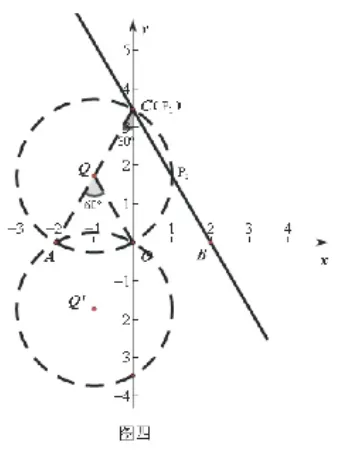
这里，命题者提供本小题的参考答案中，有三处答案值得商榷，应加以修正.

第①处，如下列所示

第①处修正理由：假如点 在⊙Q，⊙Q′这两个圆被轴截成的两段劣弧中（如图五示），则只能使∠APO=150°；假如点P与点A或点O重合时，则∠APO不存在.

所以答案应修正为：

第②、③处，如下列所示：

数学试题参考答案及评分标准 第6页（共8页）

第②处的修正理由：当点P与点A或点O重合时，∠APO不存在，则使∠APO=30°的点P只有两个．

所以答案应修正为：“直线BC过⊙Q与⊙Q′的一个交点，同时与两圆都相交”的部分应属于第2种类；

第③处的修正理由：当直线同时与⊙Q、⊙Q′都相交且不过两圆交点时，将出现两种情形：

一是当直线BC同时与两圆都相交且与弦AO不相交时，则点P有4个；

二是当直线BC与两圆都相交且与弦AO相交，且不过两圆的交点时，从理论上讲应有四个交点，其中与劣弧AO相交的两个点P，使得∠APO=150°，不符合题意，所以点P的个数也只有2个．

所以答案应修正为：

“Ⅳ）有4个：直线BC同时与两圆都相交且与弦AO不相交”；

第二种情形应属于第2类．

通过以上的分析可以看出，本题在参考答案的制作过程中，由于忽略了直线BC与圆的公共点P所形成的角不存在，或在劣弧AO上所形成的∠APO=150°不合题意，导致答案表述不严密.

二、搭桥引路，化动为静

依据辩证法原理，动与静存在着相互对立又相互依存的关系，动依赖静而存在.本题是一道典型的几何动态综合问题，一方面，点在直线上运动；另一方面，直线又在平面上平移.运用构造法是解决本题问题的关键，即根据题设条件和问题的特殊性，构造出一些新的数学形式，搭桥引路，化动态为静态，并借助它们认识并解决原先的问题.构造法具有多种形式，应用范围广，具有灵活性与技巧性，是重要的数学解题方法之一.本题在解题过程中所运用的是构造图形法，通过构造圆搭起动与静的“桥梁“，即以∠APO=30°为前提，构造以AO为弦的圆，目的是通过构造圆这一图形直观地揭示已知与未知的关系，确定论证点P的位置，使证题的思路豁然开朗，就如“山重水复疑无路，柳暗花明又一村”.

本题所体现的考查目标，给了中学数学教学重要启示：教师在课堂教学中，应着力培养学生观察能力，能充分利用已知条件进行严谨推导，从中发现条件与结论的联系，为问题的解决创造条件.在解题教学中，应选取具有代表性的好问题，充分挖掘题目所蕴含的思想价值，给予学生自主学习与合作探究的时空，引导学生审清题意，理清思路，完整解答，通过典型问题这一把“钥匙”开一类“锁”，使学生“做一题、通一类、会一片”，不断提高学生的动态思维、创新思维和想象能力.

（责任编辑：王钦敏）