二维随机分布纤维过滤介质的压力损失分形模型

张　杰， 付海明， 赵洪亮， 雷陈磊， 朱　辉

(东华大学 a. 环境科学与工程学院; b. 国家环境保护纺织工业污染防治工程技术中心， 上海 201620)

二维随机分布纤维过滤介质的压力损失分形模型

张杰a, b， 付海明a, b， 赵洪亮a, b， 雷陈磊a, b， 朱辉a, b

(东华大学 a. 环境科学与工程学院; b. 国家环境保护纺织工业污染防治工程技术中心， 上海 201620)

为了研究影响纤维过滤器压力损失的主要因素，开发了能够生成二维随机分布的虚拟纤维过滤介质的VBA程序，并在纤维随机分布的二维区域中利用计算流体力学(CFD)技术计算了Stokes方程的数值解.通过对虚拟滤料CFD模拟计算结果的数据回归分析可知，纤维过滤介质的压力损失随纤维填充率增加呈非线性增加，与纤维直径的二次方呈反比例关系，与纤维介质厚度及过滤速度呈线性正比例关系，由此提出了二维随机分布纤维过滤介质的压力损失预测模型.在此基础上，考虑了分形维数和迂曲度对过滤压力损失的影响，得出压力损失随分形维数和迂曲度的增加呈非线性增加，提出了包含分形维数、迂曲度的压力损失预测表达式，该表达式与相关文献的分形理论模型具有很高的一致性.

纤维过滤介质； 压力损失； 迂曲度； 分形维数； 随机分布

压力损失是纤维过滤器重要的性能参数，精确的压力损失预测对于纤维过滤器选型以及优化过滤器设计具有重要意义.在过去的50年，学者们建立了众多数学理论以预测过滤器的压力损失.从胞壳模型[1]开始，学者们对纤维规则分布的二维区域进行了详细的研究.但是规则分布模型并不能体现纤维微观结构对于压力损失的影响，因此具有很大局限性，无法反映纤维内部结构(如排列方式、孔隙的连通性、不均匀性)对压力损失的影响.文献[2-4]对有序排列和随机排列的纤维过滤介质进行了研究，表述了微观结构性参数对宏观渗透率的影响.因此，为了定量地分析纤维内部结构对压力损失的影响，近年来，人们开始将迂曲度和分形维数引入对压力损失的预测当中.自从曼德布罗特在20世纪70 年代中期提出分形理论，它就被证明是一种表征多孔介质孔隙结构的有效手段.“分形”一词起源于某些事物在较大的尺度范围内表现出自相似性，并具备一定的分形维数.而引入迂曲度的主要目的是为了对计算的渗透率或阻力系数等参数进行必要的修正，使结果更加接近实际情况.文献[5]对纤维过滤介质截面进行分析，得出分形维数和孔隙率的关系表达式.文献[6]利用差分方法建立了纤维多孔介质的分形渗透率表达式. 文献[7]引入分形维数和迂曲度维数建立了多孔介质的分形渗透率模型.但是对于纤维滤料分形阻力模型的研究并不多见，本文基于二维随机分布纤维过滤介质，采用计算流体力学(CFD)数值模拟方法，研究了纤维过滤介质的压力损失与其主要影响因素的关系，提出了压力损失与纤维填充率、纤维直径、过滤介质厚度以及过滤速度的多元回归关联表达式，并基于分形理论，建立了纤维多孔介质的阻力分形表达式.本研究的意义在于提供了一种二维随机分布纤维过滤介质的压力损失预测模型，该模型考虑了纤维多孔介质的孔隙分布、分形维数、迂曲度特征对压力损失的影响，提出了更加准确预测压力损失的方法，为优化选择滤料提供了理论依据.

1　研究方法

1.1计算模型的建立

开发了二维随机分布的虚拟纤维过滤介质生成的VBA程序，该程序可生成二维的虚拟纤维过滤介质，通过CAD绘制出滤料模型，如图1所示，图中圆圈代表纤维.在虚拟纤维过滤介质生成过程中，可以通过改变圆的数量和直径来控制虚拟纤维过滤介质的填充率.由于圆的位置是随机的，为了获得高质量的网格，纤维之间不允许相互重叠或碰撞，纤维之间的最小间距为0.1df，df表示纤维直径.由于气流进入和离开纤维阵列时速度和流向会发生剧烈变化，而这些变化会影响方形纤维阵列两侧的流场，因此在纤维过滤介质两侧分别设置0.4H(H为过滤介质厚度)的区域，以反映该区域流场变化带来的压力损失.

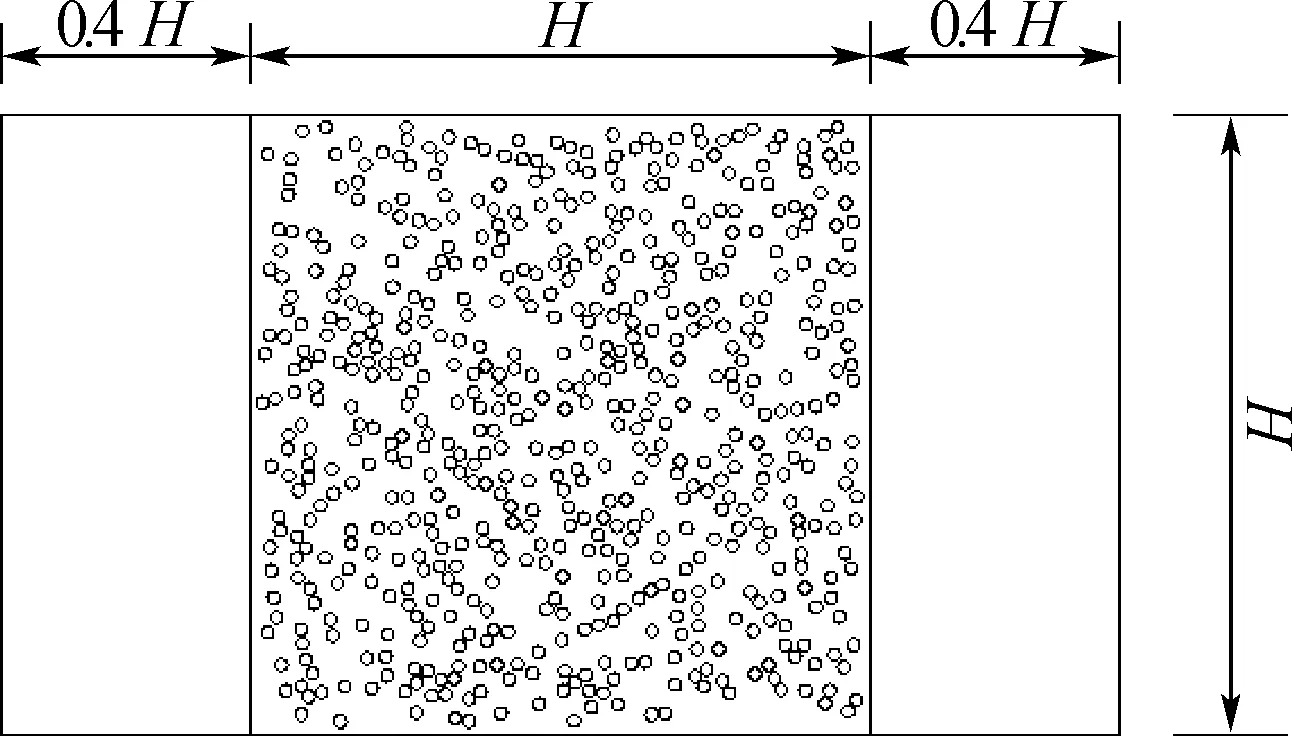
图1　纤维二维随机分布模型Fig.1　2D random distribution fiber model

1.2边界条件的定义和网格划分

将气流进入的边界设置为速度入口，气流出口设置为压力出口，两侧的边界设置为对称边界条件，本文使用局部加密的三角形网格对计算区域进行划分.对于网格尺寸的设置，文献[2]进行了网格无关性的测试，结果显示当纤维壁面分布50个以上网格时，压力损失模拟值不再随网格尺寸发生变化.因此在本文中，纤维壁面的网格尺寸为0.02πdf，网格尺寸从壁面处向周围逐渐增大，最大尺寸为0.1df.

1.3模型计算

一般纤维滤料的填充率为1%～30%，滤料纤维的平均直径为0.5～20.0 μm[8].在本研究中为了覆盖尽可能多的范围，试图建立尽可能大的纤维填充率，而在圆形纤维模型中，理论上所能达到的最大填充率为π/4，即0.785，又限于随机排列不重叠的原则，填充率很难达到50%，经过反复试验，最终确定最大填充率为44%.由此本文在H=250和1000 μm 的两组模型中分别建立了填充率分别为5%， 6%， 10%， 12%， 15%， 18%， 20%， 24%， 25%， 31%， 44%，纤维直径为2.5， 5， 10， 20， 40 μm 的55组模型.过滤速度为0.2～1.6 m/s.

1.3.1阻力计算

采用CFD软件求解流动区域的Stokes方程：

(1)

(2)

(3)

其中：p为过滤气体的压力；u和v分别为沿x轴和y轴方向的过滤气体的速度分量；μ为过滤气体的黏度.

通过求解上述方程得到各点的压力值，将进口压力与出口压力相减即为计算模型的压力损失值.

1.3.2迂曲度计算

迂曲度(τ)的定义[9]为

(4)

其中：Lt为流体路径的实际长度；L0为沿宏观压力梯度方向上的直线长度或样品的厚度.

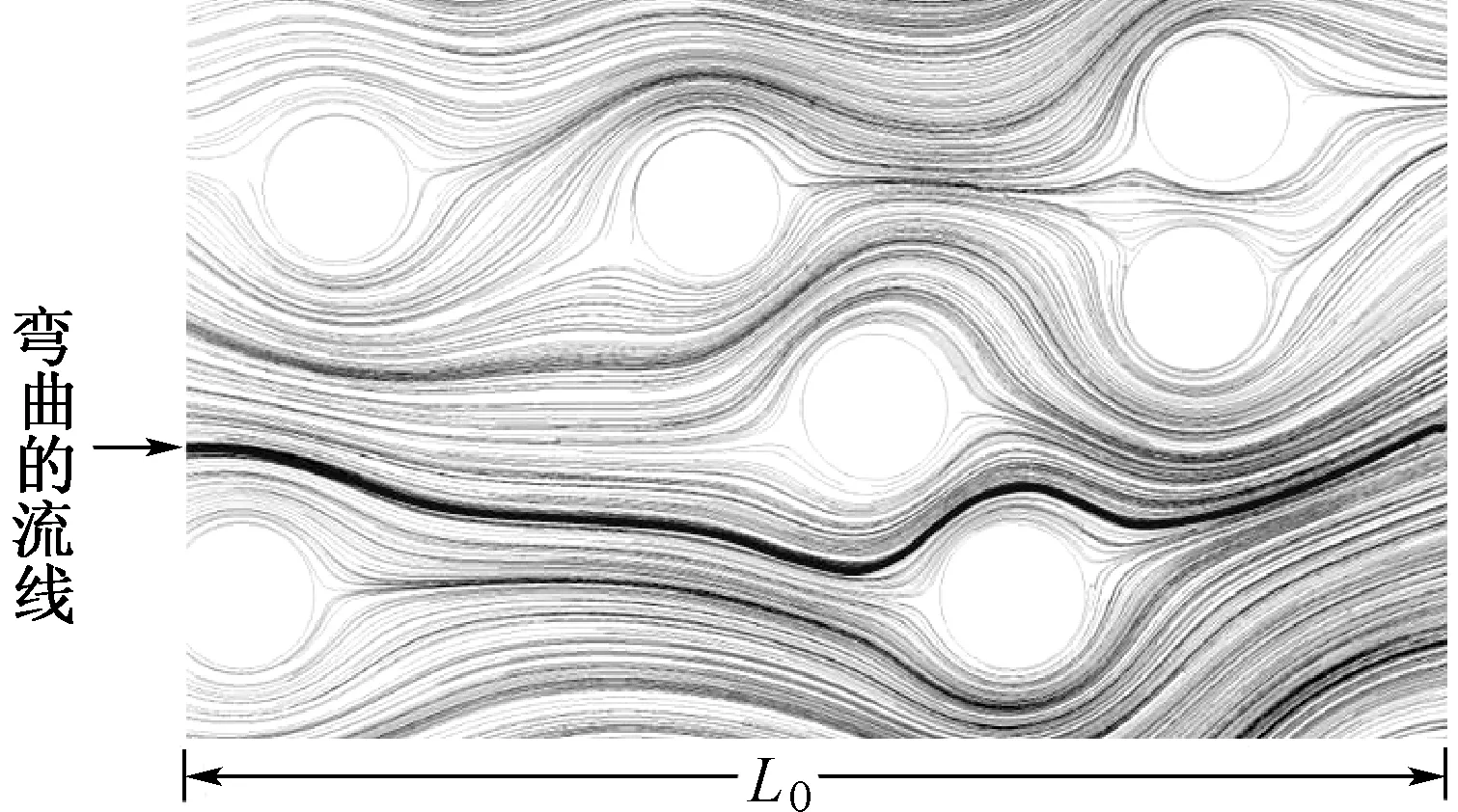
图2　多孔介质里的弯曲流线Fig.2　Tortuous line in porous media

本文利用有限元法对模型进行数值模拟，以得到模型的流线.然后选取具有代表性的流线进行统计计算，根据式(5)加权平均得到各个模型的迂曲度.

(5)

其中：N为所选取的流线数量.

1.3.3分形维数计算

虽然豪斯道夫维数是目前使用最广泛的分形定义，但是很多情况下豪斯道夫维数难以求解，因此许多等价的维数定义被提出，如计盒维数、半径维数等.本文利用Fractalfox软件计算了模型的计盒维数.

采用程序生成的CAD随机滤料模型作为计算样本，首先将CAD图像导出为.eps封装文件，然后使用Photoshop软件把源文件处理为尺寸780像素×780像素的黑白二值图像，最后将图像保存为BMP格式图形文件.将样本导入Fractalfox软件，计算其计盒维数.通过划分图像形成网格，最小网格尺寸为2,最大网格尺寸为100，统计出不同网格尺寸下网格中包含的盒子数.所要计算图形的分形维数由式(6)确定.

(6)

其中：M为常数；r为网格尺寸；D为分形维数.对式(6)两边同时取对数后得到：

logN(r)=-D·logr+logM

(7)

再通过线性回归求出logN(r)相对于logr的斜率，也就是该图像区域的计盒维数[6].

2　模拟结果和讨论

根据达西定律，纤维过滤器的压力损失Δp是一个与过滤器迎风速度v、纤维直径df、过滤器填充率c、过滤介质厚度H有关的函数，如式(8)所示.

(8)

其中：f(c)为无量纲压力损失，它仅是填充率的函数.以往的研究中，众多学者给出了f(c)的不同形式.文献[1]计算了由规则矩阵组成的纤维流场，得到了经典的单元模型，其无量纲压力损失f(c)表达式为

(9)

文献[10]数值求解了圆柱形纤维周围的流场，给出的无量纲压力损失表达式为

(10)

文献[11]综合以往的试验及研究数据给出的无量纲压力损失表示为

(11)

式(11)适用于填充率为0.6%～30%的情况，是工程界普遍接受的一个压力损失预测模型.

文献[12]计算了三维随机分布过滤模型的流场，得到了三维情况下的无量纲压力损失表达式为

(12)

式(12)适用于填充率小于25%的情况.

本文根据CFD模拟计算的结果，采用自定义的非线性回归方法对数据进行回归分析,提出了二维随机模型的压力损失表达式为

(13)

R2=0.97

(14)

其中：R2为相关系数，其值为0.97，可见回归方程与数据之间具有良好的相关性.

将数值模拟得到的数据与经典模型进行对比，结果如图3所示.由图3可以看出，无量纲阻力模拟值与文献[11]的模型计算结果十分接近，而文献[1, 10]的模型计算结果过高预测了滤料压力损失，并且随着填充率的增大，不同模型的压力损失差异越来越大，由此可见纤维规则分布的压力损失要高于纤维随机分布的压力损失.一个纤维随机分布滤料模型的流场如图4所示.由图4可以发现，在随机模型中出现了一些纤维聚集的区域，文献[2]称之为纤维簇，这种分布现象在规则分布模型中是不存在的.在纤维簇的周围，气体的流动被阻滞，并以很低的速度通过，而在纤维簇与纤维簇之间的区域形成了一些宽阔的流通通道，气体从这些通道高速通过.这些高速流体带来的惯性力削弱了纤维簇对流体的阻滞力，由此可以解释无量纲阻力模拟值与文献[1]模型的差异.与文献[12]相比，二维随机模型无量纲阻力模拟值要略大于三维模型模拟值，但是差异仅约1%，可见二维随机模型能够比较准确地预测真实滤料的压力损失.相比较三维模型巨大的运算量，二维模型可以在保证结果精度的前提下大大减少运算量和运算时间.

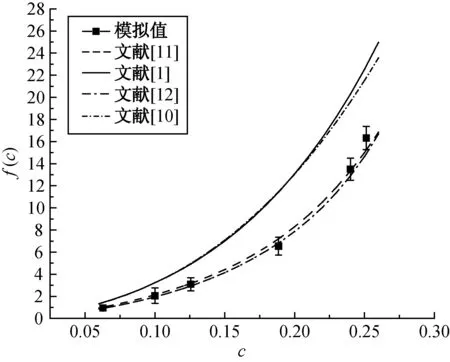
图3　模拟结果与经典模型的对比Fig.3　Comparison of simulation results and classic models

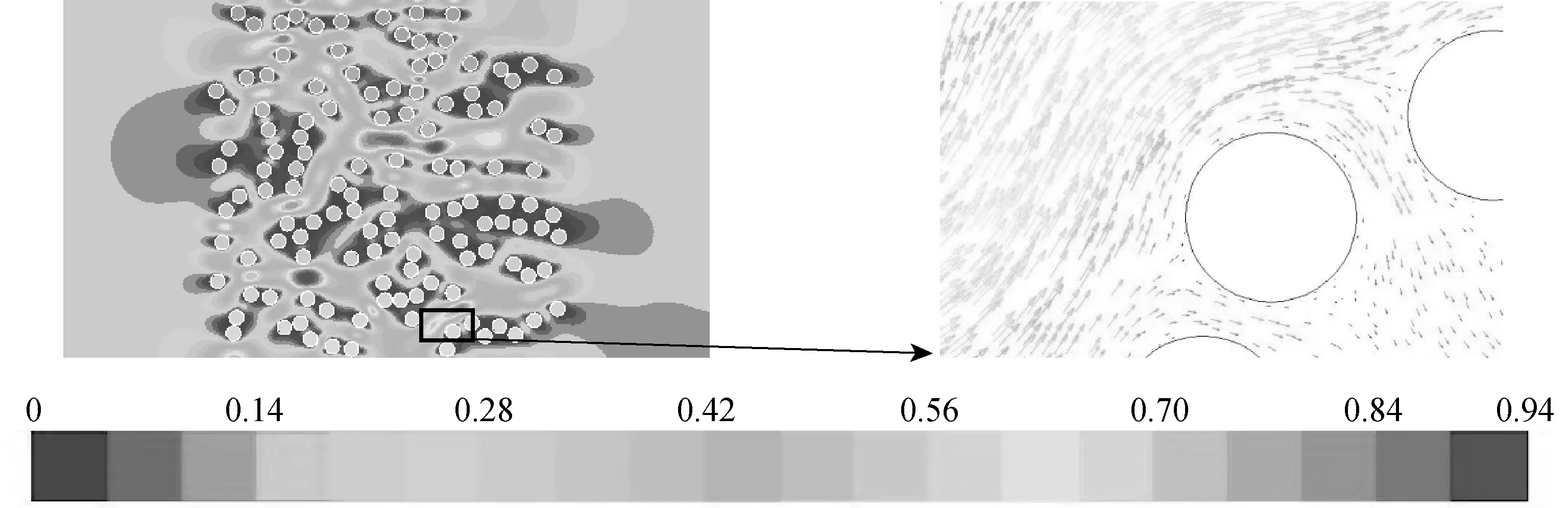
图4　过滤速度矢量图(df=10 μm， c=15%， v=0.2 m/s)Fig.4　The filtration velocity vector diagram(df=10 μm, c=15%, v=0.2 m/s)

当引入分形维数和迂曲度后，根据模型的测量结果得到了包含分形维数和迂曲度的二维随机模型压力表达式为

R2=0.94

(15)

文献[6]采用差分方法提出了纤维多孔介质渗透率的分形模型，其压力表达式为

(16)

由式(15)和(16)计算的压力损失随分形维数、迂曲度和填充率的变化如图5～7所示.由图5～7可知，由式(15)和(16)计算的压力损失吻合良好，平均偏差不超过7%，并且压力损失均随分形维数、迂曲度和填充率的增大而增大.

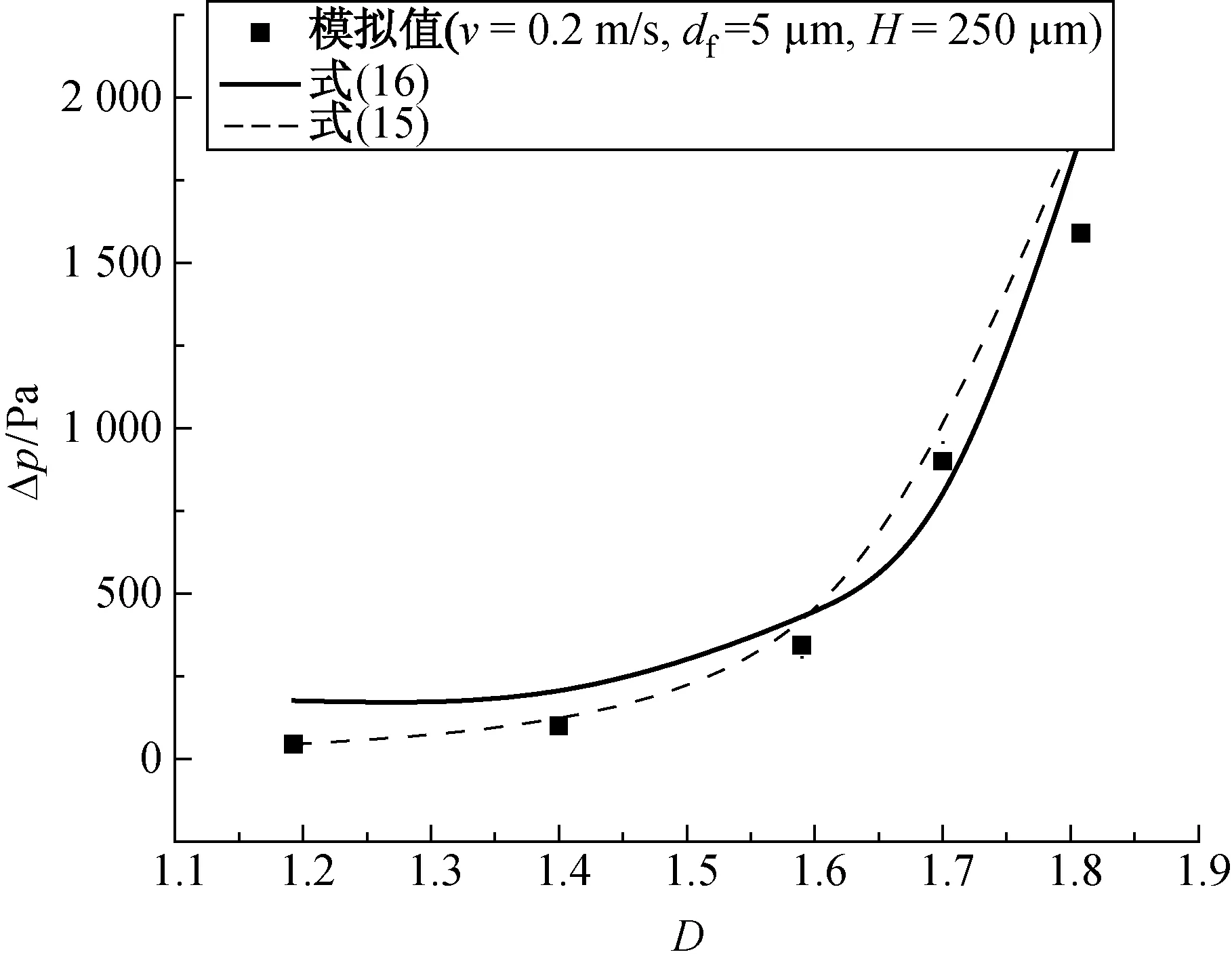
图5　分形维数与压力损失的关系Fig.5　The relationship between the fractal dimension and the pressure loss

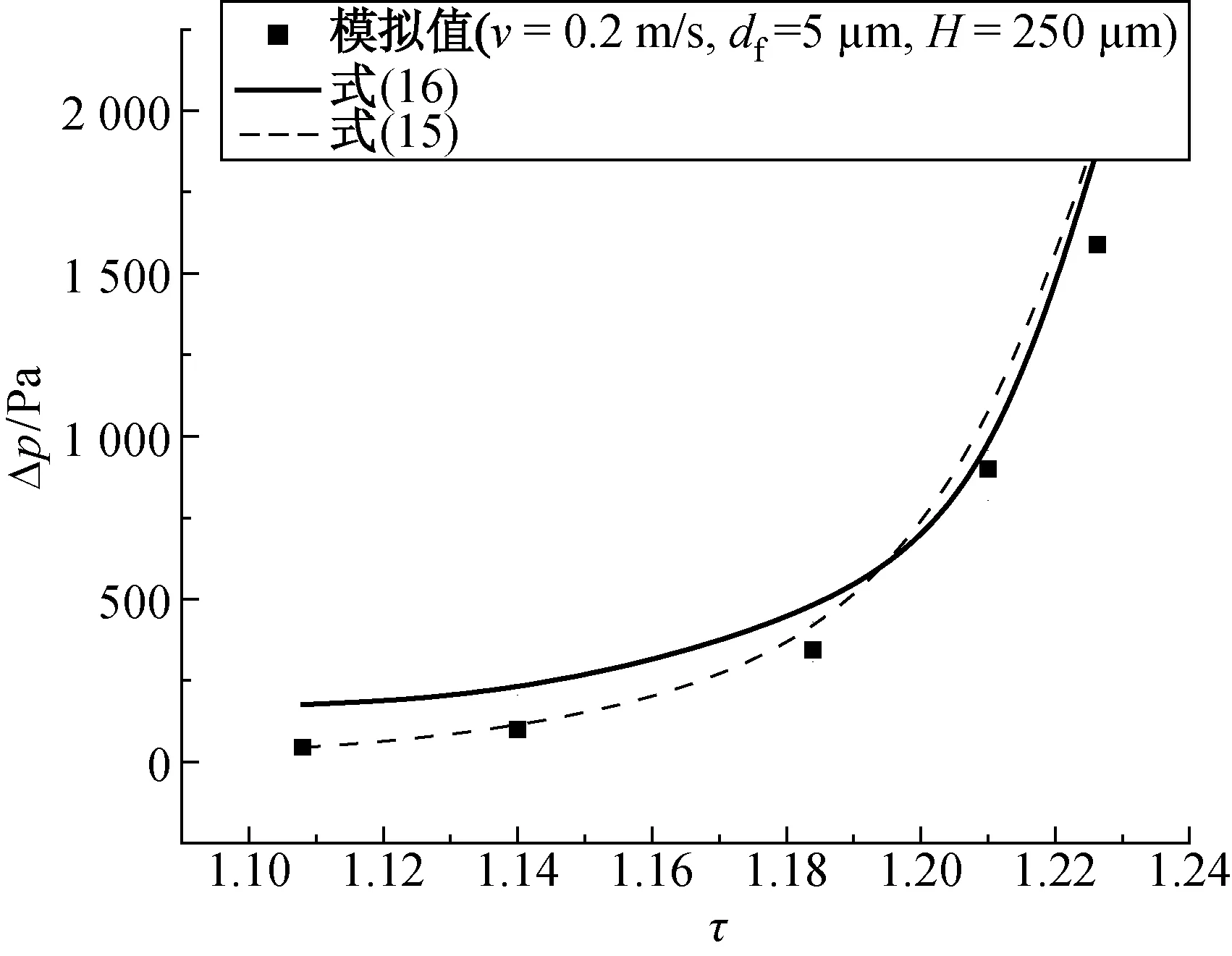
图6　迂曲度与压力损失的关系Fig.6　The relationship between the tortuosity and the pressure loss

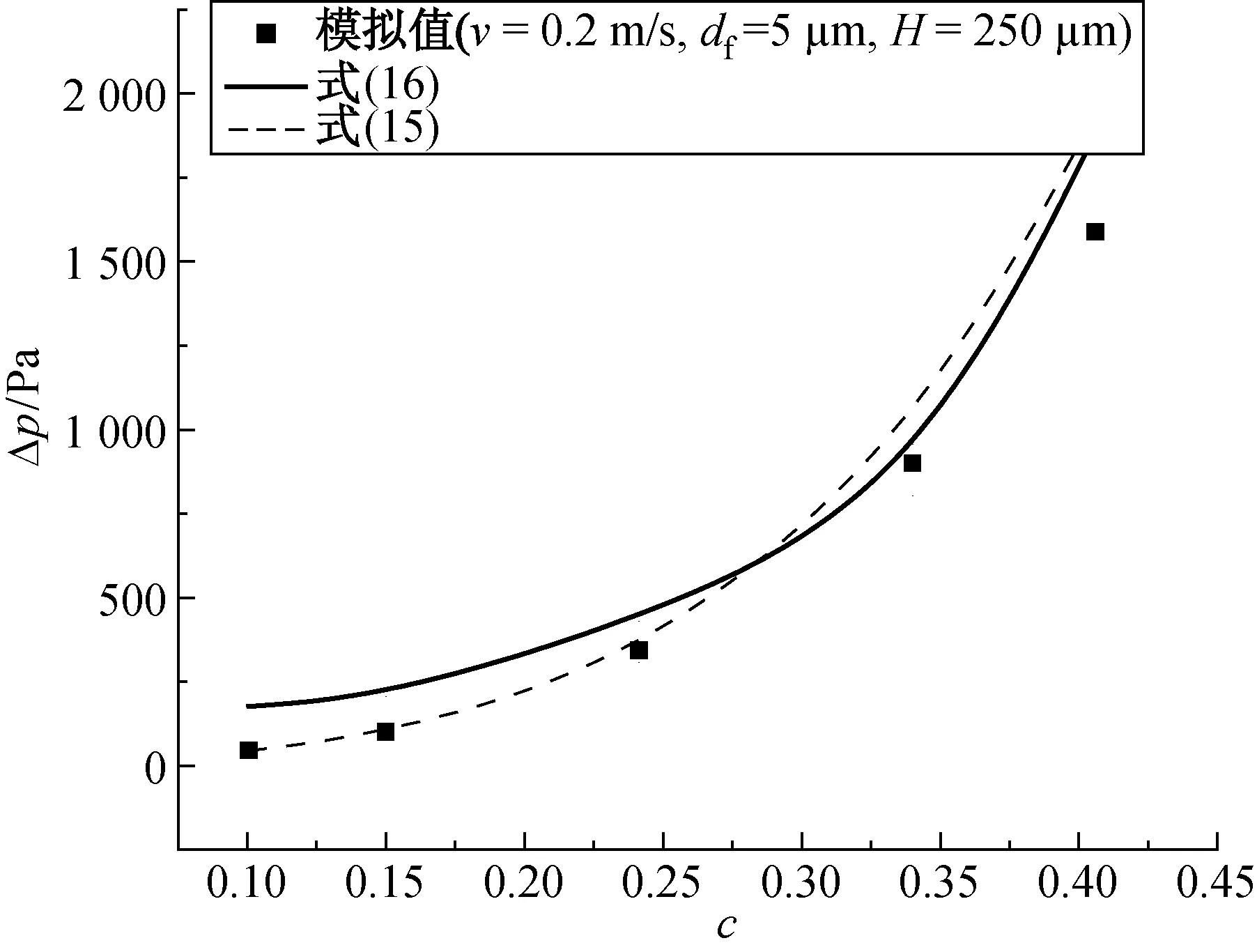
图7　填充率与压力损失的关系Fig.7　The relationship between the solid volume fraction and the pressure loss

3　结　语

针对二维随机分布纤维过滤介质，本文对数值模拟得到的大量数据进行了回归分析，分别得到了二维随机分布模型压力损失的一般表达式和分形表达式，并与以往的研究进行了对比，显示出较高的一致性，并得到以下结论：

(1) 二维随机模型预测的压力损失要低于二维规则分布模型，但略高于三维随机模型；

(2) 压力损失与纤维填充率呈非线性正比例关系，与纤维直径的二次方呈反比例关系，与纤维介质厚度及过滤速度呈线性正比例关系；

(3) 随着分形维数和迂曲度的增大，过滤介质的压力损失均呈非线性增加.

[1] KUWABARA S. The forces experienced by randomly distributed parallel circular cylinders of spheres in a viscous flow at small Reynolds number[J].Journal of the Physical Society of Japan, 1959, 14(4): 527-532.

[2] YAZDCHI K, SRIVASTAVA S, LUDING S. Microstructural effects on the permeability of periodic fibrous porous media[J]. Multiphase Flow, 2011, 37(8): 956-966.

[3] YAZDCHI K, SRIVASTAVA S, LUDING S. Micro-macro relations for flow through random arrays of cylinders[J]. Composites Part A, 2012, 43(11): 2007-2020.

[4] YAZDCHI K, LUDING S. Towards unified drag laws for inertial flow through fibrous materials[J]. Chemical Engineering Journal, 2012, 207/208(10): 35-48.

[5] 李岩,付海明,张健.纤维过滤介质孔隙率及其分形维数[J].建筑热能通风空调,2012,31(4):18-21.

[6] ZHOU D H, FAN J T, DING F. A difference-fractal model for the permeability of fibrous porous media[J]. Physics Letters A, 2010, 374(10): 1201-1204.

[7] YU B M, CHENG P. A fractal permeability model for bi-dispersed porous media[J]. Heat Mass Transfer, 2002, 45(7/8): 2983-2993.

[8] KIM J. Investigation on charge deterioration of electrically charged filter media using electric force microscopy[D]. USA: NC State University, 2005:1-169.

[9] BEAR J. Dynamics of fluids in porous media[M]. New York: Dover Publications, 1988.

[10] RAO N, FAGHRI M. Computer modeling of aerosol filtration by fibrous filters[J]. Aerosol Science and Technology, 1988,8(2): 133-156.

[11] DAVIES C N. Air filtration[M]. London: Academic Press, 1973: 1-171.

[12] JACKSON W G, JAMES F D. The permeability of fibrous porous media[J]. The Canadian Journal of Chemical Engineering, 1986, 64(3): 364-374.

A Fractal Model for the Pressure Drop of 2D Random Distribution Fiber Filter Medium

ZHANGJiea, b,FUHai-minga, b,ZHAOHong-lianga, b,LEIChen-leia, b,ZHUHuia, b

(a. School of Environmental Science and Engineering; b. State Environmental Protection Engineering

Center for Pollution Treatment and Control in Textile Industry, Donghua University, Shanghai 201620, China)

In order to study the main factors influencing the fiber filter pressure drop, the VBA program which can generate 2D random distribution fiber medium is developed and the numerical solutions of Stokes equations in the area of 2D fiber are calculated using the computational fluid dynamics(CFD) technology. Through regression analysis of the calculated data, it is concluded that the pressure drop of fiber filter medium presents nonlinear direct ratio relation with the solid volume fraction, inversely proportional relationship with the diameter of the square, linear direct ratio relation with the medium thickness and filtration velocity, and a two-dimensional random distribution fiber filter medium pressure drop prediction model is put forward. In addition, the fractal dimension and tortuosity are also considered to the influence of the filter pressure drop. It is concluded that the pressure drop of fiber medium presents nonlinear relation with the fractal dimension and tortuosity. In the end, a fractal pressure drop prediction expression is put forward. This expression has a very high consistency with the theoretical models which are obtained by different methods.

fiber filter medium; pressure drop; tortuosity; fractal dimension; random distribution

1671-0444(2015)06-0829-05

2014-09-29

国家自然科学基金资助项目(51178094，41371445)；广西教育厅科研基金资助项目(201106LX724)

张杰(1990—)，男，山东东营人，硕士研究生，研究方向为通风空调与气体净化.E-mail：zhangjie1990222@126.com

付海明(联系人)，男，高级工程师，E-mail：fhm@dhu.edu.cn

TS 179

A