基于拉-压杆模型的花瓶墩墩顶拉力简易估算方法
2015-08-24潘一平刘淑敏巩美杰
潘一平,刘淑敏,巩美杰
(1.南京禄口国际机场有限公司,江苏 南京 210006;2.苏交科集团股份有限公司,江苏 南京 201117)
基于拉-压杆模型的花瓶墩墩顶拉力简易估算方法
潘一平1,刘淑敏2,巩美杰2
(1.南京禄口国际机场有限公司,江苏 南京 210006;2.苏交科集团股份有限公司,江苏 南京 201117)
以南京禄口国际机场站前高架圆端形花瓶墩为背景,采用有限元程序midas FEA对其建立实体有限元模型,对不同构造尺寸的花瓶墩进行受力分析。按照杆件中心与应力迹线重合的准则构建了墩顶拉-压杆模型,得到拉-压杆夹角θ的近似计算方法,进而得到花瓶墩墩顶拉力的简易计算方法。通过对墩帽半径R及墩帽高度H的参数分析,证明了文中所提供的方法能够满足工程精度要求。
高架桥;花瓶墩;拉-压杆模型;有限元分析
花瓶墩不仅造型美观、通透性好,同时墩身占地面积小,易于桥下地面道路的设计。因此,花瓶墩在我国城市桥梁中得到了广泛应用。但在墩顶支座反力的作用下,墩顶在一定范围内产生拉应力,如果设计不当,墩顶有可能产生裂缝,影响结构的耐久性甚至结构安全。目前对于花瓶墩墩顶扩大段的设计计算,多数是参照《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62—2004)》中桩基承台的“撑杆-系杆体系”进行设计计算。但由于计算参数取值不明确,计算结果偏差较大。
拉-压杆模型法已经被大量实验研究证明是混凝土结构设计的通用方法,能用于任何混凝土结构及荷载情况的结构设计,尤其对于受力较复杂而不符合平截面假定的区域“D区”是十分简单和实用的计算方法[1]。本文以南京禄口国际机场站前高架圆端形花瓶墩为背景,采用有限元程序midas FEA对其建立实体有限元模型,对不同构造尺寸的花瓶墩进行受力分析,建立墩顶拉-压杆模型,对花瓶墩墩顶拉力进行计算。
1 花瓶墩拉-压杆模型
根据混凝土结构是否符合伯努利(Bemoulli)平面应变假定,可将其分为“B区”与“D区”两个区域。“B区”是指截面应变分布基本符合平截面假定的结构区域,B表示梁或伯努利,其截面应力状态可以通过内力得出。在未开裂时截面应力可借助于截面性质(如面积、惯矩等)来计算,开裂后,则可应用桁架模型来分析。“D区”是指截面应变分布呈现明显非线性的结构区域,包括因截面突变而形成的不连续点附近区域或集中力作用点附近区域,这些区域具有力流受挠动的特点,D表示不连续、扰乱或细节。从弹性阶段开始平截面应变假定在这些区域就已不再成立,随着荷载的增加,梁截面的抗弯塑性发展模型不能够揭示其破坏机理。而拉-压杆模型法是被国内外大量实验研究证明的针对“D区”简单实用的计算方法[2]。
1.1有限元分析
南京禄口国际机场站前高架圆端形花瓶墩结构尺寸如下:桥墩直线段墩身宽210 cm,厚度150 cm,侧面圆端形半径75 cm;墩帽扩大段由两段与墩身相切的圆弧线形成,高300 cm,顶宽350 cm,支座间距210 cm,支座垫石平面尺寸70 cm×70 cm,厚15 cm。桥墩构造图如图1所示。采用midas FEA建立实体有限元模型进行受力分析,如图2所示。
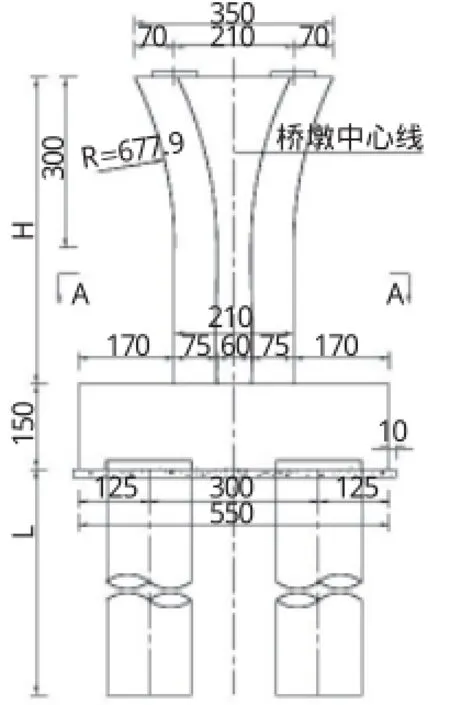
图1 花瓶墩立面构造图 (单位:cm)

图2 花瓶墩有限元模型图
模型参数如下:单个支座设计支反力N=6 000 kN,按均布荷载施加于70 cm×70 cm的支座垫石上,左右对称加载,桥墩底部固结。桥墩混凝土为C40,弹性模量3.25×104MPa,容重25 kN/m3,泊松比0.167。计算不计普通钢筋影响,不考虑材料及几何非线性。得到墩顶主应力等值线云图如图3、图4所示,主应力迹线如图5、图6所示。

图3 主压应力云图

图4 主拉应力云图

图5 主压应力迹线图
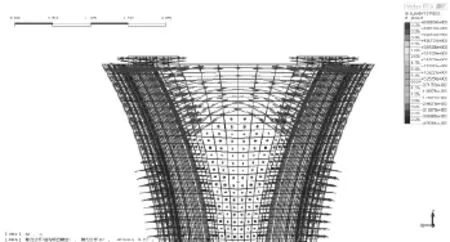
图6 主拉应力迹线图
通过对图6桥墩中心截面正应力积分,得到墩顶横向拉力合力T=2 259 kN。
1.2拉-压杆模型建立[3]
结合有限元模型得到的墩顶区域主应力迹线图,按照杆件中心尽量与应力迹线重合的准则来构建花瓶墩墩顶拉-压杆模型。拉杆设置于墩顶主筋形心位置,以实线表示;压杆沿主压应力迹线设置,以虚线表示;形成拉-压杆模型如图7所示。
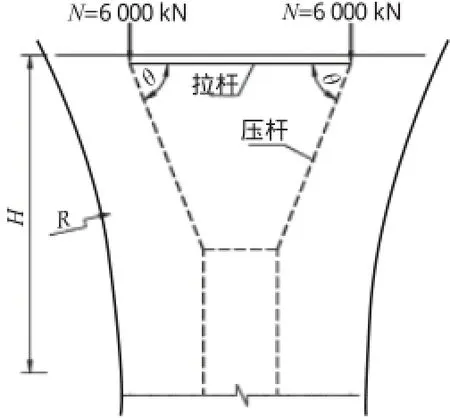
图7 墩顶区拉-压杆模型示意图
1.3拉-压杆夹角θ确定[4-5]
上述建立的拉-压杆模型不具唯一性,拉杆、压杆的内力大小随着夹角θ的变化而变化,然而在确定荷载作用下,结构内部的变形及应力是唯一的。因此,夹角θ的确定是拉-压杆模型优劣的关键。Schlaich曾提出了判别拉压杆模型优劣的两个准则[6]:
(1)拉杆、压杆的中心应尽量与应力迹线重合。这样可以减少结构在受力过程中的应力重分布,并且保证钢筋配置在裂缝最可能产生的区域。
(2)最小应变能准则。拉压杆模型的应变能绝大部分集中于拉杆,因此拉杆总长度最小的拉压杆模型是最优的模型。
文献[1]对夹角θ与花瓶墩几何尺寸之间的关系进行过一些推导,具有一定参考意义;文献[4]根据最小余能原理,通过迭代求解得到结构应变余能极值来确定夹角θ。以上方式均能得到唯一的拉-压杆模型,但参数取值存在一定主观性,迭代过程计算量大,十分繁琐。
本文通过对不同几何尺寸的桥墩进行计算分析,发现各模型在墩顶以下H/3范围内,单元主拉应力方向与桥墩侧面圆弧法线同向。因主压应力与主拉应力垂直,主压应力方向即为该范围的切线方向。因此模型压杆方向即为侧面圆弧切线方向。为简化计算,本文近似取H/3中点处,即H/6处圆弧切线方向为压杆方向。
桥墩几何关系如图8所示,墩顶侧面弧线AC是以O为圆心,R为半径的圆弧线,墩帽高度为H。取H/6处圆弧为A点,自A点作OC的垂线,垂足为B,自A点作圆弧AC的切线AD,交OC延长线于D,由相似三角形原理可得到拉-压杆夹角θ的表达式为:
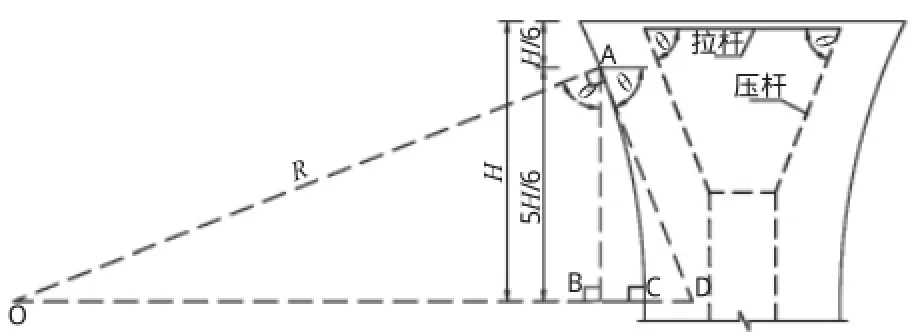
图8 墩顶几何关系图
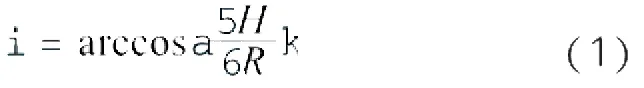
由式(1)求得拉-压杆夹角θ,再根据节点平衡原理,得到模型拉杆内力设计值T为:

模型压杆内力设计值D为:

式中:N为单侧支座反力设计值。
得到拉、压杆内力设计值后,可参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》中的方法进行配筋设计及混凝土压应力验算。
2 参数分析
2.1对墩帽半径R的参数分析
以墩帽半径R为参数对不同桥墩进行计算分析。R值改变时保持支座位置与墩帽边缘距离不变,其余尺寸如图1所示。对桥墩中心截面正应力进行积分得到墩顶拉力合力T,根据节点平衡原理得到拉-压杆夹角θ;按式1计算拉-压杆夹角θ ',式(2)计算墩顶横向拉力合力T '。以R为X轴,T(T ')及θ(θ ')为Y轴,将表中结果绘于直角坐标系如图9、图10所示。

图9 R-T(T ')关系图
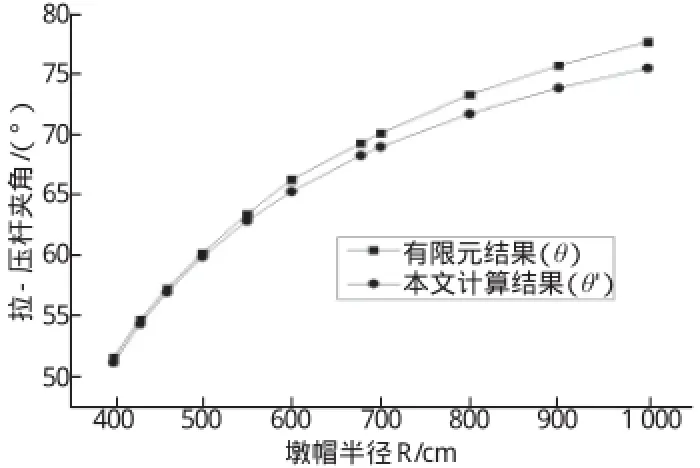
图10 R-θ(θ')关系图
由图可知,本文提供的计算方法与有限元计算结果相差不大,且走势一致;当其他条件不变时,随着墩帽半径R的增大,墩顶拉力T非线性减小,拉-压杆夹角θ非线性增大;除墩帽半径R较大(R>800 cm)时计算结果偏差较大外,均能够满足工程精度要求。
2.2对墩帽高度H的参数分析
以墩帽高度H为参数对不同桥墩进行计算,其余尺寸如图1所示。计算结果如
图11、图12所示。
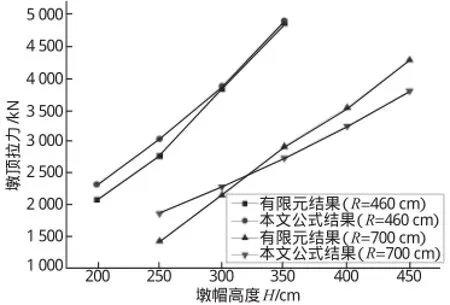
图11 H-T(T ')关系图
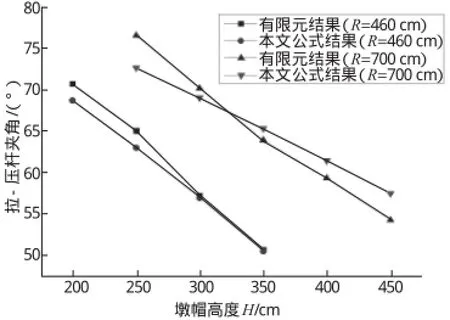
图12 H-θ(θ')关系图
由图可知,本文提供的计算方法与有限元计算结果走势基本一致;当其他条件不变时,墩帽高度H与墩顶拉力T成正比例关系,与拉-压杆夹角θ成反比例关系。
3 结语
本文通过对不同构造尺寸的圆端形花瓶墩进行受力分析,建立了墩顶拉-压杆模型。得到了拉-压杆夹角θ的近似计算方法,进而提出了花瓶墩墩顶拉力的简易计算方法。通过对墩帽半径R及墩帽高度H的参数分析,证明本文所提供的方法与有限元计算结果相差不大,且曲线走势一致。除墩帽半径R较大(R>800 cm)时计算结果偏差较大外,均能够满足工程精度要求。有限元计算时未考虑钢筋对拉-压杆模型的影响,待后续研究。本文所示方法仅适用于类似构造条件下花瓶墩的简易计算,不具通用性。
[1]李新平,周晶,张勇.薄壁花瓶墩的拉力计算实用方法[J].昆明理工大学学报(自然科学版),2011,36(2):32-37.
[2]周履.压杆-拉杆模型在混凝土结构设计中的应用[J].世界桥梁,2002(2):1-7.
[3]郑楷柱.花瓶墩的拉压杆模型设计方法研究[J].中国建材科技,2011(3):39-41.
[4]丁印成,张茜茜,王彤凝.花瓶墩墩顶受力特性分析[J].低温建筑技术,2014,36(5):97-100.
[5]胡剑,程龙.基于拉压杆模型的花瓶桥墩受力分析[J].公路,2012(5):175-178.
[6]Schlaich J,Sch fer K,Jennewein M. Toward a Consistent Design of Structural Concrete[J]. Journal ofthe Prestressed Concrete Institute,1987,32(3):74-150.
Estimation Methods for Pier Top Tension of Vase Pier Based on Strut-and-tie Model
Pan Yiping1, Liu Shumin2, Gong Meijie2
(1.Nanjing Lukou International Airport Co, Ltd.,Nanjing 210006, China; 2. JSTI Group, Nanjing 210017, China)
Based on the elevated rounded shape vase piers of Nanjing Lukou international airport station, the solid finite element models of the piers were established by finite element program Midas FEA in this paper, and the stress analysis was carried out on the different size of vase piers. The pier top strut-and-tie model was built according to the overlap criterion of the bar center and the of stress trajectory. An approximate calculation method of the strut-and-tie angle theta was got, and then a simple calculation method for pier top tension of the vase pier was got. Through the parameter analysis of the pier cap radius R and height H, it was proved that the methods provided in this paper could satisfy the precision requirement in engineering.
viaduct; vase pier; strut-and-tie model; FEA
U442.5
B
1672-9889(2015)04-0042-03
潘一平(1965-),男,上海人,高级工程师,主要从事南京禄口国际机场新建、改扩建工程的建设管理等工作。
(2015-07-07)
