双互动四统一教学范式下课堂创造环节设计方法探究
2015-08-24孟庆香延边第二中学吉林延吉133000
孟庆香(延边第二中学,吉林 延吉 133000)
双互动四统一教学范式下课堂创造环节设计方法探究
孟庆香
(延边第二中学,吉林 延吉 133000)
创造环节作为双互动四统一教学范式五个环节中的一个环节,主要是对整节课教学效果的检验和对各课堂环节的升华,在整节课中起到画龙点睛的作用。创造环节的实现形式灵活多样,主要有课堂游戏、变式训练和开放讨论等。
双互动四统一;创造;有效教学
“双互动四统一”教学模式是具有延边二中特色的课堂教学及课外导学模式。延边教育学院学报》2010年第6期《“双互动四统一”教学范式探析》一文对此教学模式有详尽阐述。“双互动四统一”教学模式分课内显性互动和课外隐性互动。其中,创造是课内显示互动中及其重要的一个环节。
一、创造环节的诠释
课内显性“互动式”共分五个阶段:问题阶段—发散阶段——收敛阶段——综合阶段——创造阶段。
在“创造”环节中,教师点拨、引入验证,组织课堂活动;学生验证结论、解决问题、创新学习。教师是本阶段的倾听者和组织者;学生是课堂的主体力量,是本阶段的实施者和执行者。
二、创造环节的实现形式
创造环节作为五个环节中的最后一个环节,主要是对整节课教学效果的检验和对各课堂环节的升华,在整节课中起到画龙点睛的作用。“创造”环节的实现形式灵活多样,主要有:课堂游戏、变式训练和开放讨论等。
1.课堂游戏——巩固基础,激发学习积极性
课堂游戏常常因其趣味性可以极大地吸引学生参与课堂,将枯燥的数学变成妙趣横生的知识。如若“创造”环节能合理设计,可以事半功倍地提升课堂效率,加强学生对基础的巩固和加深对知识的理解,提高知识的应用能力。并极大地激发学生学习的潜力和创造力。
教学案例:王老师教学《椭圆的简单几何性质》一课时在“创造”环节中设计了“课堂游戏”:全班同学分成三个学习小组,教师准备了十道椭圆有关问题,答对加十分,答错不扣分,得分最高的组会得到物质奖励和“雷鸣般”的掌声。题目如下:
1.椭圆离心率公式是什么?
2.椭圆中cba,,的关系是什么?
3.椭圆离心率越接近于0会越扁还是越圆?
4.椭圆顶点坐标是什么?
5.椭圆的对称轴是什么?对称中心是什么?
6.长半轴轴长是多少?
10. 已知椭圆的一个焦点与短轴两顶点组成一个等边三角形,求椭圆的离心率。
王老师通过十个逐层递进的问题,采用抢答的方式,在集体荣誉感的激励下,学生积极思考、回答,充分参与课堂,高效地实现了“创造”环节。整节课生动活泼。
2.变式训练——拓宽思维的广度与拓展思维深度
变式训练主要通过改变条件、改变结论或条件结论互换的方式把一个看似孤立的问题从不同角度向外扩散,形成一个有规律可寻的系列,帮助学生在问题的解答过程中去寻找解类似问题的思路、方法。充分利用变式训练的优势实施“创造”环节,可以使课堂生动活泼,有助于拓宽思维的广度和拓展思维深度,进而实现有效教学。
教学案例:案例1.在高三复习课《直线与圆、圆与圆的位置关系》中,“创造”环节采用如下变式训练:
题目:在平面直角坐标系 xoy中,已知圆x2+y2=4上有且只有四个点到直线12x-5y+c=0的距离为1,求实数c的取值范围。
变式训练1:在平面直角坐标系xoy中,已知圆x2+y2=c2上有且只有四个点到直线12x-5y+13=0的距离为1,求实数c的取值范围。
变式训练2:在平面直角坐标系xoy中,已知圆x2+y2=4上几个点到直线12x-5y+c=0的距离为1?
变式训练3:在平面直角坐标系xoy中,已知圆x2+y2=c2上有几个点到直线12x-5y+13=0的距离为1?
通过四个题目的比较,学生可以深刻的理解动圆定直线和定圆动直线问题在解题方法上的异同。并能在解决动圆定直线问题的基础上,激发学生的创造力去探索定圆动直线的解题方法,进而探索点的个数问题。
案例2. 在高三复习课《圆的方程》中,“创造”环节采用如下变式训练:
题目:已知点M(1,0)是圆C:x2+y2-4x-2y =0内的一点,求过点M 的最短弦所在的直线的方程。
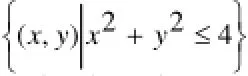
变式训练2:直线y=kx+3与圆(x-2)2+(y-3)2=4相较于M,N两点,若,求k的取值范围。
以上三个题目都是最短弦长问题,学生通过三个题目的比较不断拓宽思维的广度和拓展思维深度,实施“创造”环节,实现有效教学。
3.开放讨论——理论联系实际,自由发挥
开放式问题往往没有固定的模式和标准答案,学生可以根据自己对知识的理解选择一个角度对问题进行阐述,学生可以充分发挥自己的想象力,结合自己所长,将数学问题与生活常识、化学知识、物理知识、生物知识等充分联系,拓展思维。

案例1.《抛物线及其标准方程》一节图象、方程、焦点、准线共有四组,学生经常混淆。课上教师设置问题:“请仔细观察四组图形、分析其方程、焦点、准线的异同,尝试总结记忆方法。”学生认真观察,各抒己见,方法各异,十分踊跃。有的同学发现所有的左边都是二次的,右边都是一次的;有的同学发现焦点非零项恰好与一次项字母一致;有的同学发现准线值与焦点左边非零值互为相反数,如此等等,经过全班同学共同讨论,总结,最后确定最佳记忆方法:(1)形式特征:左2次右1次,1次定焦点,符号定开口,开口内是焦点。(2)数量关系:4倍,相反数
这是一个没有标准答案的设计,学生可以自主联想发挥,创造性地理解抛物线四种形式。课堂上,每位同学都有话可说,有话要说,积极参与课堂,学习数学的兴趣被充分调动。课堂练习环节中,同学们都可以快速准确的回答出抛物线的方程、焦点和准线。
案例2.在《四种命题间的相互关系》一节中,学生曾经提出过这样一个问题:命题“若α是第二象限角,则错误!未找到引用源。 一定是第一象限角。”的否命题是什么?我并没有直接回答学生的问题,而是将问题又抛给了学生,让学生充分表达自己的想法。有的学生认为否命题是“若α不是第二象限角,则错误!未找到引用源。不一定是第一象限角”,有的学生则认为否命题是“若α不是第二象限角,则 错误!未找到引用源。一定不是第一象限角”。同学们的主要焦点在于“不一定是”还是“一定不是”,课上我没有急于完成课堂内容,也没有参与学生的讨论,而是给予学生充分的时间和空间让全班讨论辨析,最后辨明问题的关键。
争议是最好的老师,学生的思维一直在飞舞跳跃着,他们彼此间的思维碰撞胜过教师的千言万语。一节高效、精彩的课常常不是教师设计出来的,而是教师抓住某个稍纵即逝的瞬间,将问题进行升华,激发了学生创造灵感后的产物。
总之,“创造”环节是在“问题”、“发散”、“收敛”、 “综合”之后对整节课的升华和提高,是前四个环节的延续和发展,在整节课中占有不可替代的作用,需要教师用心设计和耐心指导,较好地体现“创造”环节在实施有效教学中的价值。
图分类号:G623.6A
1673-4564(2015)06-0165-03
2015—10—22
