矿山尾矿沉降特性及流变学特性分析
2015-08-23郭亚兵
杨 娟, 郭亚兵
(太原科技大学 环境与安全学院,山西 太原 030024)
矿山尾矿沉降特性及流变学特性分析
杨 娟, 郭亚兵
(太原科技大学 环境与安全学院,山西 太原 030024)
分别进行沉降实验和流变学实验,以便更好地了解尾矿的沉降特性及其流变学特性,进而得到尾矿的沉降规律以及尾矿屈服应力与其固体浓度的关系,并利用数值拟合得到固体浓度和屈服应力的自定义模型。结果表明尾矿沉降的初始阶段,其沉降速度较大,沉降明显,尾矿的屈服应力随着固体浓度的增加而增大。
尾矿;沉降特性;屈服应力;流变学
0 引言
浓缩机是固液分离过程的重要的设备,在各种工业领域得到了越来越广泛的应用。随着淡水资源日益减少及生态保护的要求日益严格,对废水的回收及固体废物的堆放成为世界各国高度重视的问题。因此,对浓缩机溢流水的水质及底流固体浓度的要求越来越高。为了满足日益提高的处理要求,必须对浓缩机进行科学的设计保证浓缩机的工艺性能。浓缩机的工艺性能与所处理的物料息息相关,提高浓缩机工艺性能的关键就是要了解所处理物料的特性,包括固体粒度、固体密度、固体絮凝性、固体表面化学性能及浆液的粘度、屈服应力等流变学参数。
随着计算流体力学(CFD)在固液分离及废水处理中的应用,全世界固液分离研究人员开始将计算流体力学(CFD)应用于浓缩机工艺设计优化中,利用CFD商业软件如3D-FLOW、ANSYS等进行浓缩机沉降- 浓缩过程的数值模拟。Frost et al.(1993)利用一个三维的CFD对废水在圆形平底浓缩机的流态进行了模拟仿真,并描述了耙架的刮刀角度和尺寸对输送效率的影响[1]。Rudman et al. (2008)利用CFD模型研究了小型浓缩机的耙架输送沉淀固体的状态及耙架所受的扭矩,并发现影响扭矩的两个主要因素是在行进方向的耙架的投影面积以及所移动的物料的屈服应力[2]。Mohanarangam and Stephens (2009)建立了一个三维的CFD模型,这个模型结合了二次沉淀池中的沉淀过程及上浮过程[3]。但是,这些分析并没有包含沉降- 浓缩工艺过程中对其影响较大的特定的工艺过程,如絮凝沉降模型、压缩沉降模型等;这些模型需要建立用户自定义模型,与CFD模型集成计算,才能得到较为实际的结果。
综上所述,对所处理的固体物料进行理化特性分析及流变学特性分析至关重要。本文利用XRD对样品进行了物相分析,利用激光粒度仪进行了粒度分析。在此基础上,进行了样品的絮凝沉降实验;按照Bingham模型、Herschel-Bulkly模型、Casson模型对底流浆液进行了流变学实验分析。根据实验数据,利用数值拟合技术获得了底流固体浓度与屈服应力自定义模型。这样可真实地反映底流浆液的流变学特性,为CFD仿真分析提供可靠的数据。
1 沉降理论及流变学理论
1.1 沉降基本概念及现象描述
在沉降柱中,除了固体和液体之间的密度差[4]之外,其中的悬浮液颗粒还会受到自身重力的作用,发生沉降现象,所以沉降柱内的悬浮液会自动分为澄清液层和浓浆层,从而实现其固液分离。
开始沉降前,将沉降柱中的悬浮液搅拌均匀,使整个沉降柱中的固体浓度分布是相同的。沉降过程开始后,沉降柱中的固体颗粒以相同的速度沉降,经过一段时间后,在沉降柱中会出现四个区域:清水区位于容器顶部、依次往下是等浓度区、过渡区和压缩区。随着沉降过程的进行,可以观察到,清水区与等浓度区之间形成了一个明显的交界面,而交界面的下沉速度可以代表颗粒的平均沉降速度。同时,在底部的压缩区,从压缩区的上表面起一直到管底,固体颗粒的沉降速度是逐渐减小的,到管底颗粒的沉降速度降为零,而且这一区域内悬浮固体会随着其下沉过程被逐渐压实。[5]
1.2 流变学理论
流变学的研究对象是流体,通常依据在一定的温度和剪切应力作用下流体所表现出的特性,把流体划分为牛顿流体和非牛顿流体两大类。尾矿膏体作为一种典型的非牛顿流体,对于其流变学特性的研究主要分析尾矿的屈服应力特性。流体的屈服应力是指对于某些非牛顿流体,施加的剪切应力较小时流体只发生变形,不产生流动。当剪切应力增大到某一定值时流体才开始流动,此时的剪切应力为该流体的屈服应力。
由于非牛顿流体的流变特性具有一定的复杂性,在研究过程中逐渐形成了一些不同的描述非牛顿流体流变学参数之间关系的流变模型,如Ostwald de Vaele模型,Bingham模型,Herschel-Bulkly模型,Carreau模型,Casson模型,Cross模型等。本次实验采用以下三种模型来研究尾矿的屈服应力特性。
(1)Bingham模型
Bingham模型是两参数模型中最常使用的,它的表达式见公式(1):
τ=τ0+μ0γ
(1)
式中τ—剪切应力,Pa;τ0—屈服应力,Pa;μ0—Bingham粘度,Pa·s;γ—剪切速率,s-1。
其中,剪切速率并不会影响到Bingham粘度,而且Bingham模型在高剪切速率时更适用,[6]Bingham模型为非牛顿流体的流变学模拟提供了最合适的流变参数τ0和μ0。
(2)Herschel-Bulkly模型
Herschel-Bulkly模型是最常用的三参数模型之一,其表达式见公式(2):
τ=τ0+Kγn
(2)
式中τ—剪切应力,Pa;τ0—屈服应力,Pa;K—粘度系数,Pa·sn;γ—剪切速率,s-1;n—流变特性指数[6]。
(3)Casson模型
Casson模型适用于存在屈服应力的非牛顿流体,其表达式见公式(3):
(3)
式中τ—剪切应力,Pa;τ0—屈服应力,Pa;γ—剪切速率,s-1;μ*—常数,Pa·s。
2 实验材料及实验过程
2.1 实验材料和设备
实验样品采用氧化铝尾矿,其比重为2.33g/mL,所用的絮凝剂为MF919。沉降实验使用2L的量筒,流变学实验使用型号为HAAKEVT550的粘度计,并采用PL100叶片转子以及其他的辅助工具。
(1)尾矿的物料分析
对所采用的尾矿物料进行XRD物相分析,可知尾矿样品中主要含有Al(OH)3,Fe2O3以及SiO2,具体成分分析如图1所示。
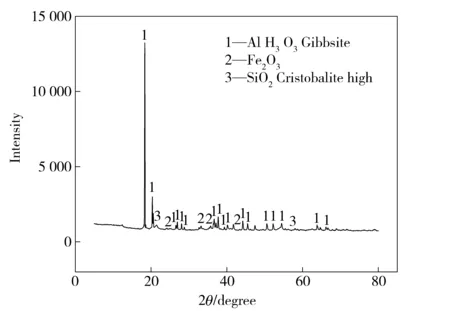
图1 尾矿物料成分分析图
(2)尾矿的粒度分析
利用Bettersize2000激光粒度分布仪对尾矿进行粒度分布实验,样品的粒径分布曲线如图2所示:
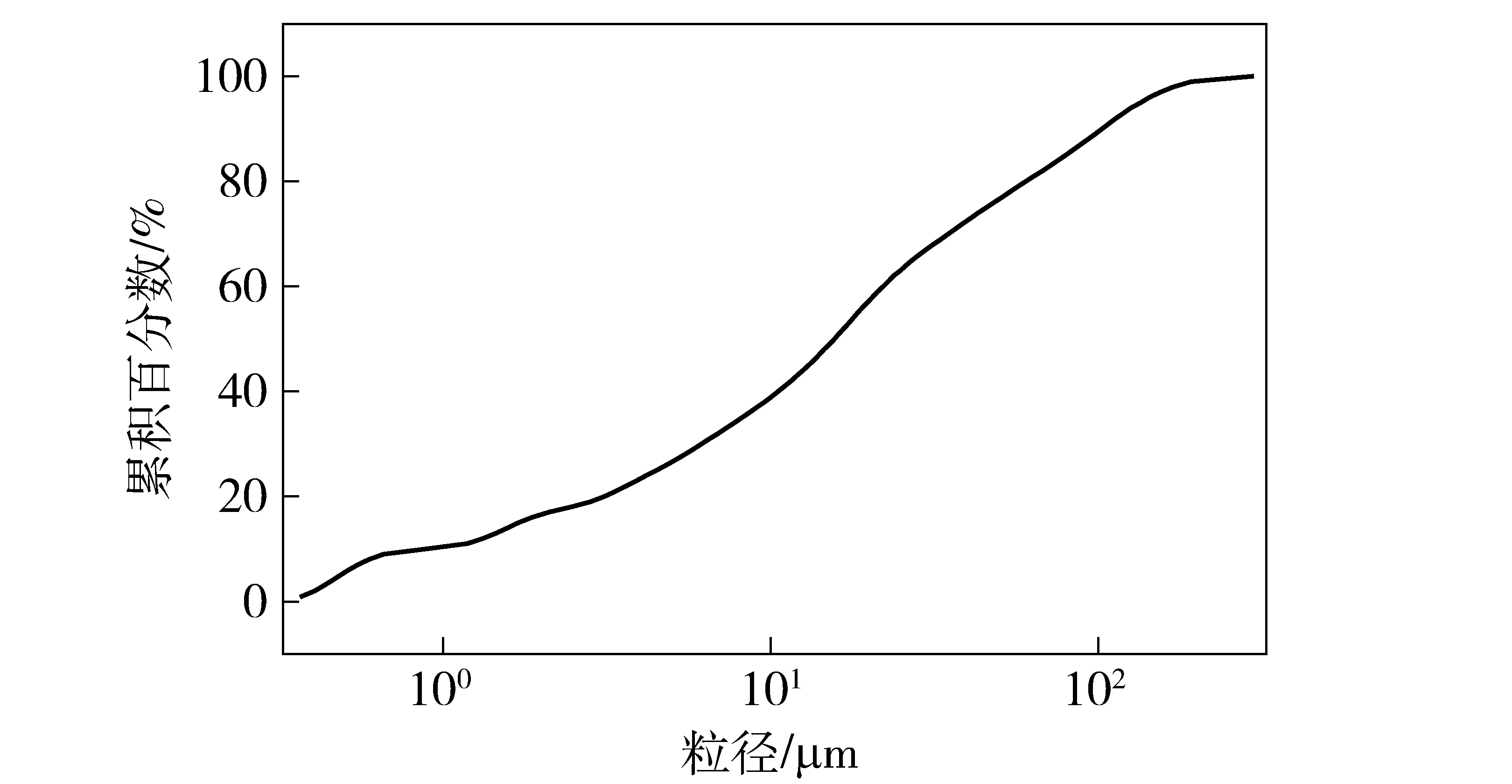
图2 粒度分布情况
2.2 实验过程
(1)沉降实验
称取210g尾矿样品于2L的量筒中,加水配制成为质量浓度为10%的浆液,使用搅拌器,对量筒内的矿浆进行搅拌,使之保持浓度均匀,加入8.5mL的高分子絮凝剂MF919继续进行搅拌,使矿浆与絮凝剂进行充分均匀的接触。停止搅拌的同时开始计时,并在一定时刻读取沉降液面的高度并记录。待液面高度不再发生变化,则静态沉降实验完成。
(2)流变学实验
称取635g的尾矿样品于6L大容器中,加水配置成质量浓度为10%的浆液,并加入25.5mL剂量的高分子絮凝剂MF919进行充分的搅拌,使固体颗粒与絮凝剂充分接触,完成絮凝反应。待反应充分进行,静置24小时后倒去上清液,得到满足粘度计测试实验所需浓度的污泥样品。
粘度计实验前称取少量污泥样品于容器中,测得污泥样品的初始固体浓度为73.76%,实验过程中,对样品进行不断稀释得到不同浓度的样品进行测量。
利用HAAKVT550粘度计测定污泥样品的流变学参数。分别对不同浓度的样品进行测量,并利用Rheo Win软件对所得数据进行处理得到所需要的结果。
2.3 实验结果与分析
2.3.1 沉降实验结果与分析
记录沉降实验数据,整理可以得到沉降时间与界面高度读数的关系曲线如图3所示:
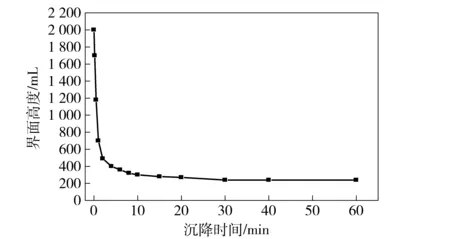
图3 沉降时间与界面高度关系曲线
实验结果表明:静态沉降过程在实验开始的最初10min内比较显著,沉降速度大,界面高度变化明显。在后续沉降过程中沉降速度逐渐变小,主要表现为压实现象。
2.3.2 结果与分析
实验共有七组样品,样品的浓度分别为:73.8%,72.7%,71.6%,70.5%,69.5%,68.5%,67.6%。分别利用HAAKVT550粘度计进行屈服应力的测点,并用不同的模型进行数据的处理,可以得到不同浓度时对应的屈服应力,并进行数值拟合从而建立不同模型下屈服应力与固体浓度之间的关系曲线。
分别利用Bingham模型,Herschel-Bulkly模型,Casson模型进行数据处理,可得到不同浓度样品的屈服应力曲线如图4所示:
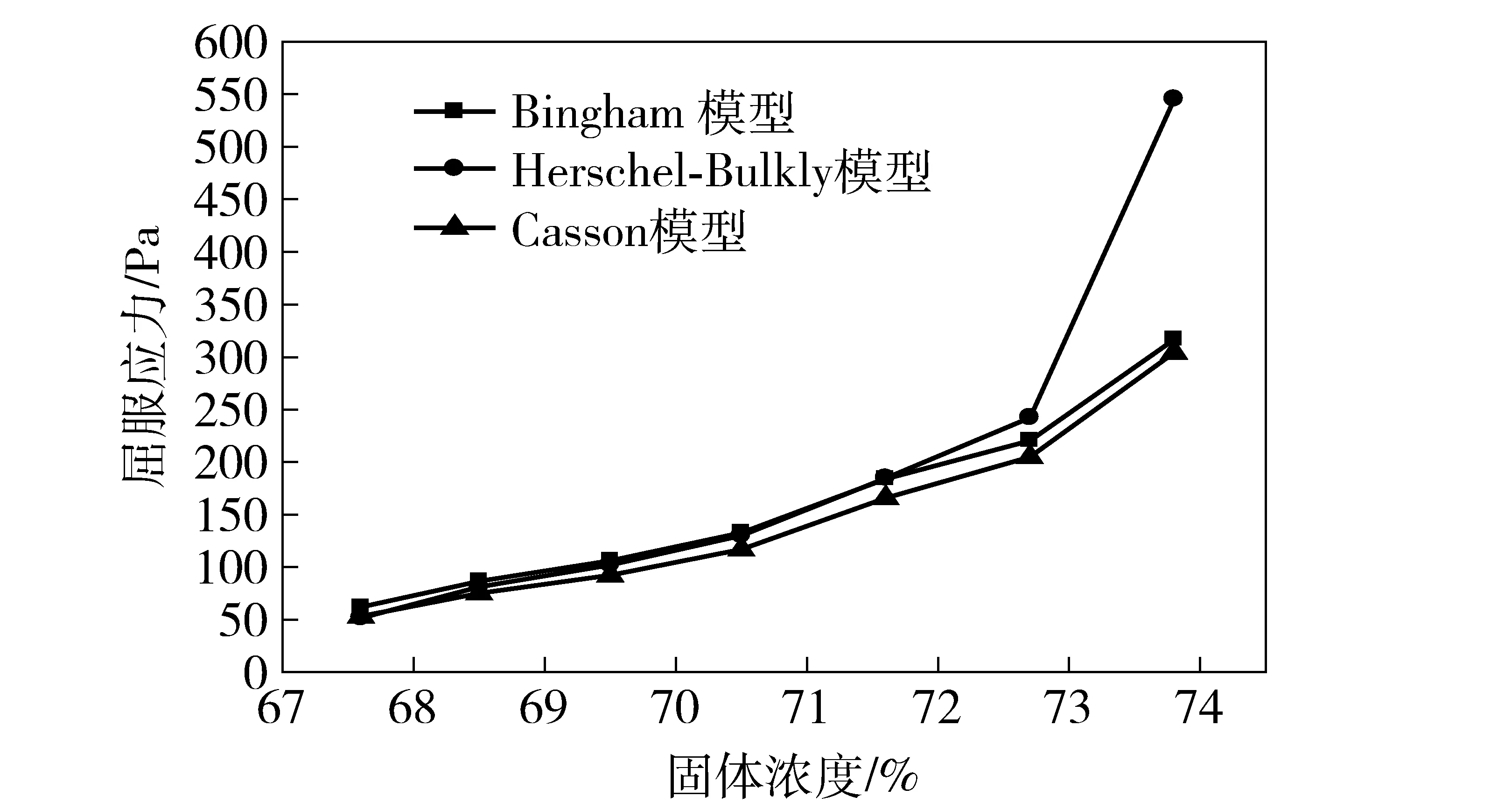
图4 处理结果
对上述数据进行数值拟合,由于屈服应力会随着固体浓度的增加呈指数型增长[8],所以选用指数函数进行曲线拟合,可得到三种不同模型下的屈服应力与固体浓度之间的关系曲线。所采用的拟合公式为:f(x)=a×exp(b×x),得到满足Bingham模型的a=2.433×10-6,b=0.2529,拟合度R-square为0.992 9,满足Herschel-Bulkly模型的a=2.088×10-12,b=0.449,拟合度R-square为0.949 7,满足Casson模型的a=4.136×10-7,b=0.276 3,拟合度R-square为0.991 7。数值拟合得到的关系曲线如图5所示:
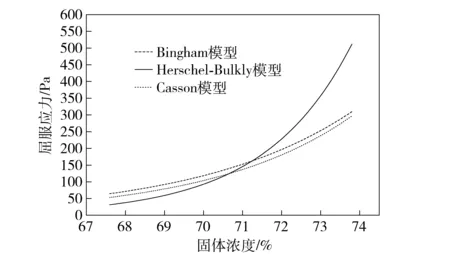
图5 应力与固体浓度关系曲线
通过以上数据及拟合屈服应力与固体浓度的关系曲线,可以得出以下结果:
(1)加入絮凝剂的尾矿样品,存在明显的屈服应力。
(2)样品随着固体浓度的增加,屈服应力不断增大。这是因为随着固体浓度的增加,流体中的颗粒数目增加导致其流动阻力增大,所以尾矿的剪切粘度也会增大,相对应的屈服应力也就变大[9]。
(3)对于所用的尾矿样品,利用不同的模型进行数据的处理分析得到的屈服应力并不完全相同。在固体浓度低时三种模型所得到的屈服应力值相近,而高浓度时Bingham模型与Casson模型的屈服应力值相近。
3 结论
沉降实验的进行可以得知,加入了絮凝剂的尾矿样品具有很明显的沉降特性,能够短时间内完成沉降过程,进入到压实阶段。
尾矿样品的屈服应力随着固体浓度的增加而增大,并且满足指数型增长关系。同时,相同函数对于
不同模型的拟合也是有差别的,在实际应用中,需要选择更加符合实际工业情况的模型来进行生产操作。
尾矿样品的沉降特性和流变学特性对于尾矿的后续处理与处置有着相当重要的意义。尾矿样品的沉降特性还会受到絮凝剂种类的影响,其流变学特性除与固体浓度有关系,还与剪切速率、温度、组成成分、粒径等因素有关系,这些都有待于进一步的探讨与研究。
[1] Frost R,Halliday J, Dee A. Continuous consolidation of sludge in large scale gravity thickeners [J]. Water Science & Technology, 1993(28):77-86.
[2] Rudman M, Simic K,Paterson D,et al. Raking in gravity thickeners[J]. International Journal of Mineral Processing, 2008(86): 114-130.
[3] Mohanarangam K,Stephens D. CFD modelling of floating and settling phases in settling tanks[R]. 2009.
[4] Rushton,A,Ward,A S, Holdich,R G. 固液两相过滤及分离技术[M]. 北京:化学工业出版社,2005:6.
[5] 郭亚兵,胡钰贤,王守信. 沉降- 浓缩理论及数学模型[M]. 北京:化学工业出版社,2014:64-66.
[6] 曹秀芹,崔伟莎,王洪臣,等. 污泥流变特性及其变化规律的研究进展[J]. 环境工程, 2014,32(10):9-12.
[7] 喻有理,王小力. 毛细管粘度计测casson流体流变特性方法研究[J]. 物理与工程, 2000(5):24-25.
[8] 吴爱祥,焦华喆,王洪江,等. 膏体尾矿屈服应力检测及其优化[J]. 中南大学学报, 2013,44(8):3370-3376.
[9] 王丽华,徐继润. 絮凝污泥悬浮液流变性质研究[J]. 流体机械, 2007,35(6):1-4.
Analysis of Settling Characteristics and Rheological Characteristics of Mine Tailings
YANG Juan, GUO Ya-bing
To understand the settlement characteristics and rheological properties of tailings better, sedimentation experiments and rheological experiments are carried out. We can obtain the law of tailings settlement and the relationship between the yield stress of tailing and its solid concentration, and get a custom model of solid concentration and yield stress by using numerical fitting technology. Results show that the initial stage of tailings deposition sedimentation velocity is larger and the subsidence is obvious, the yield stress increases with the increasing of tailings solid concentration.
tailings;settlement characteristics;yield stress;rheology
2015-09-06
山西省科技攻关项目(20130313006-1);山西省特色、重点学科建设项目(201214505)
杨 娟(1990-),女,山西晋中人,在读研究生,研究方向为尾矿处理模拟仿真。
TD982
A
1003-8884(2015)06-0009-04
