一种基于BP神经网络改进算法的PM2.5预测方法
2015-08-22孙荣基张小琴李洪鲁盛利伟冯裕钊
孙荣基,赵 松,张小琴,李洪鲁,盛利伟,冯裕钊
(1.后勤工程学院 建筑规划与环境工程系,重庆 401311,2.69068部队,新疆 830000,3.国家救灾应急装备工程技术研究中心,重庆,401311)
· 环境监测 ·
一种基于BP神经网络改进算法的PM2.5预测方法
孙荣基1,赵松2,张小琴3,李洪鲁1,盛利伟1,冯裕钊1
(1.后勤工程学院 建筑规划与环境工程系,重庆401311,2.69068部队,新疆830000,3.国家救灾应急装备工程技术研究中心,重庆,401311)
针对BP神经网络进行空气污染预测收敛速度过慢和学习过程中易出现“过适配”的问题,提出了利用主成分分析和提前终止训练法对传统BP模型进行改进的新算法。并利用MATLAB平台进行了仿真研究,结果表明:改进后的算法提高了BP神经网络的预测精度和泛化能力,能较好地实现PM2.5浓度预测。
PM2.5; 空气污染预测; BP神经网络; 主成分分析; 提前终止法
PM2.5指环境空气中动力学当量直径小于或等于2.5微米的颗粒物。PM2.5在大气中的含量很少,与较粗的大气颗粒物相比,粒径小,面积大,活性强,易附带有毒、有害物质(例如,重金属、有机物、微生物等),且在大气中的停留时间长、输送距离远,可直接进入人体肺部,因而对大气环境质量和人体健康的影响更大,因此,PM2.5引起了人们的广泛关注。空气中污染物浓度是由污染源、气象条件、下垫面、理化生过程的耦合等多种因素共同作用的结果,具有很强的非线性特征[1],传统的预测方法难以取得令人满意的效果。
BP(Back Propagation)神经网络是误差反向传播的多层前馈型人工神经网络,具有极强的非线性映射能力[2],在函数逼近、模式识别、智能控制等众多领域都有着广泛的应用[3]。BP神经网络在空气污染预测中的应用主要集中在污染物浓度的短期预测和污染指数预测两个方面。Sang等[4]利用BP网络模型预测汉城大气中臭氧浓度,设计了由30个输入节点、50个隐含层节点和6个输出节点组成的单隐含层BP神经网络,实现了汉城臭氧浓度时空分布的精确预报。Sofuoglu[5]采用BP网络预测空气污染物浓度,结果表明该模型具有较高的预测精度。郭庆春等[6]建立了基于BP 神经网络的空气污染指数非线性时间序列预报模型用于预测宝鸡市空气污染指数,仿真结果表明:该模型泛化能力强,精确度高,能较好地预测宝鸡市日空气污染指数。Mok[7]采用BP网络对澳门短期SO2的浓度进行预测,两个模型的误差分别为13.71%和14.45%,仿真试验表明:即使在训练数据十分有限的情况下,BP神经网络仍具有较高的预测精度。赵慧宏[8]等对兰州市1995~2000年工业SO2排放总量的分析表明: SO2年排放总量具有很强的非线性特征,并基于MATLAB 平台构建了BP网络模型,仿真结果较为理想。王俭等[9]对传统的BP神经网络算法进行了改进,使用遗传算法优化网络结构,利用加动量项和变步长的方法提高BP神经网络的收敛速率。王灿星[10]建立的BP神经网络以湿度、温度、气压、雨量、风速等气象数据为网络的输入因子,以杭州市1999~2001年TSP(Total Suspended Particulate)作为BP网络的样本数据,模型均方差小于0.2%。杨树平等[11]根据环境部门和气象部门提供的数据分别建立了用于预测NO2,SO2和PM10浓度的BP神经网络,网络的输入节点数、隐含层节点数、输出节点数分别为10、5、1, 仿真试验结果表明:NO2、SO2、PM10平均绝对误差分别为0.004、0.006、0.009。
1 主成分分析和提前终止算法
1.1主成分分析
我们经常会遇到研究多个变量的问题,如果能把多个变量简化为少数几个既能代表原始变量绝大多数信息又互不相关的变量,这样就能把复杂问题简单化。主成分分析是将多个变量简化为少数几个互不相关的综合变量的统计分析方法,是一种数学降维方法。主成分分析的数学模型如下:
对于一个样本集,观测 p个变量x1,x2,…,xp,n个样本的样本资料矩阵为:
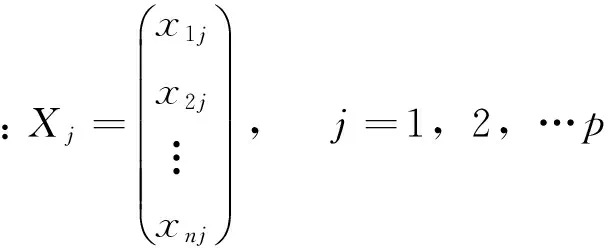
主成分分析就是将多个观测变量综合成为少数新的变量(综合变量),即
(1)
简化为:
Fj=aj1x1+aj2x2+…+ajpxp,j=1,2,…,p(2)
并且要求满足以下条件:
Fi,Fj互不相关(i≠j,i,j=1,2,…p);
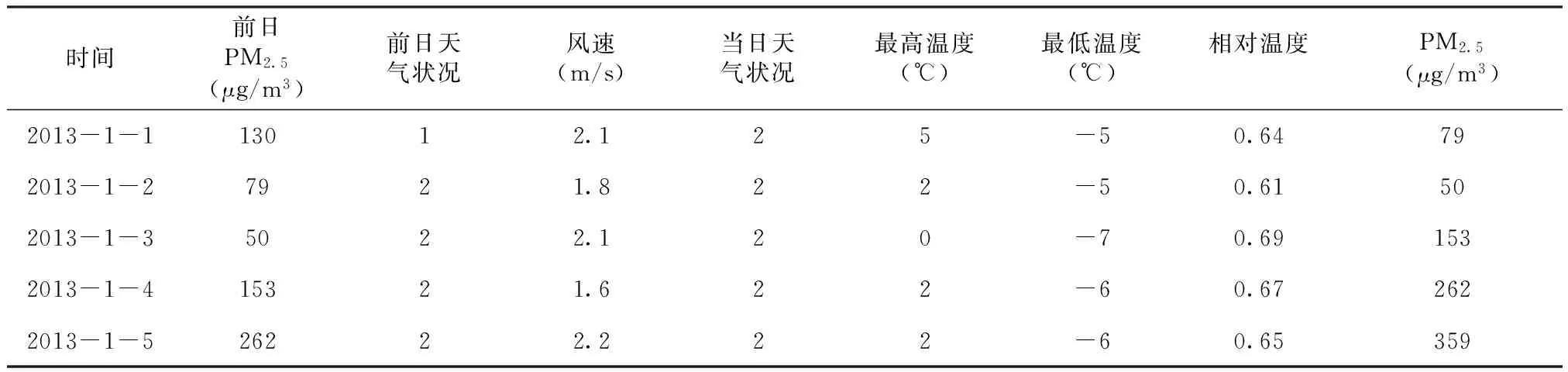
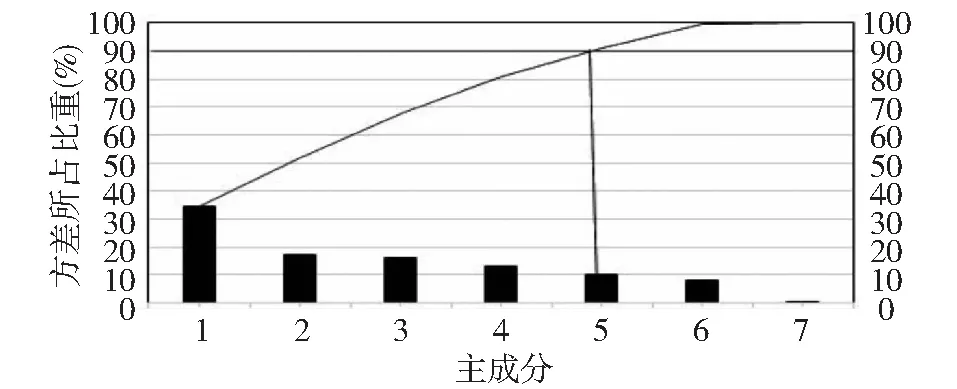
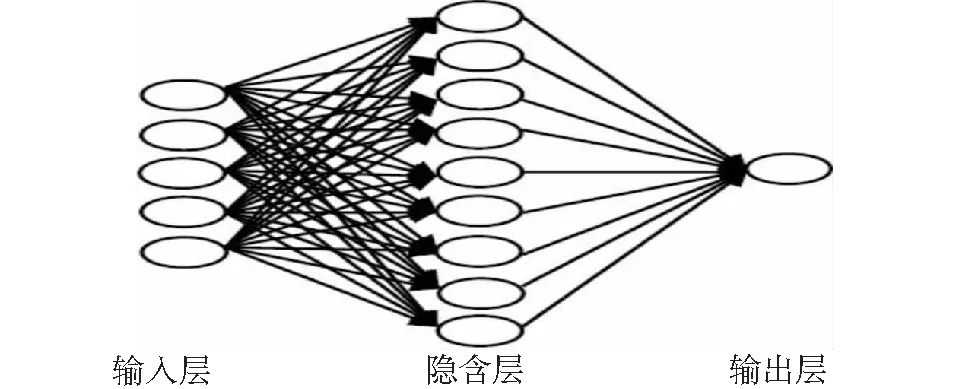
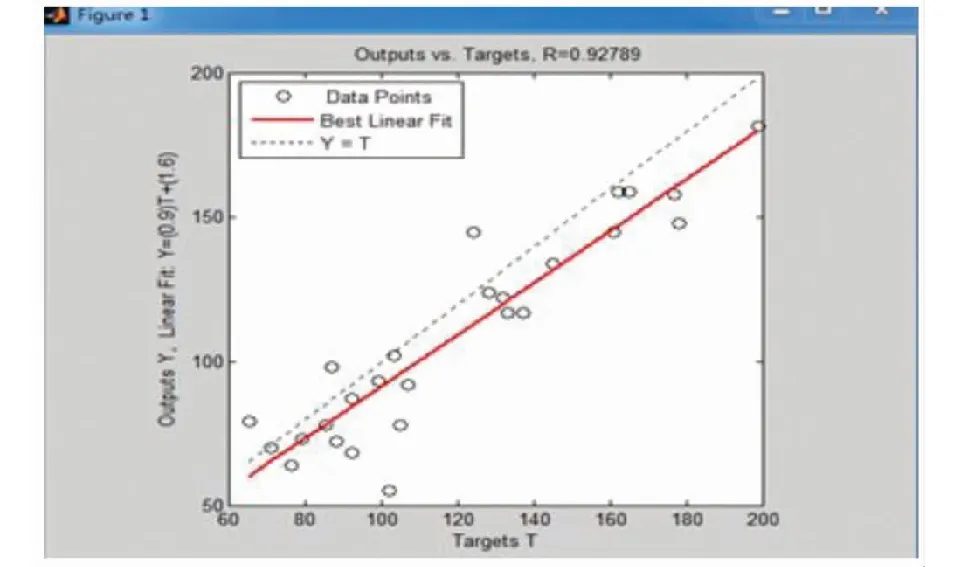
Fi的方差大于Fj的方差(i 其中,Fj称为第j个主成分,aij称为主成分系数。 1.2提前终止算法 泛化能力是指已经训练好的网络对未知样本是否具有良好的预测性能[12],是评价神经网络性能优劣的重要指标之一,缺少泛化能力的网络是没有实际应用意义的[13]。提前终止法能很好地提高BP神经网络的泛化能力。 在提前终止算法中,样本数据被分为3个子集,分别是训练样本集、验证样本集和测试样本集。验证样本的选择十分重要,应该包含训练样本集的所有特征。已有的研究表明[14,15],网络训练存在一个最佳训练次数,在达到该训练次数前,随着训练次数的增加,训练集和验证集误差同时下降;当超过该训练次数,训练集误差继续减小而验证集误差开始增加。在达到最佳训练次数之前停止训练则训练不足,在达到最佳训练次数之后继续训练则训练过度。提前终止法是指为了提高网络模型的泛化能力,当训练次数达到最佳训练次数则停止训练的方法。 2.1算法改进的基本思路 本文提出了一种改善BP神经网络的预测性能算法:一是针对收敛速度过慢的问题,采用主成分分析方法对训练样本进行处理;二是针对训练中“过适配”的问题,采用提前终止法进行网络训练。 传统BP算法会对样本数据进行归一化处理,这种方法可以把训练样本限定在一个较小的范围内,但是它并不能减少样本维数,因此,在样本维数较多的情况下,这种方法对于提高网络收敛速率没有明显的效果[16]。本文采用主成分分析法对训练样本进行处理,降低样本维数和去除冗余信息。而针对网络训练“过适配”的问题,本文采用提前终止法进行网络训练。根据训练样本集与验证样本集误差的变化情况,确定网络模型的最佳训练次数,当训练次数达到最佳训练次数后则停止训练,以提高网络泛化能力。算法改进的基本思路是:利用主成分分析法对样本进行预处理,将处理后得到的主成分样本代替原始样本作为神经网络的输入样本,再使用提前停止法对网络进行训练,达到最佳训练次数后停止训练。 2.2改进算法的流程 Step.1:采用主成分分析法对初始样本进行处理,计算相关系数矩阵及特征向量和特征值。 相关系数矩阵R: (3) 根据特征方程,计算特征值λi和对应的特征向量ei。 Step.2:计算各成分的贡献率和累计贡献率,并取累计贡献率达到85%~95%成分组成新样本以代替原始样本。 第i个主成分贡献率计算公式: (4) 前k个主成分贡献计算公式: (5) Step.4:设置BP神经网络相关参数,计算隐含层节点个数,确定神经网络模型结构; Step.5:将训练样本和验证样本输入到网络中,分别对具有不同隐层节点数的神经网络采用提前终止法对网络进行训练。 Step.6:以预测精度为评价标准,确定最佳网络模型结构; Step.7:根据最佳网络模型期望输出与实际输出之间的误差进行网络性能评价。 实验利用改进算法对西安市PM2.5浓度预测,以检验其预测性能。实验数据为西安市2013年1月1日~2013年4月27日的PM2.5日平均浓度和部分气象条件。根据经验和查阅相关资料,确定当日PM2.5浓度的影响因素主要有以下7个方面:前日PM2.5浓度、前日天气状况、风速、相对湿度、最高温度、最低温度和当日天气状况。部分样本数据如1所示。 表1 部分样本数据 注:天气状况一栏中分别用1、2、3表晴、阴(多云)、雨(雪)。 本文采用统计学R软件对样本数据进行主成分分析,分析结果如表2和图1所示。 表2 主成分分析结果 图1 主成分比例Fig.1 The proportion of Principal component 由表2和图1可知,按方差贡献率大小排序依次为:前日PM2.5浓度、前日天气状况、风速、当日天气状况、最高温度、最低温度和相对湿度,并且前5项的累积方差贡献率达到91%以上。因此,本文选取前5项组成新样本作为神经网络的输入因子。由主成分分析确定了新样本集,并按上文所述方法对新样本数据进行分组。 采用MATLAB平台进行仿真实验。根据Kolmogorov[17]定理,具有单隐含层(隐含层节点数足够多)的BP神经网络能在闭集上以任意精度逼近任意非线性连续函数。因此,本文采用单隐层BP神经网络,并根据实际需要确定网络模型的相关参数:输入层节点数为5,输出层节点数为1,设定网络的误差目标为goal=0.01, 学习效率lr=0.01。隐含层节点数按公式(6)计算。 (6) 式中,k表示隐含层节点数; m表示输入层节点数; n表示输出层节点数; a表示[1,10]之间的整数。 由公式(6)可知,本实验中BP神经网络最佳隐含层节点数应在4~12之间。分别对隐含层节点数不同的BP神经网络进行训练和预测,其结果如表3所示。由表3知,在隐含层节点数较少的情况下,预测精度随着节点数的增加而上升,当节点数为9时,网络的预测精度达到最高,当节点数大于9之后,预测精度开始下降。这说明,BP神经网络的隐含层节点数并不是越多越好,要根据研究问题的复杂程度及样本数据的特点,确定最优的隐含层节点个数。 表3 不同隐含层节点数BP神经网络的预测精度 基于以上分析,本文选取的隐含层节点数为9,本文最终采用的BP网络模型如图2所示。并分别对改进后算法和传统算法进行了仿真试验,实验结果如图3和图4(输入层节点数为7,隐含层节点数为9单隐含层的传统BP神经网络测试误差网线图)所示。传统BP神经网络的预测精度只有53%,而改进后的网络预测的准确精度达到了92%;传统BP神经网络在训练中迭代至352步才停止,而改进后的算法迭代至38停止训练,这是因为此时验证集误差开始增大。因此,改进后的BP神经网络算法不仅大大提高了网络的收敛速度,同时也提高了网络的预测精度,具有更强的泛化能力。 图2 本文采用的BP网络模型Fig.2 The BP network model in this paper 图3 改进后算法的测试误差曲线Fig.3 The error curve of the improved algorithm 利用2013年4月17日~2013年4月26日数据进行预测误差分析,分析结果如表4所示。实际值为xreal,预测值为xfore,绝对误差为Eerror,相对误差为Eper,平均误差为Eaver,方差为Esq计算的公式为: 图4 传统BP神经网络测试误差曲线Fig.4 Test error curve of conventional BP neural network Eerror=|Xfore-Xreal| 表4 数据误差分析 本文利用主成分分析和提前终止算法对传统BP神经网络算法进行了改进,先采用主成分分析法对高维初始样本进行预处理以形成低维的新样本,达到了降维去噪、剔除冗余信息的目的,再采用提前终止法对网络进行训练,克服了网络训练“过适配”的问题,增强了网络的推广能力。通过实验分析,这种方法加快了网络的收敛速率,提高了网络的预测精度,强化了网络的泛化能力,为BP神经网络在空气污染预测中的应用提供了一条新思路。 [1]RAGA G B, MOYNE. On the nature of air pollution dynamics in Mexico City. Nonlinear analysis [J]. Atmos Environ, 1996, 30(23): 3987- 3993. [2]张德丰. MATLAB神经网络编程[M].北京:化学工业出版社,2011.133-135. [3]谢文兰. 对提高BP神经网络泛化能力的分析和总结[J].广东科技, 2011,(7):72-73. [4]Sang Hyun John. Prediction of Ozone Formation Based on Neural Network[J]. Energy, ASCE, 2000,8:688-696. [5]刘道文,忽海娜.非线性时间序列混沌特性分析及短期预测[J].计算机仿真,2012, 29(10):370-373. [6]郭庆春,等. 人工神经网络在大气污染预测中的应用研究[J]. 工业仪表与自动化装置,2012,(4):18-22. [7]Mok K M, Tam S C. Short-term prediction of SO2concentration in Macau with artificial neural networks [J].Energy and Buildings,1998,(28):279-286. [8]赵慧宏. 兰州市SO2排放总量预测的BP 人工神经网络模型[J].甘肃环境研究与监测, 2001,14(3): 157-159. [9]王俭, 胡筱敏, 郑龙熙, 等. BP模型的改进及其在大气污染预报中的应用[J]. 城市环境与城市生态, 2002,15(5):17-19. [10]王灿星, 祁国伟,何曦. BP神经网络用于大气中颗粒物(TSP)预测的研究[J].仪器仪表学报, 2003, 24(增刊):529-530. [11]杨树平, 冯晖, 黄晓.BP 神经网络在环境空气质量预报中的应用[J]. 云南环境科学, 2003,(22):52-54. [12]雷蓓. 人工神经网络在大气污染预报中的应用研究[D].北京:北京工业大学,2007. [13]武妍, 张立明. 神经网络的泛化能力与结构优化算法研究[J]. 计算机应用研究, 2002,(6):21-25. [14]周品. MATLAB神经网络设计与应用[M].北京:清华大学出版社,2013.180-183. [15]韩力群.人工神经网络理论、设计及应用[M].北京: 化学工业出版社, 2004. [16]夏玫, 陈立潮, 王新波. 一种提高BP神经网络泛化能力的改进算法[J]. 计算机技术与发展, 2009,(9):62-65. [17]黄丽. BP神经网络算法改进及应用研究[D].重庆:重庆师范大学,2008. An Improved PM2.5Prediction Model based on BP Neural Network SUN Rong-ji1,ZHAO Song2,ZHANG Xiao-qin3,LI Hong-lu1,SHENG Li-wei1,FENG Yu-zhao1 (1.Dept.ofArchitecturePlanning&EnvironmentalEngineering,LEU,Chongqing401311,China;2.The69068TroopsofPLA,Xinjiang830000,China3.NationalDisasterReliefEmergencyEquipmentEngineeringTechnologyResearchCenter,Chongqing401311,China) Aimed at solving the problems of low convergence rate in the prediciton of the air pollution by BP neural network and the “over-adaptation” during study, this paper proposed a new algorithm, which used principle components analysis and early termination training method to improve conventional BP algorithm. Simulation study is carried out on the platform of MATLAB. The result showed that the improved algorithm could increase prediction accuracy and enhanced the generalization ability of BP neural network. Thus, it can better predict the concentration of PM2.5. PM2.5; air pollution prediction; BP neural network; principle components analysis;early termination 2015-04-15 孙荣基(1988- ),男,河南信阳人,中国人民解放军后勤工程学院环境科学与工程专业2013级在读硕士,研究方向军事环境监测与评价。 冯裕钊,1297345332@qq.com。 X513 A 1001-3644(2015)04-0085-06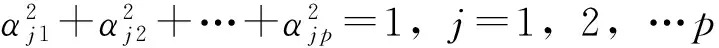
2 BP神经网络算法的改进
3 仿真实验分析




4 结 语
