基于MCMC模拟的MGPD模型及其在地质灾害风险度量中的应用

欧阳迪飞　杨扬　甘柳　李应求

摘 要 基于马尔科夫链蒙特卡洛（简记为MCMC）模拟的参数贝叶斯估计，对改进的广义帕累托分布（简记为MGPD）模型进行了优化，并利用该模型得到了地质灾害损失的在险损失值（简记为VaR）和条件损失值（简记为CVaR）.以湖南娄底市地质灾害损失数据进行实证分析及模型适应性检验，结果表明：优化后的模型不仅具有很好的极值数据描述能力，而且具有较强的适用性.

关键词 马尔科夫链蒙特卡洛模拟；贝叶斯估计；改进广义帕累托分布；地质灾害

中图分类号 O213.2 文献标识码 A

The MGPD Model Based on MCMC Simulation

and Its Application in Geological Disaster Risk Measure

OUYANG Difei1，YANG Yang1， GAN Liu2， LI Yingqiu1

（1.School of Mathematics and computing Science， Changsha University of Science

and Technology， Changsha，Hunan 410004，China；

2. School of treasury and finance， Hunan University of Commerce， Changsha， Hunan 410205，China）

Abstract We used Bayesian estimation based on Markov Chain simulation to optimize the meliorated Generalized Pareto Distribution model （MGPD）， and obtained the estimation of the Value at Risk（VaR） and Conditionl Value at Risk（CVaR）. The empirical study and adaptability test of the model were based on geological disasters loss data of Loudi City in Hunan Province. The conclusion shows the optimized model has not only excellent ability in describing the data， but also extensive applicability.

Key words Markov Chain Monte Carlo simulation； Bayesian estimation； meliorated generalized Pareto distribution model； geological disaster

1 引 言

地质灾害是指在地质作用下，地质自然环境恶化，造成人类生命财产损毁或人类赖以生存与发展的资源和环境发生严重破坏的过程或现象.据国土资源部统计，2013年，全国共发生各类地质灾害15403起，造成481人死亡、188人失踪、264人受伤，造成直接经济损失101.5亿元.死亡人数与上年相比，同比增加7.5%.地质灾害风险评估作为一项极具现实意义的重要研究课题和减轻灾害损失的非工程性重要措施，其研究成果已经引起了社会的广泛关注.这其中涉及一系列与统计理论相关的方法，通过对地质灾害风险进行评估及管理来刻画地质灾害风险，对政府及保险机构防范风险、稳定经营、降低破产概率就显得至关重要.

地质灾害风险导致索赔的统计数据数量不多、质量不高，因此在进行风险研究时采用传统的精算方法很难准确预测未来损失和管理风险.极值理论常用于研究随机变量，或一个随机过程的随机性质，最常见的是指在特殊情况下发生极端事件的概率.因此，在分析解决地质灾害风险等随机问题时，极值理论大有用武之地.极值统计中主要有两类模型，一类是区块极值模型（BlockMmaximum Model，简称为BMM），这种模型主要对组最大值建模.另一类是基于广义帕累托（Generalized Pareto）分布的模型（简称GPD模型），它是对观察值中所有超过某一阈值的数据建模.由于GPD模型充分利用了数据中的极值信息，因此针对地质灾害风险导致统计数据数量不多、质量不高的情况，采用GPD模型将更有用[1].

经 济 数 学第 32卷第2期

欧阳迪飞等：基于MCMC模拟的MGPD模型及其在地质灾害风险度量中的应用

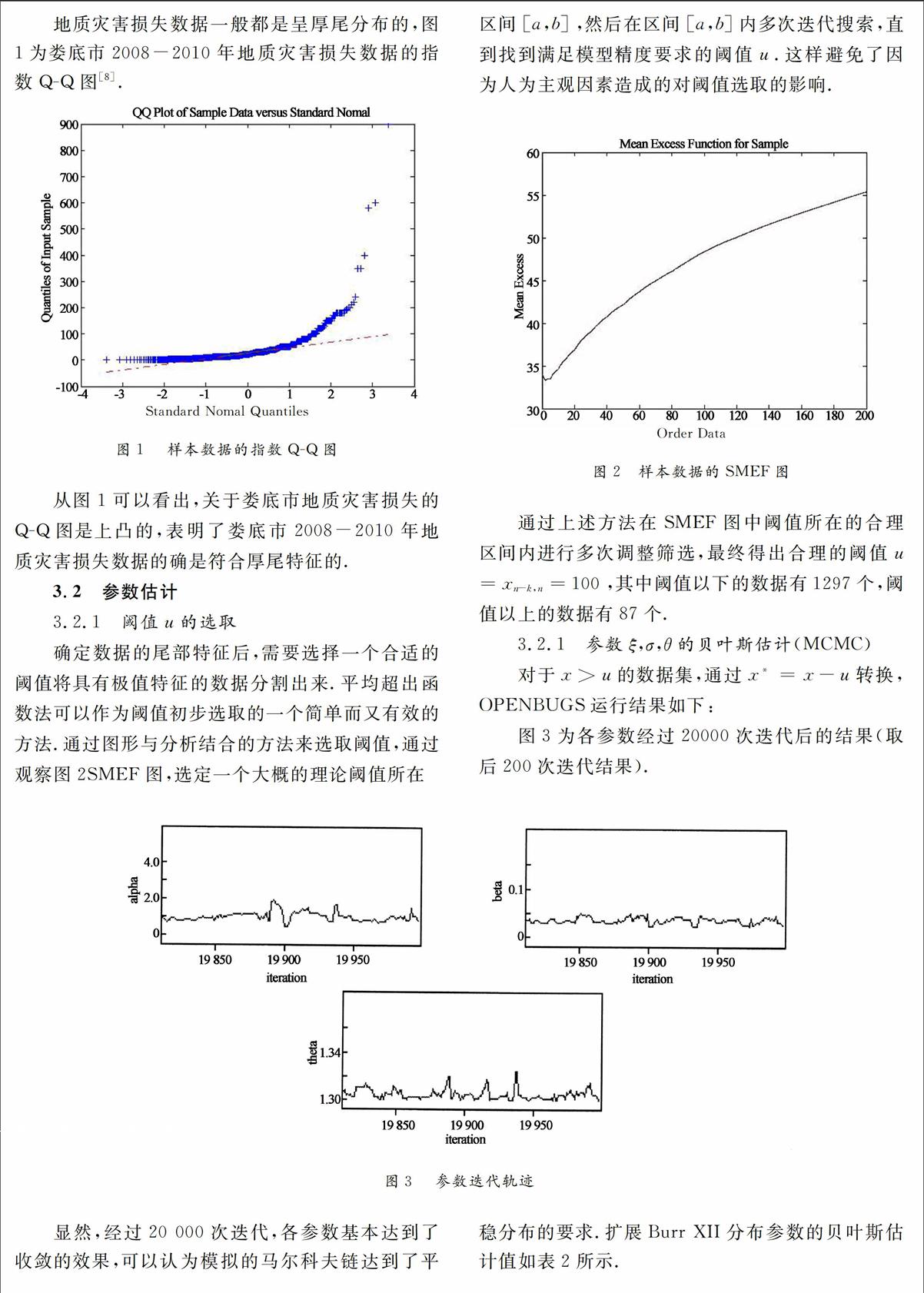
以湖南省娄底市地质灾害为例，利用MGPD实证得到了当地的地质灾害损失的在险风险值和条件在险风险值.首先，根据QQ图和经验平均超出函数图对原始数据进行诊断并选取阈值，结果显示样本数据具有厚尾的特征；其次，选择扩展Burr XII分布对这类数据进行描述，并基于MCMC贝叶斯估计确定分布函数中的参数估计值；最后，利用所得到的分布函数检验了模型的适应性以及测算了不同置信水平下的在险风险价值损失、条件在险风险价值损失，并据此说明了研究结论和实际意义.

2 MGPD模型

2.1 扩展Burr XII分布

MGPD模型将所有超出给定充分大阀值的观测值作为观测样本，进而研究观测值的渐进分布.MGPD模型基于扩展Burr XII分布.

4 结 论

首先，MGPD模型能很好地描述地质灾害损失数据，对尾部极值数据的捕获能力较高.其次，基于MCMC模拟的贝叶斯估计对模型的适应性具有较好地改善，能够保证一定程度下的数据波动不会对模型造成明显的干扰.其次，实证得出在99%置信水平下认为未来某一次的地质灾害在险风险损失为197.103万元，显然，为规避巨灾损失，我国势必需要加强对地质灾害的防治与预警力度.

地质灾害在中国乃至全世界都是一个无法回避的问题，如何有效地规避地质灾害风险，尽可能的降低地质灾害给国家、政府以及人民带来的影响是一个在很长时间内都需要面对的问题.一方面应该做好地质灾害的预防工作，避免因为相关设施的落后、反应机制的不健全，造成不必要的人员财产损失.另一方面，即在灾害发生之后，如何有效、高效地减轻地质灾害带来的负面影响，于国于民无疑是有重要意义的[10].显然，只有综合考虑这两个方面，才能防患于未然，我国有必要加快地质灾害防治体系的完善，尽可能降低地质灾害给国民经济和人民生活带来的不利影响.

参考文献

[1] 欧阳资生. 地质灾害损失分布拟合与风险度量[J]. 统计研究， 2012， 28（11）： 78-83.

[2] Shao Q， Wong H， Xia J， et al. Models for extremes using the extended threeparameter Burr XII system with application to flood frequency analysis[J]. Hydrological Sciences Journal， 2004， 49（4）： 685-702.

[3] 欧阳资生. 极值估计在金融保险中的应用[M]. 北京：中国经济出版社， 2006： 127-129.

[4] I USTA. Different estimation methods for the parameters of the extended Burr XII distribution[J]. Journal of Applied Statistics， 2013， 40（2）： 397-414.

[5] G MATTHYS， J BEIRLANT. Estimating the extreme value index and high quantiles with exponential regression models[J]. Statistica Sinica， 2003， 13（3）： 853-880.

[6] 刘睿， 詹原瑞， 刘家鹏. 基于贝叶斯MCMC的POT模型——低频高损的操作风险度量[J]. 管理科学， 2007， 20（3）： 76-83.

[7] 李应求， 田琴， 戴志锋. 基于鲁棒均值下半偏差模型的供电公司购电组合策略[J]. 经济数学， 2014， 31（4）： 14-19.

[8] 李应求， 甘柳， 魏民. 一类多险种复合PoissonGeometric过程风险模型研究[J]. 统计与决策， 2010 （7）： 53-55.

[9] 李应求， 刘薇， 陈文锋. 聚类分析视角下地区保险业发展差异研究—基于湖南省各地市的截面数据分析[J]. 时代金融， 2009（1）：117-119.

[10]李应求， 刘朝才， 彭朝晖. 不确定条件下企业的投资规模决策[J]. 运筹学学报， 2008， 12（2）： 121-128.