自泵送流体动压型机械密封性能分析
2015-08-20周敏孙见君马晨波於秋萍周培岩
周敏,孙见君,马晨波,於秋萍,周培岩
(南京林业大学机械电子工程学院,江苏 南京 210037)
引 言
目前,广泛应用于石油、化工、电力和冶金行业的离心式压缩机、离心泵等设备上的非接触式机械密封,是在动环或静环密封端面上开设型槽,利用流体动力学原理形成流体动力楔,以达到减小密封端面磨损或泄漏的目的[1-3]。然而,这些机械密封,无论是干气密封还是上游泵送机械密封,它们形成流体动压的介质都是泵入槽内的,在型槽根部产生端面开启力[4-5],但分离动环与静环的同时干气密封会因此增大动、静环间的泄漏率,上游泵送机械密封会出现低压侧流体进入密封腔而污染被密封介质的现象,如果泵送介质含有颗粒还会破坏密封坝端面,加速密封失效[6]。美国专利[7]公开的“一种流体动压型双列螺旋槽端面密封装置”、中国专利[8-9]公开的“双环带螺旋槽端面密封”以及“双列流体型槽自润滑非接触式机械密封”,利用一列螺旋槽将密封流体向下游泵送,另一列螺旋槽将密封流体向上游泵送,并通过这两列螺旋槽所产生的泵汲压差与密封端面内外两侧流体压差相平衡,有效地调和了大开启力与小泄漏率这一矛盾要求。但是,这类密封的结构比较复杂,安装空间大,而且仅适用于密封端面两侧流体压差不大的工况。
为了简化结构、减小安装空间,保证密封性能,根据文献[10]提出了一种适用于密封端面两侧流体压力差范围较为宽泛的自泵送机械密封,并拟通过建模、确定边界条件以及分析计算探讨几何参数和工况参数对自泵送流体动压型机械密封性能即端面开启力和泄漏率的影响,阐释自泵送流体动压型机械密封获得良好密封性能的理论基础,以期为进一步深入研究及其工业应用提供依据。
1 新型自泵送流体动压型机械密封的端面结构及工作原理
1.1 端面结构
图1为自泵送流体动压型机械密封的动环端面结构。动环端面由槽区和密封坝构成,槽区分布在端面的外侧部位,密封坝分布在端面的内侧部位,槽区开设有型线为对数螺旋线的螺旋槽,两螺旋线前端采用圆弧连接,螺旋槽之间的密封面构成密封堰。螺旋槽型线的极坐标表达式[11]为


图1 自泵送流体动压型机械密封的动环端面结构Fig.1 Ring face structure of self-pumping mechanical seals
式中,rg为槽根半径,θ为转角,α为螺旋角。
流体出口位于动环密封面的外径处,进口为位于螺旋槽根部、开设于动环面的与密封腔连通的轴向孔道,孔的圆心即为螺旋槽顶端圆弧的圆心。
1.2 工作原理
参照离心泵工作原理,本研究定义动环旋转时使介质加速成高速流体的螺旋槽侧面为工作面,另一侧面为非工作面,如图2所示。在离心力作用下,高速流体沿工作面切向向动环外径侧流动而泵送至密封腔内;流体在由型槽根部向开口处流动的过程中,由于型槽流通截面扩大,流体流动的速度降低,转化为分离动、静环密封端面的流体压力能;此时,密封腔内的介质无法通过流体型槽高压区屏障并克服密封坝的阻力泄漏至密封面内径侧而被密封。当型槽根部流体流出后,形成了低压区,密封腔内的介质在压差作用下通过动环上与密封腔连通的轴向孔道流进型槽中,同样由型槽工作面加速成高速流体,在离心力作用下沿工作面切向向动环外径侧流动而泵送至密封腔内,如此往复,形成一次次自泵送循环。
类似于离心泵,自泵送流体动压型机械密封的能量头H(包括流体压力能和流体动能)与槽内介质流量Q之间的关系[12]及泄漏率qL与密封面两侧压差Δp之间的关系[13]可分别表示为
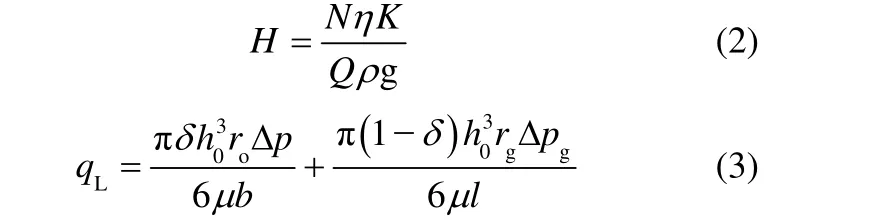
式中,K为与流体槽数相关的环流系数,恒小于1,槽数无限多时趋近于1;η为泵送效率,η=ηmηhηv(ηm为机械效率,ηh为水力效率,槽浅,取小值;ηv为容积效率),反映能量损失的程度;N为轴功率;Q为流体流量;ρ为密封介质密度;qL为泄漏率;δ为槽台宽比;μ为密封介质动力黏度;h0为密封环非槽区流体膜厚度;Δp为密封端面两侧压差;Δpg为密封坝两侧压差;ro为流体膜外半径;b为密封面宽度;l为密封坝宽度。
2 数值分析模型
2.1 基本假设
流体膜润滑机械密封的流场计算十分复杂[14]。为了简化计算,兼顾密封环结构和密封系统本身特性,基于流体力学基本理论,对流体膜进行了如下假设:
① 密封端面间的流体流动为连续介质流动,而且流体温度、黏度保持不变;
② 密封端面间流体属于牛顿流体,做层流流动,剪切应力与速度梯度呈正比;
③ 膜厚很薄,认为在膜厚方向上流体的压力和密度保持常值;
④ 密封环温度、密封材料性质不随时间变化;
⑤ 流体介质与密封表面之间无相对滑移;
⑥ 密封端面光滑,忽略密封端面粗糙度对流体流动的影响。
2.2 采样计算区域几何模型
本文所研究的自泵送流体动压型机械密封,其螺旋槽在密封端面内均布,流体流过的区域为密封端面间周向均布有凸台(对应动环上的螺旋槽)的环形薄片结构间隙。由于流场是轴对称的,理论上各螺旋槽区域的流场相同,考虑到三维建模及网格划分对计算机运行速度的影响,取其中任一螺旋槽区域进行计算[15]。若端面开槽数为Ng,选择整个密封端面的1/Ng区域,即一个槽台区和与之相连的坝区作为计算区域,如图2中区域ABCD 所示。

图2 采样计算区域Fig.2 Sampling calculational region
2.3 控制方程
根据基本假设和几何模型,密封端面间的流体做稳态流动,满足Reynolds 方程[16-17]

对式(4)进行量纲1 化处理得

式中,X=x/ri,Y=y/ri,P=p/pi,Λ=6μriU/(pic2),H=h/c;ri为密封端面内半径,pi为内径侧压力,h为槽深,c为非槽区液体膜厚,U为端面平均线速度,Λ为量纲1 压缩数。
上述方程是一个非线性偏微分方程,不能直接用解析法求解,只能用数值方法求解。本研究采用计算机模拟求解上述偏微分方程,从而获得液膜的压力分布及流速分布。
2.4 边界条件设置
Reynolds 边界条件较为接近真实液膜分布情况,而且在数值处理过程中相对简单[18-19],因而本研究采用Reynolds 边界条件作为两类边界条件。
(1)强制性边界条件Ω1在内径出口AB 面上有p=pi(大气压);在外径出口CD 面上有p=po(介质压力);在轴向孔道进口E处有p=po(介质压力)。
(2)周期性边界条件Ω2在边界AD 和BC 面的压力相等:p|AD=p|BC,即p(θ+2π/Ng)=p(θ)。
根据质量流量守恒,流过边界AD 和BC 面的质量流量相等:q|AD=q|BC;流过AB+DC 面的流体质量等于流过引流孔E 的流体质量:q|E=q|CD+q|AB。
2.5 网格划分及求解器
由于流体膜厚方向的尺寸与径向尺寸差别高达4 个数量级,使用Gambit 软件自动划分网格技术对采样计算区域进行网格划分时难以满足计算过程对网格的精细要求,故采用线-面-体网格划分顺序手动划分网格,以保证在流体膜厚度方向上可划分出多层网格。其中,对边线的划分方式采用Interval count 划分,平面采用Tri 元素下的pave 方式划分,再利用Cooper 方法生成流体膜和型槽部分的网格;对于细长的介质进口孔采用Tet/Hybrid 元素下的TGrid 方式划分网格。网格数太少,会使计算结果产生过大的误差;网格数太多,意味着运算量大、耗时长,而且当网格数增加到一定数量时对结果的精度影响很小。本研究考虑到划分后的网格质量及计算机的运算能力,不断改进网格划分数量,最终将膜厚方向划分为4 层网格,槽深方向划分为5 层 网格,生成的总网格数为440002。划分好的模型如图3所示。
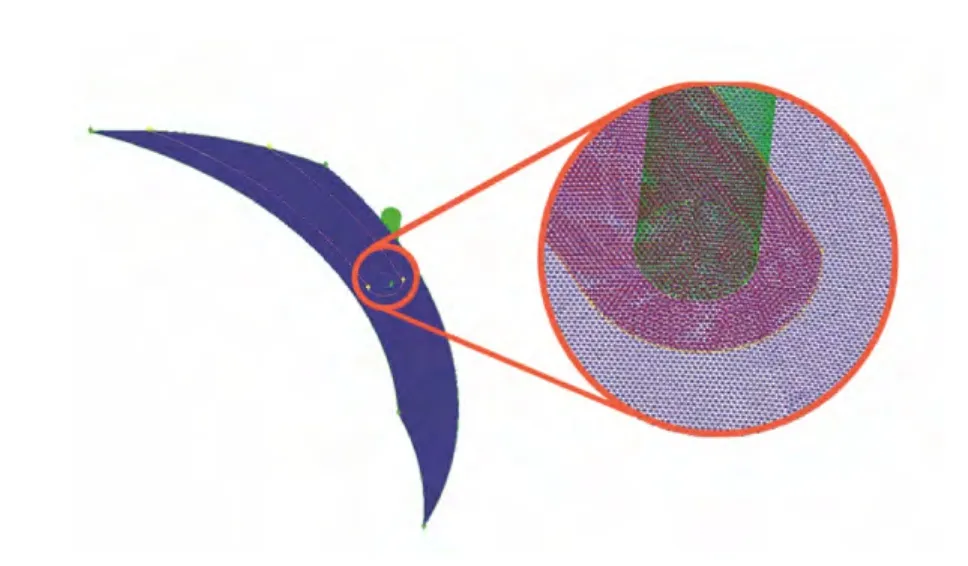
图3 网格划分Fig.3 Mesh generation
选择Fluent3D 三维单精度求解器。求解器模型设置为无黏性(理想)流体,流态选择层流,压力速度耦合采用SIMPLEC 算法,扩散项的离散格式采用中心差分格式,对流项的离散格式采用二阶迎风格式,以提高计算结果的精度。模型收敛绝对精度设为10-8。
3 结果及讨论
影响自泵送流体动压型机械密封性能的因素可分为几何参数和操作参数。几何参数主要有螺旋角α,槽深hg,槽台宽比δ,槽长坝长比γ,槽数Ng,密封端面的内、外半径ri和ro,介质进口孔径d等;操作参数主要有主轴转速n,介质压力po和密封环非槽区流体膜厚度h0等。
为了便于分析和比较,这里选用常温水作为密封介质,取定压力po=4.013×105Pa,黏度μ=1.003×10-3Pa·s,密封端面外半径ro=50 mm、内半径ri=30 mm,密封腔外侧压力pi=1.013×105Pa,主轴转速n=3000r·min-1;同时考虑保证密封端面间有适当的液膜刚度、开启力、较小的泄漏量以及标准中对密封端面的不平度及粗糙度的要求,取h0=1.2 μm。
3.1 流体膜压力及流速分布
图4所示为密封端面的液膜压力云图(图中压强均为表压)。由离心泵的工作原理可知,离心泵叶片入口附近液体的压强等于或低于输送温度下液体的饱和蒸气压时液体将会部分汽化,图4(a)所示为hg=5 μm 时槽内出现的负压区压强远低于工作温度下水的饱和蒸气压,故流场中将会形成空化现象,此时能量损耗较大,表现出的端面开启力较小;图4(b)描述了hg=40 μm 时自泵送机械密封的压力分布,此时负压区消失,具有较大的端面开启力。
进一步研究还发现,当hg<20 μm 时密封端面都会形成负压区,当hg≥20 μm 时负压区消失。

图4 密封端面间液膜压力云图Fig.4 Pressure nephogram of liquid membrane between seal faces

图5 密封端面间液膜速度云图Fig.5 Velocity nephogram of liquid membrane between seal faces hg=40 μm,po=0.3 MPa,n=3000 r·min-1
图5为hg=40 μm 时自泵送流体动压型机械密 封的速度分布云图。由图可以看出,进口孔及螺旋槽之间的流体流速较大,流体主要集中在这部分区域,密封环非槽区流体膜速度极小,内径处的流体流速接近零。实际上,对于hg≥20 μm 的型槽都存在这一规律,这也为构建零泄漏自泵送流体动压型机械密封提供了理论基础。
3.2 结构参数对密封性能的影响
3.2.1 槽深对密封性能的影响 从图6可以看到,总体上自泵送机械密封的开启力随槽深的增大而增大,在5~20 μm 区间出现了急速增大的现象,在20~40 μm 区间出现急速减小的现象。类似于离心泵,在一定的功率下螺旋槽产生的能量头H与螺旋槽输出的流体流量Q呈反比。

图6 槽深变化对密封性能的影响Fig.6 Influence of groove depth on sealing performance Ng=12,δ=0.5,γ=0.5,d=2 mm,α=22°
在hg从5 μm 逐渐增大至20 μm 的过程中,槽内压力从负压增大至0,流体通流截面积随槽深的加大和负压区的消失而急速增大,流速C急剧降低;伴随着阻力系数ζ随槽深增大而减小,流体流动阻力Ω=ζC2/2g迅速减小,泵送效率急剧增大,流体动压能增大,体现在开启力上,其值随槽深的增大快速增大。
在hg从20 μm 逐渐增大至40 μm 的过程中,槽内压力转变为正压,流体流量随槽深增大而增大,而槽深的增大使得边界层的影响减弱,阻力系数ζ下降,提高了泵送效率。由H40/H20=Q20η40/ Q40η20可以看到,在槽深增大至2 倍深时,只要η40/η20<2,则H40/ H20<1,即开启力减小,当槽深增大至40 μm时开启力降至最小值。
随着槽深继续加大,在hg>40 μm 后,流体阻力仍在不断减小,泵送效率值不断提升,由于泵送效率增速比流量增大得快,加上槽深增大对流速的影响,此时便出现H>40中的流体动压能大于H40中,即端面开启力在经历hg=40 μm 的最小值之后缓慢增大。
比较图6中开启力曲线和泄漏率曲线,可以看到自泵送流体动压型机械密封的泄漏率随槽深的变化趋势与开启力随槽深的变化趋势相近。这是因为机械密封的泄漏率与密封坝两侧的压差成正比的原因:开启力大,密封坝两侧的压差大,泄漏率随之增大。
3.2.2 槽数对密封性能的影响 如图7所示,密封端面开启力随螺旋槽数量的增多而降低,泄漏率几乎不变。槽数增多,槽内流体流动有序,环流减少,K值增大,但单个螺旋槽截面积变小,边界层影响增强,η降低,致使压力能呈缓慢下降趋势,体现在开启力上,其值随槽数的增多而降低;开启力小,单个计算区域密封坝两侧的压差小,泄漏率随之减小,但又因槽数增多,导致整体泄漏率几乎不变。
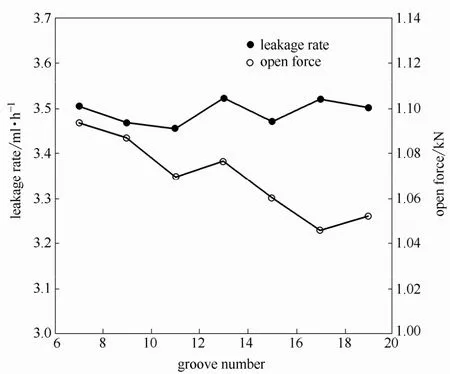
图7 槽数变化对密封性能的影响Fig.7 Influence of groove number on sealing performance hg=40 μm,δ=0.5,γ=0.5,d=2 mm,α=22°
3.2.3 引流孔孔径对密封性能的影响 如图8所示,开启力、泄漏率均随孔径的增大而增加。引流孔径增大,使得流体流入阻力小,提高了泵送效率,而螺旋槽尺寸和转速未变,流量稳定,开启力得到提升;开启力的提升增大了密封坝两侧的压差,加大了泄漏率。

图8 引流孔孔径变化对密封性能的影响Fig.8 Influence of aperture diameter on sealing performance

图9 螺旋角变化对密封性能的影响Fig.9 Influence of helix angle on sealing performance
3.2.4 螺旋角对密封性能的影响 如图9所示,泄漏率及开启力均随螺旋角的增大而增大。螺旋槽工 作面长度随螺旋角的增大而减小,流体流过螺旋槽工作面的沿程阻力随之减小,流体获得的动压能增大,开启力变大;而且,开启力增大,意味着密封坝两端的压力差增大,导致泄漏率不断增大。
3.2.5 槽长坝长比对密封性能的影响 如图10所示,随着槽长坝长比的增大,开启力呈下降趋势,而泄漏率则随槽长坝长比的增大持续增大。槽长坝长比增大,意味着螺旋槽加长,流体流过螺旋槽工作面的沿程阻力增大,流体获得的动压能减少,开启力降低;槽长坝长比增大,使得引流孔位置趋近密封环内径处,即减小了形成流体泄漏阻力的密封坝宽度,尽管开启力降低,但其下降速度远不及密封坝宽度的减小变化,因而导致泄漏率增加。

图10 槽长坝长比对密封性能的影响Fig.10 Influence of ratio of groove length to dam length on sealing performance
3.2.6 槽台宽比对密封性能的影响 如图11所示,随着槽台宽比的增大,螺旋槽宽度增大,流体流过螺旋槽工作面的阻力减小,泵送效率增强,流体获得的动压能多,开启力增大,而开启力的增大意味着密封坝两侧的压力差增大,导致泄漏率不断增大。

图11 槽台宽比对密封性能的影响Fig.11 Influence of ratio of groove width to ridge width on sealing performance
3.3 工况参数对密封性能的影响
在研究工况参数对密封性能的影响时,取定槽数Ng=12,槽深hg=40 μm,槽台宽比δ=0.5,槽长坝长比γ=0.5。
3.3.1 主轴转速变化对密封性能的影响 如图12所示,当转速增大时,螺旋槽泵送效应明显,单位时间内泵送流体获得的动能急剧增多,相应的动压能减少,表现为开启力随转速增大而减小,而且在9000 r·min-1时出现了开启力消失现象。开启力减小,意味着密封坝两侧的压差减小,形成较小的泄漏率;在开启力消失之后,泄漏率出现负值,即产生虹吸现象,将密封腔外侧的介质吸入。

图12 转速变化对密封性能的影响Fig.12 Influence of speed on sealing performance po=4.013×105 Pa
3.3.2 内、外侧压差对密封性能的影响 如图13所示,随着密封端面内、外侧压差的增大,通过引流孔进入螺旋槽进口的流体压力增大,开启力呈线性增大。开启力线性增大,导致密封坝两侧的压差增大,致使泄漏量也呈线性迅速增大。

图13 压差对密封性能的影响Fig.13 Influence of pressure on sealing performance n=3000r·min-1
4 结 论
(1)提出了一种与以往流体泵入型不同的流体泵出型机械密封结构。这种结构的自泵送流体动压型机械密封无须提供隔离流体的辅助系统。通过建立自泵送流体动压型机械密封模型,利用Fluent 计算出流体膜的压力分布云图和速度分布图,以及探讨几何参数和工况参数对密封性能的影响,阐释了其产生流体动压以及形成泄漏率的机理。
(2)揭示了结构参数和工况参数对自泵送流体动压型机械密封性能的影响规律。研究表明,转速增大,开启力和泄漏率均减小;随着介质压力、槽台宽比、引流孔孔径以及螺旋角的增大,开启力和泄漏率均增大;随着槽数、槽长坝长比的增大,开启力均有所降低,泄漏率略有增大;槽深增大对开启力和泄漏率的影响趋势相似,存在一个使得开启力较大而泄漏率较小的槽深;在本研究的计算参数下,当槽深为40 μm 时具有较大的开启力和最小的泄漏率。
(3)在给定的密封工况下,通过调整型槽结构参数,可实现密封端面内径处被密封介质的零泄漏和腔外介质的无侵入。
符 号 说 明
d——介质进口孔径,mm
F——开启力,kN
hg——槽深,μm
h0——密封环非槽区流体膜厚度,μm
Ng——槽数
n——转速,r·min-1
pi,po——分别为进口压力、出口压力,Pa
rg——对数螺旋线起始半径,mm
ri,ro——分别为密封环内径、密封环外径,mm
α——圆周切线与对数螺旋线切线的夹角,(°)
γ——槽的长度与整个密封面宽度之比
δ——圆周上槽的宽度与整个槽台宽度之比
θ——对数螺旋线相对于圆心旋转的角度,rad
[1]Etsion I.A new concept of zero-leakage non-contacting face seal [J].Journal of Tribology,1984,106(3):338-343
[2]Fischbach M J.Dry seal applications in centrifugal compressors [J].Hydrocarbon Processing,1989,68(10):47-51
[3]Lai T.Development of non-contacting,non-leaking spiral groove liquid face seals [J].Lubrication Engineering,1994,50(8):625-631
[4]Wang B,Zhang H,Cao H.Flow dynamics of a spiral-groove dry-gas seal [J].Chinese Journal of Mechanical Engineering,2013,26(1):78-84
[5]Buck G S,Volden D.Upstream pumping:a new concept in mechanical sealing technology [J].Lubrication Engineering,1990,46(4):213-217
[6]Qiu Y,Khonsari M M.Thermo hydrodynamic analysis of spiral groove mechanical face seal for liquid applications [J].Journal of Tribology,2012,134(2):021703-021713
[7]Lai Weitang.Face seal with double spiral grooves[P]:US,5201531A.1993-04-13
[8]Wang Yuming(王玉明),Li Keyong(李克永).End face seal of double loop with S-piral groove [P]:CN,96108614.9.1996-06-22
[9]Hao Muming(郝木明),Hu Danmei(胡丹梅),Ge Jingpeng(葛京鹏),Yang Huixia(杨惠霞).Self-lubricating non-contact mechanical seal with double rows of fluid dynamic pressure groove [P]:CN,00239202.X.2000-06-13
[10]Sun Jianjun(孙见君),Wang Min(王敏),Zhou Min(周敏),Tu Qiao’an(涂巧安).Self-pumping mech-anical seal based on fluid dynamic pressure principle [P]:CN,103267132A.2013-08-28
[11]Hu J B,Tao W J,Zhao Y M,et al.Numerical analysis of general groove geometry for dry gas seals [J].Applied Mechanics and Materials,2014,457:544-551
[12]Li Yun(李云),Jiang Peizheng(姜培正).Peocess Fluid Machiney(过程流体机械)[M].Beijing:Chemical Industry Press,2010
[13]Xia Qing(夏清),Chen Changgui(陈常贵).Principles of Chemical Engineering(化工原理)[M].Tianjin:Tianjin University Press,2009
[14]Li Y,Song P Y,Xu H J.Performance analyses of the spiral groove dry gas seal with inner annular groove [J].Applied Mechanics and Materials,2013,420:51-55
[15]Wang Q,Chen H L,Liu T,et al.Research on performance of upstream pumping mechanical seal with different deep spiral groove//IOP Conference Series:Earth and Environmental Science [C].IOP Publishing,2012,15(7):072019-072027
[16]Basu P.Analysis of a radial groove gas face seal [J].Tribology Transactions,1992,35(1):11-20
[17]Nicolescu B N,Petrescu T C.Homogenization of the Reynolds equation in the radial face seals case [J].Asymptotic Analysis,2013,81(1):35-52
[18]Ruan B.Finite element analysis of the spiral groove gas face seal at the slow speed and the low pressure conditions-slip flow consideration [J].Tribology Transactions,2000,43 (3):411-418
[19]Hu X P,Song P Y.Theoretic analysis of the effect of real gas on the performance of the T-groove and radial groove dry gas seal [J].Applied Mechanics and Materials,2013,271:1218-1223
