参数灵敏度反馈车辆半主动悬架控制
2015-08-19张立军
张立军
(辽宁工业大学 汽车与交通工程学院,辽宁 锦州121001)
参数灵敏度反馈车辆半主动悬架控制
张立军
(辽宁工业大学汽车与交通工程学院,辽宁锦州121001)
为解决悬架控制器对车辆参数和行驶工况参数变化的适应性问题,不同于以往的自适应、自校正控制方法,将参数灵敏度引入控制系统中,以降低参数灵敏度为目标进行车辆半主动悬架系统控制研究。控制系统的反馈由状态反馈和灵敏度反馈两部分组成。应用该方法在常用车辆参数和行驶工况参数下设计控制器,并与传统的LQR控制器进行比较。研究表明,在车辆参数和行驶工况参数不变情况下,灵敏度反馈方法所得车身加速度和轮胎变形增益比二次型最优方法减小6 dB~8 dB;两种方法所得悬架动挠度基本接近。此外,当路面激励增加、车速提高和车辆载荷减小时,灵敏度反馈方法比二次型最优方法具有较好的鲁棒性。
振动与波;车辆;半主动悬架;参数灵敏度;反馈;二次型最优
车辆悬架系统性能的优劣不仅取决于悬架系统参数,也受到行驶工况参数的影响,如行驶路面、行驶车速参数的影响。因此无论是传统被动悬架系统的参数优化,还是主动、半主动悬架控制,都试图解决车辆参数和行驶工况参数变化时的悬架性能适应性问题。上世纪80年代末国外首先提出了自适应悬架的设计思想,即控制器参数是可变的,以适应当前的路面、车速和载荷[1,2]。国内在这方面的研究也取得了许多进展,文献[3]提出基于增益规划和Kalman状态估计相结合的自校正控制算法,使控制器参数适应于路面输入及车辆参数的变化;文献[4]应用神经网络辨识模型参数,进行悬架自适应控制;文献[5]以天棚阻尼半主动悬架为参考模型进行自适应控制器设计;文献[6,7]应用最小方差自适应算法调整控制器参数;文献[8,9]对半主动悬架的参数进行了优化匹配研究。以上研究多以参数辨识为前提,通过实时调整控制器参数来解决悬架控制的性能适应性问题。本文从另一角度探讨这一问题,将系统参数灵敏度引入控制系统中,以降低参数灵敏度为目标进行车辆半主动悬架系统控制研究,探讨用参数灵敏度反馈解决车辆悬架控制的性能适应性问题,用此方法进行车辆悬架控制未见有文献报导。
1 悬架系统控制模型
由于本研究以探讨新的悬架控制方法为目的,因此选取有代表性的1/4车辆悬架控制模型,如图1所示。

图1 1/4车辆半主动悬架模型
设如下状态变量

于是可得如下状态方程

式中zb、zw分别为车身垂直位移和车轮垂直位移;mb、mw分别为车身质量和车轮质量;ks为悬架刚度;cs为悬架阻尼;kt为轮胎刚度;U(t)为悬架阻尼控制力;z0为路面输入。
式(2)—(5)可写成状态方程形式

式中

2 含灵敏度反馈的增广控制系统模型
2.1系统灵敏度控制模型
设系统可变参数向量为α,研究主要考虑车辆载荷、路面输入和车速参数变化,其他参数如悬架刚度、阻尼等参数变化幅度较小不予考虑。于是系统状态变量的灵敏度向量为

将式(7)对α求偏导,得系统灵敏度控制模型

由于系统控制变量可表达如下

根据LQR可得最优反馈增益矩阵

P为如下Riccati方程的解
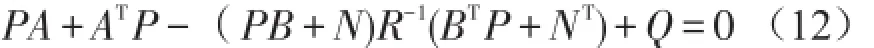
式中Q、R、N为性能指标加权矩阵。
将式(11)对α求偏导,其中不考虑加权系数矩阵NT的灵敏度,于是可得
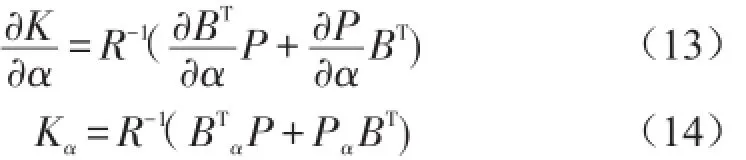

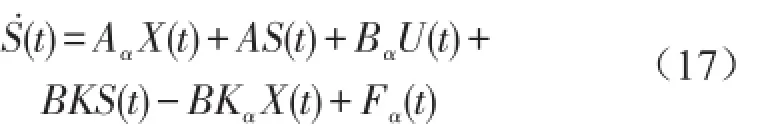
式(17)即为系统灵敏度控制方程。
2.2含灵敏度模型的增广控制系统模型
设增广状态向量为

于是由式(1)和式(7)得增广控制系统模型
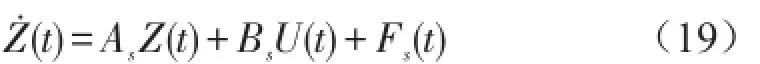
式中
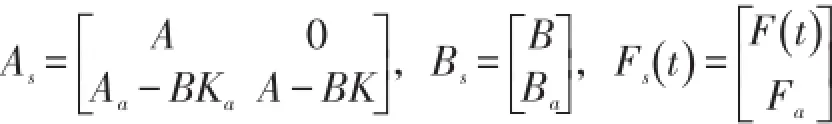
其中

增广系统最优控制力为
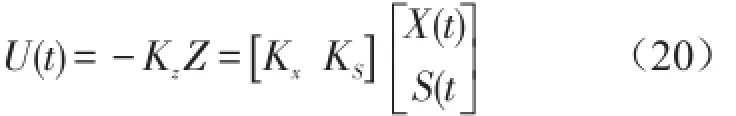
根据式(18)和式(20),可得含灵敏度反馈的悬架控制系统框图,如图2所示。

图2 含灵敏度反馈的悬架控制系统框图
增广系统的Riccti方程为

增广系统最优反馈增益矩阵为
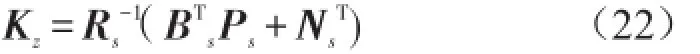
3 控制仿真及分析
3.1参数不变时的控制结果比较
仿真以满载载荷、车速u=20 m/s为典型工况进行灵敏度反馈控制器设计。为了与传统的二次型最优LQR方法对比分析,在相同工况下也设计了二次型最优LQR控制器。仿真车辆模型参数如表1所示。
根据式(22)得增广系统最优反馈增益矩阵Kz:

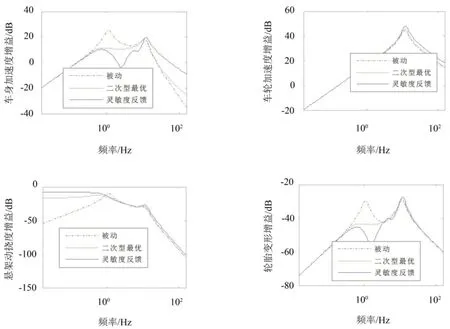
图3 悬架各响应增益比较

表1 仿真车辆模型参数
将上述结果代入式(20),即可求出含灵敏度反馈的系统响应。图3为车身加速度、车轮加速度、悬架动挠度和轮胎变形的增益曲线。从该图可以看出,车身加速度在车身固有频率1.15 Hz(7.27 rad/s)附近,灵敏度反馈和二次型最优方法所得峰值接近,均比被动悬架峰值减小约20 dB;在4 Hz左右灵敏度反馈方法比二次型最优方法峰值减小约8 dB。车身加速度在车轮固有频率附近,三种方法所得峰值相等,这符合悬架控制的不动点理论,即车身加速度在车轮固有频率附近有一不动点,无论采用何种控制方法也不能改变其峰值大小。此外,三种方法所得车轮加速度增益峰值基本相等,这也是悬架不动点理论的间接表现。在车身固有频率附近,灵敏度反馈方法所得悬架动挠度峰值比二次型最优方法和被动悬架略高,在其他频率段三种方法所得悬架动挠度基本相同。轮胎变形在车身固有频率附近,灵敏度反馈方法与二次型最优方法所得峰值相当,均比被动悬架减小约22 dB;在4 Hz左右,灵敏度反馈方法比二次型最优方法峰值减小约6 dB。
3.2参数变化时的控制器鲁棒性分析
分析当车辆车速、路面和载荷变化而控制器参数不变时的控制效果。为反映路面和车速的变化,在此采用时域分析。路面输入采用凸块输入(也可采用随机输入),其表达式如下
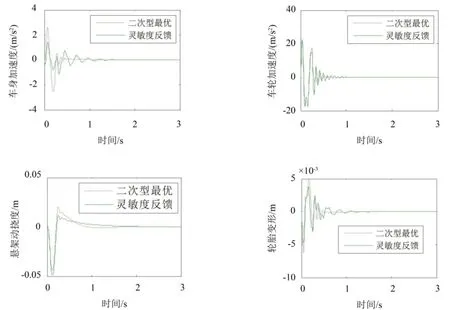
图4 悬架参数变化时各响应时间历程比较
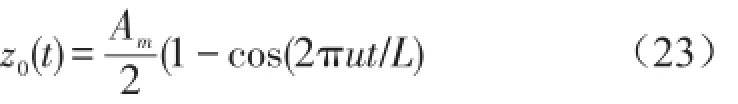
其中Am为路面凸块高度,L为凸块长度。
图4为路面图块高度由Am=0.05 m增加到Am=0.1 m;车速由u=20 m/s增加到u=40 m/s;车辆载荷由满载减小到半载时的时域响应比较。从图4可以看出:除车轮加速度外,当车辆参数变化时,参数灵敏度方法比二次型最优方法控制效果好,而且鲁棒性强。
4 结语
(1)将参数灵敏度反馈引入到车辆半主动悬架控制中,建立含灵敏度反馈的增广悬架系统控制模型,实现了状态反馈和灵敏度反馈联合控制;
(2)分析表明参数灵敏度反馈控制器性能优于二次型最优控制器,而且当车辆参数变化时具有较好的鲁棒性,特别是对于车身加速度指标效果更明显。
[1]HacA.Activecontrolofvehiclesuspension[J]. International Journal of Vehicle System Dynamics,1987,(16):57-74.
[2]Hen H F,Guenther D A.Self-tuning optimal control of an active suspension[J].SAE Paper,892485.
[3]喻凡,郭孔辉.车辆悬架的最优自适应与自校正控制[J].汽车工程,1998,20(4):193-200.
[4]陈无畏,王志君,范迪彬.汽车半主动悬架的神经网络自适应控制[J].汽车工程,1998,20(1):31-36.
[5]郑玲,邓兆祥,李以农.汽车半主动悬架的模型参考自适应控制[J].中国公路学报,2005,18(2):99-102.
[6]曹民.主动悬架的参数估计自校正控制[J].汽车工程,2001,23(3):177-180.
[7]孙建民,王芝秋,张新玉.车辆主动悬架系统的LMS自适应控制[J].汽车工程,2003,25(4):360-363.
[8]姚晶晶,徐中明.对地友好性的悬架参数优化及半主动控制[J].噪声与振动控制,2014,34(5):57-60.
[9]陈昆山,靳慧鲁.混合型主动悬架电磁反力作动器的匹配研究[J].噪声与振动控制,2010,30(5):1-5.
Control of Semi-active Suspension of Vehicles Based on Parameter Sensitivity Feedback
ZHANG Li-jun
(College ofAutomobile and Traffic Engineering,Liaoning University of Technology,Jinzhou 121001,Liaoning China)
In order to improve the adaptation of suspension controllers to vehicle and operation parameters,the parameter sensitivity analysis was introduced to the suspension control system to reduce the parameter sensitivity.This method was different from the conventional adaptive and self-tuning methods.The control system was composed of state feedback and sensitivity feedback.Applying this method,the controller was designed with the conventional vehicle and operation parameters used.The results were compared with those of the LQR controller.The research shows that the gains of body acceleration and tire deflection obtained by parameter sensitivity feedback can be decreased by 6-8dB in comparison with the LQR controller.The suspension deflections by the two methods are close to each other.In addition,parameter sensitivity feedback has better robustness than the LQR in strong excitation,high velocity and small load cases.
vibration and wave;vehicle;semi-active suspension;parameter sensitivity;feedback;LQR
U461.1
ADOI编码:10.3969/j.issn.1006-1335.2015.05.014
1006-1355(2015)05-0069-04
2014-10-31
张立军(1963-),男,辽宁省昌图县人,博士,教授。主要研究方向:车辆系统动力学及控制。
Email:lgzlj2008@sohu.com
