基于联合稀疏恢复的宽带雷达动目标检测方法
2015-08-17明戴奉周刘宏伟王小谟秦西安电子科技大学雷达信号处理国家重点实验室西安710071中国电子科学研究院北京100041
方 明戴奉周*刘宏伟王小谟秦 童(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)(中国电子科学研究院 北京 100041)
基于联合稀疏恢复的宽带雷达动目标检测方法
方 明①戴奉周*①刘宏伟①王小谟①②秦 童①
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(中国电子科学研究院 北京 100041)
针对宽带雷达目标回波存在越距离单元走动的问题,该文提出一种基于联合稀疏恢复的宽带雷达动目标检测方法。该方法先在频域对回波数据进行预白化处理,抑制杂波;然后在频率-慢时间域推导出目标信号的联合行稀疏表示,并通过联合稀疏恢复算法得到目标的频域估计;最后通过逆傅里叶变换得到目标的时域估计。仿真结果验证了该方法的有效性。
宽带雷达;目标检测;越距离单元走动;杂波抑制;联合稀疏恢复
1 引言
随着现代雷达技术的发展,宽带雷达因其能够获得更多的目标信息、更高的参数辨别能力,从而得到了广泛的应用[1-8]。此外,宽带雷达提高了雷达的距离分辨率,降低了每个距离单元的杂波功率,在一定程度上提高了信杂比,进而改善雷达在杂波背景下的检测性能[9]。但是宽带雷达由于距离分辨单元较小,运动目标即使在不长的相干处理时间间隔(Coherent Processing Interval, CPI)内也极易发生越距离单元走动,导致脉冲间目标回波包络位置的错开,这样就造成了难以用传统的方法实现杂波抑制以及目标的相干积累。
因此对于宽带雷达,为了实现有效的杂波抑制和目标的相干积累,必须克服越距离单元走动问题。在雷达成像领域中,文献[10-12]为了解决运动目标的越距离单元走动问题,提出利用Keystone变换实现目标回波多普勒“聚焦”进而完成回波包络的对齐。Keystone变换适用于多目标场景,但是要求场景内的所有目标不模糊或者具有相同的模糊次数,若是出现多个模糊次数不等的目标时,该方法无法同时校正所有目标的越距离单元走动[12]。
针对上述问题,本文提出一种基于联合稀疏恢复的宽带雷达动目标检测方法。该方法先在频域利用杂波协方差矩阵(Clutter Covariance Matrix,CCM)的Cholesky分解对回波数据进行预白化;然后在频率-慢时间域推导出目标信号的联合行稀疏表示,并通过联合稀疏恢复算法得到目标场景的频域估计;最后通过逆傅里叶变换得到目标场景的时域估计。本文通过仿真实验表明:在多目标场景下,该方法可在杂波背景中有效地重构出目标场景。本文结构如下:第2节首先介绍宽带雷达的信号模型及目标信号的非模糊表示;第3节给出基于联合稀疏恢复的目标检测算法,包括回波数据预白化以及目标信号的联合行稀疏表示与恢复;第4节利用仿真实验验证算法性能;最后在第5节总结全文。
2 信号模型与目标信号的非模糊表示
2.1 目标模型
设雷达发射信号为线性调频信号,一个相干处理时间间隔内的脉冲数为M,脉冲重复间隔(Pulse Repetition Interval, PRI)为 Tr。在窄带雷达中,目标检测通常是沿着距离单元挨个进行,而对于宽带雷达,由于目标回波存在越距离单元走动问题,因此选取一段长度为K的相邻距离单元做为检测单元,并且在其附近选取一段长度为aK的距离单元为参考单元,如图1所示。则匹配滤波后,目标回波信号在频率-慢时间域可表示为[13]
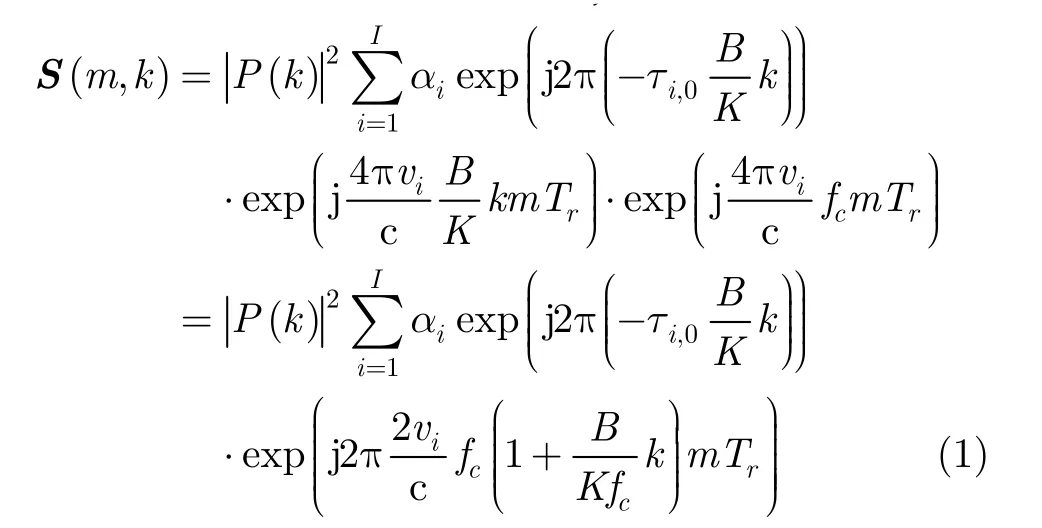
其中k表示频率,m表示慢时间,I表示目标场景内散射点个数, αi,τi,0,vi分别表示第i个散射点的复振幅,初始时延以及速度,c表示光速, fc表示雷达载频,B表示发射信号带宽,P(k)表示发射信号的频谱。式(1)第1个等式中的第2个指数项表示包络平移;将式(1)第1个等式中的后两个指数项合并,得到第2个等式的第2个指数项,其中 2vifc(1表示目标的多普勒频率,它与频率k线性耦合,即所谓的多普勒色散。
2.2 目标的非模糊表示
针对本文所研究的问题,当雷达脉冲重复频率(Pulse Repetition Frequency, PRF)较低,或目标运动速度较大时,目标存在多普勒模糊现象,应对其进行相应的处理。
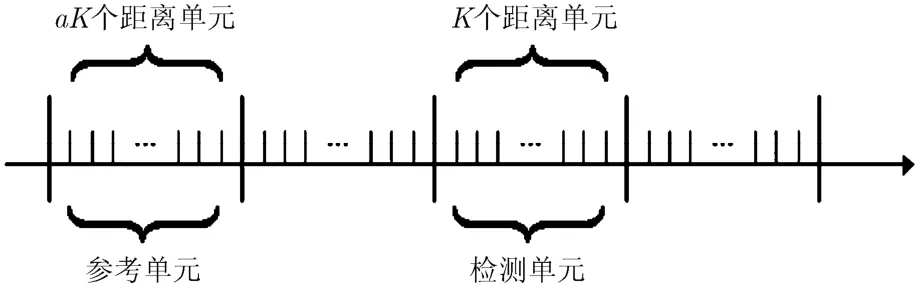
图1 宽带雷达目标检测示意图

为了消除多普勒模糊,本文采用采样内插恢复的原理得到目标信号的非模糊表示[14]:
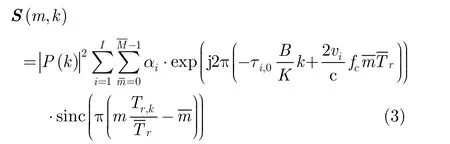
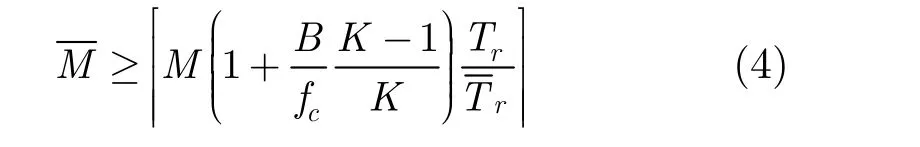
2.3 杂波模型
早期基于低分辨率雷达的以中心极限定理为基础的高斯模型,由于比较简单且可以较好地描述窄带雷达杂波,因此获得广泛应用[15]。但是对于宽带雷达,较高的距离分辨率会使每个距离单元内独立散射体较少,导致中心极限定理不再适用,进而造成高斯模型的失效。
球不变随机向量(Spherically Invariant Random Vector, SIRV)常用来描述宽带雷达杂波[16]。根据球不变随机向量模型,不同距离单元内的杂波可以表示为
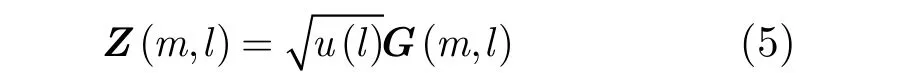
其中l = 1,2,…, L表示距离单元序号,u(l)为基本幅度调制分量,用来描述杂波第l个距离单元的杂波功率,G中所有的列向量都是与u(l)统计独立的M维零均值复高斯随机向量,并且具有相同的归一化协方差矩阵在该模型中,均匀杂波指所有距离单元的杂波功率相等,部分均匀指检测单元与参考单元中的杂波都是均匀的,但是它们之间的功率不相等。
将检测单元与参考单元的杂波数据分别变换到频率-慢时间域,根据文献[17]对宽带雷达杂波性质的讨论,若杂波在慢时间-距离域是均匀的或部分均匀的,则在频率-慢时间域,参考单元与检测单元的杂波归一化协方差矩阵是相同的,但它们的功率可能是不等的。
3 回波数据预白化与目标信号的联合稀疏表示、恢复
3.1 回波数据预白化处理
根据上一节中给出的频率-慢时间域的目标和杂波模型,那么雷达的接收信号可表示为
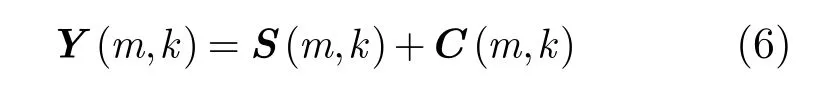
其中 C (m,k)表示第m次回波第k个频率单元的杂波。为方便以下推导,将频域回波表示为列向量的形式:

由于雷达回波中往往存在很强的杂波分量,如果不对其采取有效方法进行抑制,则很难保证理想的检测性能。针对此问题,本小节采用白化的方式对回波数据进行预处理。
不失一般性,假设杂波是部分均匀的,则检测单元的杂波协方差矩阵可按照式(8)方式构造:
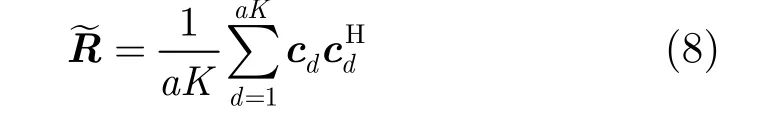
其中 cd表示参考单元中的样本数据(频率-慢时间域)。利用杂波协方差矩阵R~对检测单元中的回波数据做预白化处理,得到白化后的回波数据:

3.2目标信号的联合行稀疏表示
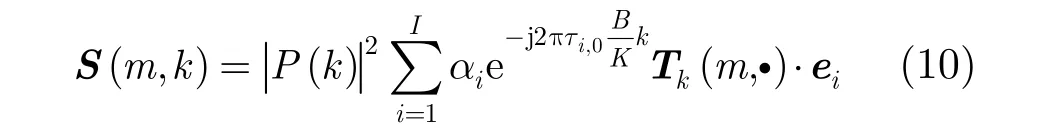
其中 Tk(m,·)表示矩阵 Tk的第m行。
由式(10),目标向量可进一步表示为
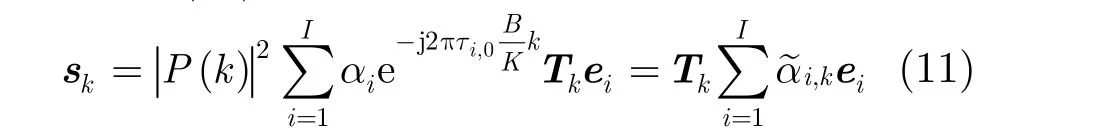
由式(11)的目标回波模型可知,如果我们能够获得各个散射点在每个频率单元的复幅度估计,之后再对其进行逆傅里叶变换,这样便可得到目标场景的时域估计。为此,先将多普勒频率量化为Q个分辨单元,这样式(11)就可以用矩阵形式表示为

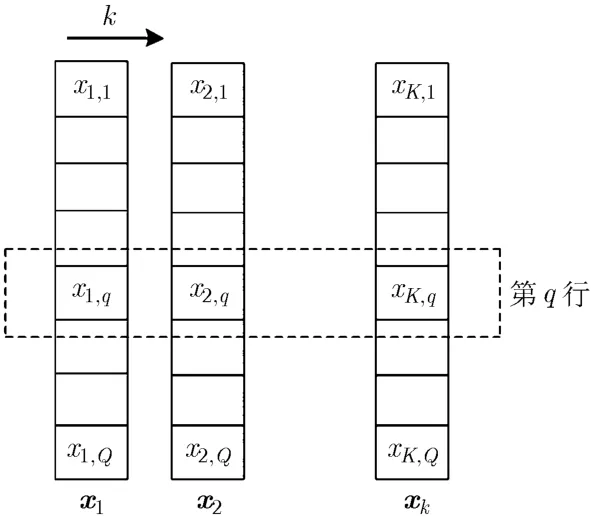
图2 系数矩阵的行稀疏特性
结合式(9)和式(12),则预白化后的回波数据可表示为
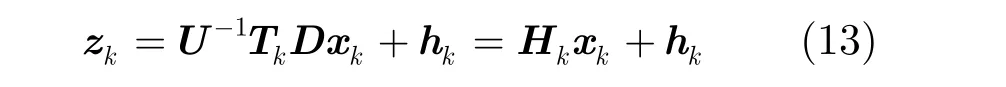
3.3 目标信号的联合稀疏恢复
如3.2小节所述,在频率-慢时间域,目标信号可由一组傅里叶基线性表示,且目标信号在该基底下的系数 xk是稀疏的。根据压缩感知(Compressed Sensing, CS)理论,当信号能稀疏表示时,利用该稀疏先验,可实现少量样本情况下的信号恢复[18]。此外,系数矩阵X还具有一定的结构特性(行稀疏),稀疏恢复时若能合理利用这种结构特性,则可进一步提高目标信号的恢复效果[19]。由文献[20]可知,当信号的系数矩阵具有行稀疏特性时,那么从被复高斯白噪声污染的观测值中恢复目标的问题可以描述为
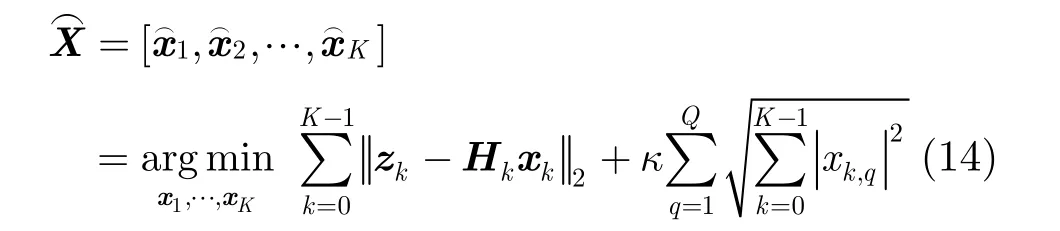

其中F为逆傅里叶变换矩阵。
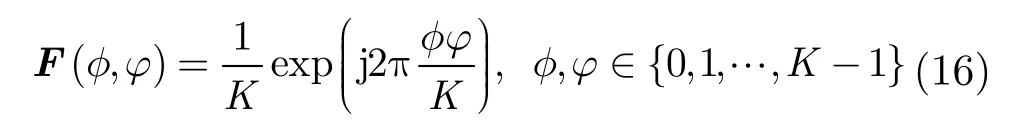
4 仿真实验
4.1 实验设置
4.1.1 系统参数设置雷达的系统参数如表1所示。

表1 系统参数
4.1.2 杂波场景设置
杂波的随机起伏特性可用概率密度分布函数和功率谱表示。在高分辨雷达中,一般用韦布尔分布(Weibull)和K分布等非高斯模型来表示杂波幅度的概率密度函数[15],因此本文假设回波中杂波的幅度服从韦布尔分布。通过对宽带雷达地杂波实测数据的分析,具有如式(17)形式的幂率功率谱模型可以较好地拟合实测杂波的功率谱密度[17]。
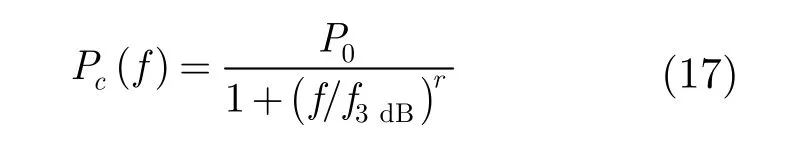
对于本文设定的实验参数,r = 3;P0是杂波功率,f3dB是杂波的半功率带宽。
4.1.3 目标场景设置本文参考文献[14],将目标场景内每个散射点的信杂比(Signal-to-Clutter Ratio,SCR)定义为
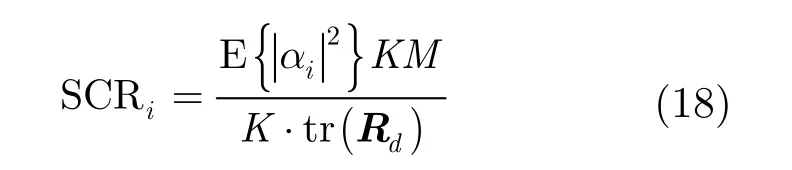
其中 Rd表示检测单元的真实杂波协方差矩阵(频率-慢时间域),tr(·)表示求矩阵的迹。
假设目标场景内共 3个目标,每个目标包含6个散射点,其中目标3为强目标,目标1及目标2为弱目标,且每个散射点的距离、归一化多普勒频率及信杂比如图3所示。
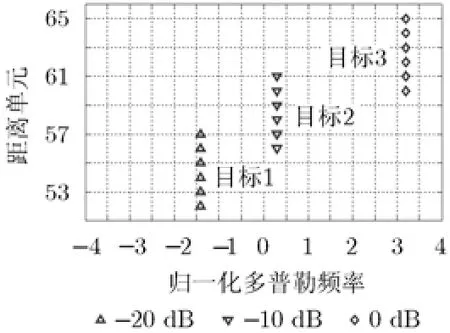
图3 目标场景示意图
图4(a)~4(c)分别给出了目标1,目标2及目标3的越距离单元走动情况,从图中可以明显地看出目标1和目标3发生了越距离单元走动,其中目标1的走动量约为4.5个距离单元,目标3的走动量约为10.2个距离单元。图4(d)表示雷达回波信号的距离-慢时间域,从图中可以看出,两个弱目标完全淹没在杂波中,如果不采取一些处理,则很难将它们检测出来。
图5(a), 5(b)分别表示的是雷达回波信号做Keystone变换前的频率-多普勒域和做Keystone变换后的频率-多普勒域。由图5(a)可以看出,目标的多普勒频率与频率存在耦合,并且目标 1与目标3发生了多普勒模糊(目标1,目标2及目标3的模糊次数分别为-1, 0和3,即目标场景内的目标具有不同的多普勒模糊次数)。在频域对雷达回波数据进行Keystone变换(变换时对目标3解多普勒模糊),得到的实验结果如图5(b)所示。在图5(b)中,目标3的多普勒频率与频率解耦合,并且其能量集中在相应的多普勒单元。而目标1和目标2由于它们的模糊次数与目标3不等,故Keystone变换后,它们的多普勒频率与频率依旧是耦合的,即Keystone变换对具有多个模糊次数的目标场景是失效的。
对于本文算法,为了保证重采样的目标信号不出现多普勒模糊,虚拟采样率可取为7 kHz,相应地,虚拟脉冲数M可取为280,则重采样后目标1,目标 2及目标 3的归一化多普勒频率分别为-0.2000, 0.0429和0.4571,此时3个目标在多普勒域都不模糊,如图6所示。采用本文方法对雷达回波数据进行处理,得到的实验结果如图7所示。从图7可以明显地看出,在杂波背景中,本文方法可以较好地恢复出目标场景,尤其是当场景中存在弱目标时,该方法依然能够将其重构出来。
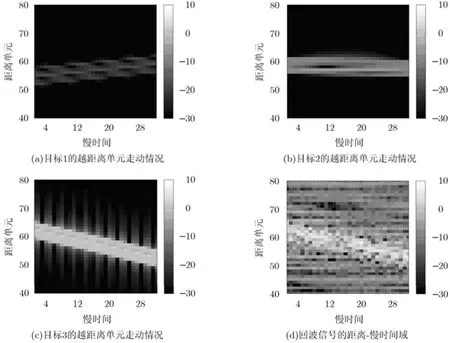
图4 目标回波的越距离单元走动情况以及回波信号的距离-慢时间域

图5 回波数据Keystone变换前后的频率-多普勒域
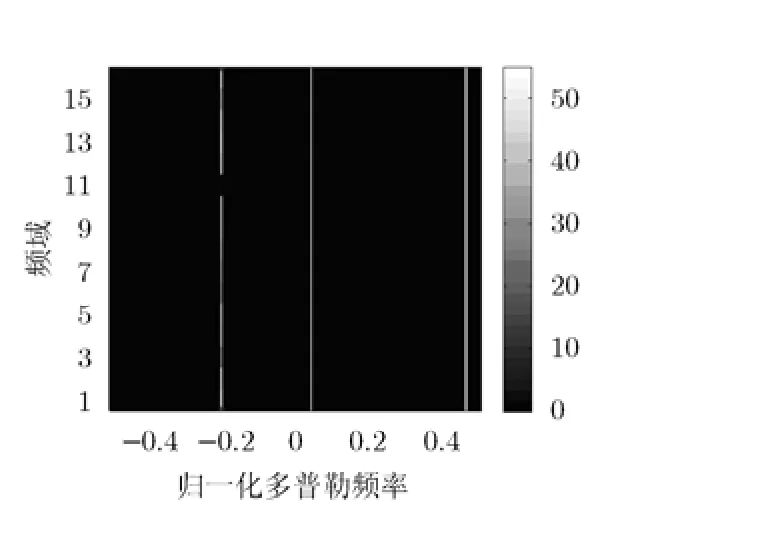
图6 目标信号经重采样后的频率-多普勒域
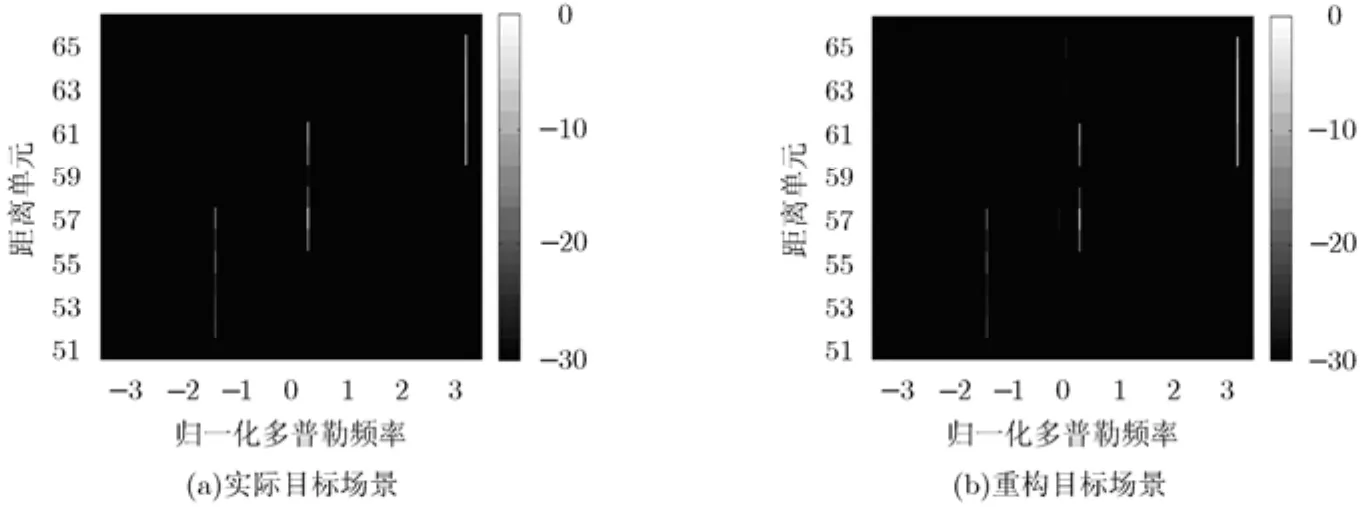
图7 实际目标场景及本文方法重构的目标场景
为了定量地衡量目标场景的重构质量,本文采用Monte Carlo重复试验统计目标的重构误差。在仿真中,定义目标的归一化均方误差(Normalized Mean Square Error, NMSE)为其中 εp表示第p个目标的 NMSE,?表示第p个目标第t次试验时各个散射点的振幅, 是的估计,T是Monte Carlo试验次数,仿真中取为100次,得到的实验结果如表2所示。
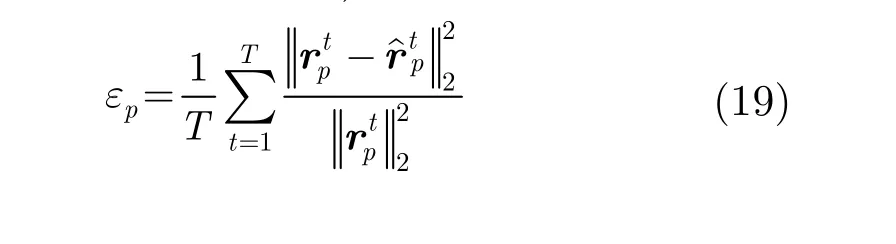
从表2中可以看出本文算法在低信杂比条件下也具有较好的重构性能,进一步验证了本文算法的有效性。

表2 各个目标的归一化均方误差
为了分析本文算法的效率,分别对脉冲数M= 8,16,32的情况进行仿真分析。仿真采用的计算机硬件配置为:Intel Core i7 CPU 4770@3.40 GHz, 3.40 GHz,内存7.89 GB。表3给出了3种情况下算法运行的平均时耗。由表3可以明显看出,随着脉冲数增加,本文算法的计算量急剧增大。因此,如何在保证重构性能的前提下显著降低计算量是本文算法的有待改进之处。

表3 不同情况下算法的平均时耗
5 结束语
本文研究了杂波背景下的宽带雷达动目标检测问题,提出一种基于联合稀疏恢复的宽带雷达动目标检测方法。该方法先在频域利用杂波协方差矩阵的Cholesky分解对回波数据进行预白化;然后在频率-慢时间域推导出目标信号的联合行稀疏表示,并通过联合稀疏恢复算法得到目标场景的频域估计;最后通过逆傅里叶变换得到目标场景的时域估计。本文通过仿真实验表明:在多目标场景下,该方法可在杂波背景中有效地重构出目标场景。然而,本文中的目标场景重构是基于l1范数优化的结果,当脉冲数较多时优化计算量巨大。如何在保证重构性能的前提下降低计算量是未来的研究重点。此外,本文在构造基矩阵时并未考虑目标落在多普勒网格外的情况,因此提高重构算法在网格未配准时的稳健性也值得进一步研究。
[1] 洪灵, 戴奉周, 刘宏伟. 一种基于二维运动重构的旋转对称目标拟规则进动参数估计方法[J]. 电子与信息学报, 2014, 36(7): 1538-1544. Hong Ling, Dai Feng-zhou, and Liu Hong-wei. An approach for quasi-regularized precession parameters estimation of rotation symmetric object based on two-dimesional motion reconstruction[J]. Journal of Electronics & Information Technology, 2014, 36(7): 1538-1544.
[2] 刘博, 常文革. 步进调频宽带雷达距离扩展目标频域检测算法[J]. 电子与信息学报, 2013, 35(10): 2481-2486. Liu Bo and Chang Wen-ge. Range-spread target detection of stepped chirp modulated radar in the frequency domain[J]. Journal of Electronics & Information Technology, 2013,35(10): 2481-2486.
[3] 黄培康, 殷红成, 许晓剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 255-256. Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2005: 255-256.
[4] Wehner D R. High-Resolution Radar[M]. Second Edition,Boston, MA: Artech House, 1995, Ch.1.
[5] James D and Taylor P E. Ultra-Wideband Radar Technology[M]. New York: CRC Press, 2001, Ch.1.
[6] Zhu Huan, Chen Yi, and Wang Ning. A novel method of wideband radar signal detection[C]. IEEE 7th International Congress on Image and Signal Processing, Dalian, 2014: 847-851.
[7] Li X, Qiao D, and Li Y. Macro-motion detection using ultra-wideband impulse radar[C]. IEEE 36th Annual International Conference on Engineering in Medicine and Biology Society (EMBS), Chicago, IL, 2014: 2237-2240.
[8] Sakamoto T and Sato T. Exploiting multipath echoes with Capon method for high-resolution ultra-wideband radar imaging using a single omni-directional antenna[C]. IEEE Conference on Antenna Measurements and Applications(CAMA), Antibes Juan-les-Pins, 2014: 16-19.
[9] Conte E, Maio A D, and Ricci G. GLRT-based adaptive detection algorithms for range-spread targets[J]. IEEE Transactions on Signal Processing, 2001, 49(7): 1336-1348.
[10] Perry P R, Dipietro R C, and Fante R L. Imaging of moving target[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188-200.
[11] 高玉祥, 张兴敢, 柏业超. 基于 Keystone变换的高速运动目标检测方法研究[J]. 南京大学学报(自然科学版), 2014, 50(1): 30-34. Gao Yu-xiang, Zhang Xing-gan, and Bai Ye-chao. Research on high-velocity targets detection based on Keystone transform[J]. Journal of Nanjing University (Natural Science),2014, 50(1): 30-34.
[12] 侯庆禹, 刘宏伟, 保铮. 基于 Keystone变换的宽带目标识别雷达杂波抑制[J]. 系统工程与电子技术, 2009, 31(1): 49-53.Hou Qing-yu, Liu Hong-wei, and Bao Zheng. Clutter suppression of wideband target recognition radars based on Keystone transformation[J]. Systems Engineering and Electronics, 2009, 31(1): 49-53.
[13] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2010: 20-45. Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technique[M]. Beijing: Publishing House of Electronics Industry, 2010: 20-45.
[14] Bidon S, Tourneret J Y, Savy L, et al.. Bayesian sparse estimation of migrating targets for wideband radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014,50(2): 871-886.
[15] 杨万海. 雷达系统建模与仿真[M]. 西安: 西安电子科技大学出版社, 2007: 48-73. Yang Wan-hai. Modelling and Simulation of Radar Systems[M]. Xi’an: Xidian University Publishing House, 2007: 48-73.
[16] Rangaswamy M, Weiner D, and Ozturk A. Non-Gaussian random vector identification using spherically invariant random process[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(1): 111-124.
[17] 戴奉周. 宽带雷达信号处理-检测、杂波抑制与认知跟踪[D].[博士论文], 西安电子科技大学, 2010. Dai Feng-zhou. Wideband radar signal processing-detection,clutter suppression and cognitive tracking[D]. [Ph.D. dissertation], Xidian University, 2010.
[18] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[19] Ziniel J and Schniter P. Dynamic compressive sensing of time-varying signals via approximate message passing[J]. IEEE Transactions on Signal Processing, 2013, 61(21): 5270-5284.
[20] Angelosante D, Giannakis G B, and Grossi E. Compressed sensing of time-varying signals[C]. IEEE 16th International Conference on Digital Signal Processing, Santorini-Hellas,2009: 1-8.
[21] Tan X, Roberts W, Li J, et al.. Sparse learning via iterative minimization with application to MIMO radar imaging[J]. IEEE Transactions on Signal Processing, 2011, 59(3): 1088-1101.
方 明: 男,1987年生,博士生,研究方向为认知雷达、空时自适应处理、目标检测.
戴奉周: 男,1978年生,博士,讲师,研究方向为统计与自适应信号处理及其在雷达信号处理和目标检测中的应用.
刘宏伟: 男,1971年生,博士,教授,博士生导师,研究方向为雷达信号处理、雷达自动目标识别等.
王小谟: 男,1938年生,教授,博士生导师,中国工程院院士,主要研究方向为雷达信号处理等。
秦 童: 男,1988年生,博士生,研究方向为目标跟踪、资源优化等.
Detection of Moving Targets for Wideband Radar Based on Joint-sparse Recovery
Fang Ming①Dai Feng-zhou①Liu Hong-wei①Wang Xiao-mo①②Qin Tong①
①(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)②(China Academy of Electronics and Information Technology, Beijing 100041, China)
Range migration is the basic and troublesome problem in moving target detection for wideband radar. To solve this problem, a detection algorithm of moving targets based on joint-sparse recovery is proposed for wideband radar. Firstly, a prewhitening processing is performed to filter the clutter. Then, a jointly row sparse representation of the wideband signals is derived in frequency/slow-time domain,thus the detection problem is solved via joint-sparse recovery. Finally, by using the inverse Fourier transform, the estimation of the targets scenario is achieved. Numerical results are presented to demonstrate the effectiveness of the proposed algorithm.
Wideband radar; Target detection; Range migration; Clutter suppression; Joint-sparse recovery
s: The National Natural Science Foundation of China (61271291, 61201285); Program for New Century Excellent Tallents in University (NCET-09-0630); The Foundation for the Author of National Excellent Doctoral Dissertation of China(FANEDD-201156); The Fundamental Research Fund for the Central Universities of China (2012 HGCX0001)
TN958.92
A
1009-5896(2015)12-2977-07
10.11999/JEIT150442
2015-04-20;改回日期:2015-07-13;网络出版:2015-08-28
*通信作者:戴奉周 fzdai@xidian.edu.cn
国家自然科学基金(61271291, 61201285),新世纪优秀人才支持计划(NCET-09-0630),全国优秀博士学位论文作者专项资金(FANEDD-201156)和中央高校基本科研业务费专项资金资助课题
