多智能体蝙蝠算法在无线传感器中的应用*

尚俊娜，刘春菊，岳克强，李　林

（1.杭州电子科技大学通信工程学院，杭州310018；2.杭州电子科技大学电子与信息学院，杭州310018）

多智能体蝙蝠算法在无线传感器中的应用*

尚俊娜1*，刘春菊1，岳克强2，李林1

（1.杭州电子科技大学通信工程学院，杭州310018；2.杭州电子科技大学电子与信息学院，杭州310018）

针对无线传感器网络（WSNs）节点的定位误差较大的问题，提出了一种新的具有局部搜索能力强的多智能体蝙蝠算法。改进算法中对寻优蝙蝠个体融入多智能体技术，通过邻域竞争合作算子以及自学习过程提高了算法全局搜索能力，避免算法陷入局部最优，加快算法的收敛速度。通过对标准测试函数的仿真，改进算法相比于其他算法，寻优精度和进化效率得到了较大的提高。随后采用多智能体蝙蝠算法求解无线传感节点定位问题，仿真结果表明改进算法减少了测距误差对定位精度的影响，提高了未知节点定位的精度，为无线传感网络节点定位的实际应用提供理论参考。

无线传感网络节点定位；多智能体；蝙蝠算法；定位精度

EEACC:6150，6510Pdoi:10.3969/j.issn.1004-1699.2015.09.025

无线传感器网络节点自身定位至关重要，在军事和民用领域中有着广泛的应用前景，因此，研究无线传感器节点定位十分必要。节点定位有基于测距和非测距两种方式，其中测距定位算法具有定位精度相对较高、通信开销较小等优点，成为当前研究的热点。测距定位［1］包括节点测距和定位两部分，首先通过接收信号强度值（Received Signal Strength Indicator，RSSI）、到达时间（Time of Advent，TOA）、到达角（Angle of Arrival，AOA）［2］等技术测量出待定位节点与信标节点的距离，然后再通过三边测量法、三角测量定位、极大似然估计等算法［3］实现待测节点的位置估计。无线传感器节点定位问题可以转换成一个多约束优化问题，通过智能算法对节点进一步优化来提高定位精度［4-5］，尤其是精度高、容错能力强的算法成为研究的重点。

蝙蝠算法（Bat Algorithm，BA）具有模型简单［6］，寻优精度高等特点，该算法逐渐成为研究的热点。文献［7］将无线传感网节点定位的问题通过数学模型转换为节点优化问题，针对最小二乘算法节点定位的不足通过BA进行优化，节点定位精度得到提

项目来源:浙江省自然科学基金青年基金项目（LQ13F010010）；浙江省重点科技创新团队项目（2013TD03）

1　MA-BA算法

1.1标准BA算法基本原理

蝙蝠算法［10］是一种群体智能随机搜索优化算法，蝙蝠个体利用自身回声定位能力，通过所发出的脉冲频率、响度、脉冲发射的频度的变化来捕获猎物。在实际的优化算法中，每只蝙蝠为搜索解空间的一个点，由适应度函数来决定蝙蝠位置的优劣。蝙蝠的每一次有效飞行就是BA算法的一次迭代更新。在t时刻，d维空间中，蝙蝠个体的飞行速度vi和空间位置xi的更新公式如下:

式中:fi是第i只蝙蝠个体所发出的的脉冲频率，且fi∈［fmin，fmax］，β∈［0，1］是均匀分布的随机向量。x*是该时刻下的全局最佳位置。个体更新后以发射脉冲的频度ri为门限值随机选取个体进行最优解扰动:

Xnew=x*+σAt（4）

σ为［-1，1］上的随机数值，At为某一个时间中所有蝙蝠个体平均求得的响度。

蝙蝠个体在寻找猎物的过程中，一开始发射脉冲的频度r较低，脉冲响度A较大，一旦发现猎物，就逐渐减小脉冲音强和增大发射脉冲的频度。A与r在发现猎物后的更新公式如下:

1.2MA-BA算法

标准BA算法中蝙蝠个体由于局部搜索能力不强容易陷入局部最优解，我们从智能体系统的角度出发，把蝙蝠算法中的个体作为一个具有局部感知、竞争协作和自学习能力的智能体，通过智能体与环境以及智能体间的相互作用达到全局优化的目的［11］，据此本文提出基于多智能体的蝙蝠算法。通过将BA算法中的个体视为多智能体系统（Multi-Agent System，MAS）中的智能体，借助智能体的基本原理和操作，蝙蝠个体在搜索空间能够由自身的局部搜索逐步扩散到全局搜索，并通过自学习不断优化自身，寻优迅速跳出局部极值避免早熟，更快更准寻得全局最优解。通常每个Agent具有以下特征:

①单个Agent的定义

在MA-BA算法中，每一个Agent相当于BA算法中的一个蝙蝠个体，可以感知所在的局部环境，实现与邻域Agent的竞争合作以及自身学习过程，根据环境改变自己同时也改变所处环境。每个个体位置在解空间中的优劣是由被优化的目标函数所决定，因此每一个Agent的目的是在搜索空间内拥有局部最小适应度值。

②Agent网格环境

由于每一个Agent相当于BA算法中的一个个体，MAS体系结构可以借鉴PSO的拓扑结构。本文同样选取了结构简单稳定的Von Neuman结构，如图1所示。每一网络节点就表示MA-BA算法中的一个Agent，即一个蝙蝠个体，而网络节点的位置坐标就表示Agent在网格中固定位置。每一网格节点除了包含自身节点固定位置坐标以外还包括蝙蝠个体在解空间的位置和速度。图1中共有m×n个Agent，即MA-BA算法中个体的总数。

图1　Von Neumann结构图

③Agent的局部环境

Agent的局部环境是由每个Agent的所有邻居构成即邻域。假设 Ai，j表示Von Neuman结构中位于位置（i，j）的智能体，那么它的邻域Agent可以由式（7）被定义:

④Agent的行动策略

在MA-BA算法中，每一个Agent与其邻域的智能体进行竞争合作，假设Agent Ai，j在解空间的位置向量为（a1，a2，…，aN），其邻域个体可以有式（7）唯一确定。设Mi，j=（m1，m2，…，mN）为其邻域中具有最小适应度值的最优个体，若Ai，j与Mi，j满足下式（8），则说明Mi，j在解空间中的位置优于Ai，j，对Ai，j在解空间中按照式（9）进行重新赋值。若不满足式（8），则保留Ai，j在解空间中的位置。f（Mi，j）≤f（Ai，j）（8）

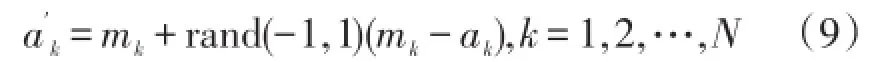
从式（9）知，Ai，j解空间位置更新后不仅保留了自身有用信息同时吸收了最优邻居Mi，j的有用信息，使其适应度值进一步减小。通过Agent的行动策略，Agent自身信息在Agent局部环境中的逐步传递，同时与全局最优Agent进行信息交换，通过Agent之间的信息的交流对其行动策略进行修正，增强了局部搜索能力和算法寻优效率。

⑤Agent的自学习过程

要达到MAS的适应性，智能体的自我学习能力是不可缺少的［12］。为了防止寻优算法的计算复杂度过大，不利于算法的计算效率，我们一般选取较小的搜索半径sR构建智能体网格，在小范围内扩展全局最优个体搜索空间。通过这个网络和已知的信息进行局部寻优，用寻找到更好的解来替换原来解空间中位置。通过自学习过程，最优个体更可能找到全局最优位置，从而可以指导其他个体尽快找到最优解，提高进化效率。

假设Agent Li，j在解空间中的位置为Li，j=（a1，a2，…，aN），构造一个类似图1结构的网格，大小为n=sLsize×sLsize。在该Agent局部环境中的个体记为sAi′，j′，i′，j′∈｛1，2，…，n｝，每一sAi′，j′有式（10）进行赋。

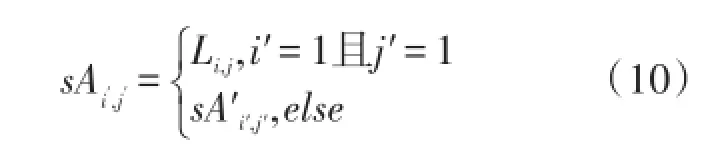
式中:k=1，2，…，N，sR为智能体能够进行搜索到的空间范围，一般取值范围为［0，1］。由于在该MAS结构中，Agent个体较少，能快速地将信息传递到整个环境，通过设定的迭代次数完成最优解替换。

2.3MA-BA算法步骤

①按照图1的形式构造Lsize*Lsize的Agent的生存环境，初始化各个参数以及Agent在解空间中位置x和速度v。

②计算种群每个Agent的适应度值Fitness（i），根据式（7）求解出Agent Ai，j的邻居，在所有邻居个体中寻找适应度值最小的最优邻居Mi，j，并记录全局最优解Agent（x*）。

③根据式（8）、式（9）进行邻居间竞争合作操作，并改变失败个体在解空间中的位置，重新计算所有Agent适应度值Fitness（i），并记录全局最优Agent（x*）和对应的适应度值 f（x*）。

④通过式（1）～式（3）更新每个Agent解空间中的位置x和速度v，并记录更新后的个体的适应度值为Fnew。

⑤通过条件rand1＞r（i）来判断是否进行最优解扰动来产生新解。如果满足条件，则根据式（4）产生局部解来替代当前解，并替换当前适应度值。如果不满足则跳过该步。

⑥如果更新后的蝙蝠个体满足条件Fnew＜Fitness（i）&rand2＜A（i），则接受该新解，替换个体原来的位置状态并根据式（5），式（6）开始脉冲响度A和发射脉冲的频度r更新。如果不满足条件表示这该个体的位置更新不成功，跳过该步。

⑦如果接受的新解对应的适应度值Fnew＜f（x*），则替换全局最优解及其对应的最小适应度值。否则跳过该步。

⑧对全局最优解Agent（x*）重新构造搜索半径为sR的小规模网格，按照式（10）、式（11）进行自学习过程操作，寻找适应度值更小的个体Agent（x′*）替换原来Agent（x*）。

⑨若算法搜索到最大迭代次数或者要求的精度则跳出循环输出结果，否则返回步骤2）继续搜索。

1.3MA-BA算法性能测试

为了验证本文提出的MA-BA算法的性能，选取了4个标准测试函数进行仿真测试，并与文献［14］所改进的具有混沌搜索策略的蝙蝠算法（Chaos bat algorithm，CBA）、标准BA算法和基本PSO算法进行对比。

1.3.1参数设置

蝙蝠算法中各种参数设置目前没有明确的理论依据，因此本文所设置的参数值根据反复实验获得的经验值来确定。MA-BA算法中:个体总数N= 64，网格Lsize×Lsize=8×8，维数d=30，搜索脉冲频率范围［0，100］，最大脉冲频度r=0.5，最大脉冲音强A=0.25，脉冲音强衰减系数γ=0.95，脉冲频度增加系数 α=0.05，自学习半径sR=4，迭代sGen=10。CBA、BA算法中各个参数与MA-BA算法保持一致。PSO算法采用文献［15］中所提出的线性减少的惯性权重:Wmax=0.9，Wmin=0.4；学习因子:C1=0.5 C2= 1.4962。上述算法最大迭代次数均为200次，每种算法独立运行30次。其中，PSO表示基本粒子群算法，BA表示基本蝙蝠算法，CBA表示具有混沌搜索策略的蝙蝠算法，MA-BA表示多智能体蝙蝠算法。

1.3.2标准测试函数

实验选取的测试函数介绍如下:

Sphere函数该函数为非线性连续单峰函数，计算简单，容易实现，用于检验算法的精确度。

②Rosebrock函数:

搜索空间为［-2.048，2.048］；

Rosenbrack函数是单峰连续函数，其极小点所在的山谷易于找到，但取值区间走势平坦，很难收敛到全局最优点，是测试算法全局收敛性能的经典函数。

③Griewank函数

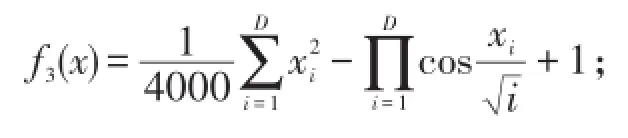
搜索空间为［-600，600］；

Griewank函数是多峰多极值函数，有众多局部极值，种群极易陷入局部极值中，主要用来评价算法的探索、开发能力。

④Ratrigin函数:

搜索空间为［-5.12，5.12］；

Rastrigrin函数为多极值函数，加入的余弦函数使函数的优化更为复杂，在解空间内存在大约10 d个（d为解空间维数）局部极小点，极易陷入局部最优。

1.3.3仿真效果分析

图2　标准测试函数寻优曲线图

图2显示了以上4个标准函数的寻优曲线，其中f1、f2、f3理论上全局最优解为:min（f（0，0，…，0））=0。f4的全局最优解min（f（1，1，…，1）=0，规定当优化精度达到10-6时，算法成功找到全局最优解。对于具有混沌搜索策略的CBA算法，采用对精英个体进行混沌优化，然而对于复杂的问题其寻优效果并没有较大提高。MA-BA算法则是在每个个体所处的局部环境中通过竞争合作寻找最优个体，具有较强的适应能力和搜索能力，同时最优个体具有自学习能力可以有效引导全局进化方向加快算法寻优速度。从图2可以看出，对于单模的Sphere函数，四种算法均能寻找到最优解，但是MA-BA算法的优化精度比其他三种算法提高很多，寻优效率大幅度提高。对于Griewank函数，Rosenbrack函数和Rastrigrin函数的寻优曲线，MA-BA算法的优化性能均明显优于其他算法，不仅寻优精度高而且收敛速度快，在较少的迭代次数内达到所设定的最优解，体现了MA-BA算法由于多智能体技术的融入，使得每个Agent局部搜索能力大大增强，可以跳出局部最优避免早熟。

在标准函数的测试中，对于单模函数，以其理论最优值的1‰为标准，多模函数以最优理论值5‰为标准，如果最小适应度值小于以上标准说明该算法取得了正确解，用寻优成功率来表示算法的稳定度。表1中是图2中各个函数的测试结果，解空间为30维，取30次寻优值结果进行平均，其他仿真参数如上文中所设置。由表1可知，无论是病态单峰函数还是具有较多局部极值的多峰函数，相比CBA、BA和PSO，MA-BA算法的寻优成功率较高，体现了算法的鲁棒性。平均最小适应度值很接近于理论值最优解，说明MA-BA算法的局部搜索能力比较强，能跳出局部最优解，使算法具有较高的优化精度。

表1　标准函数测试结果

2　MA-BA算法在无线传感网络节点定位中的应用

下面将MA-BA算法用于无线传感器网络定位的问题上来验证本算法在最优解寻优精度上的性能。对于传感器定位问题，由于传感器节点上自带的RSSI指示功能，采用基于RSSI算法测距并不增加硬件设备成本［16］，所以本算法建立在RSSI测距的基础上对定位计算进行优化。在仿真研究中，以平均定位误差AVE作为定位误差大小的评判标准，为了便于比较，所有定位误差均为绝对误差，其公式如下:

其中:（x，y）为预测位置，（xi，yi）为实际位置，M为已知节点的总数。

2.1无线传感网络节点定位数学模型

设传感器网络有M个已知节点，N个未知节点。M个已知节点坐标分别为（x1，y1），（x2，y2），…（xM，xN），对于任意一个未知节点D（x，y），测得到各个锚节点的距离分别为d1，d2，…，dM那么，未知节点的位置可以有方程求解出:

在实际的测距中总是存在误差，所以定位问题就转化为函数

求最小值的优化问题。由上一节可知，利用MA-BA算法求解优化问题时，该算法具有较强的局部搜索能力和较高的寻优进化效率，能避免个体陷入局部最优解，具有较高的优化精度和收敛速度。将该方法用于函数 f（x，y）寻找最优解的问题上，可以减小测距误差的影响，提高未知节点的定位精度。

2.2仿真分析

仿真实验以MATLAB 7.0为平台，节点的通信半径设置为10 m，30个传感器节点随机分布在30 m×30 m的正方形区域内，测距误差在10%以下，锚节点个数为5，仿真算法中参数设置为上文1.3.1节所示，最大迭代次数为200次，每一个节点定位预测值选取20次平均值。分别用MA-BA算法和文献［14］中采用CBA算法进行节点定位结果进行对比，结果如图3、图4所示。

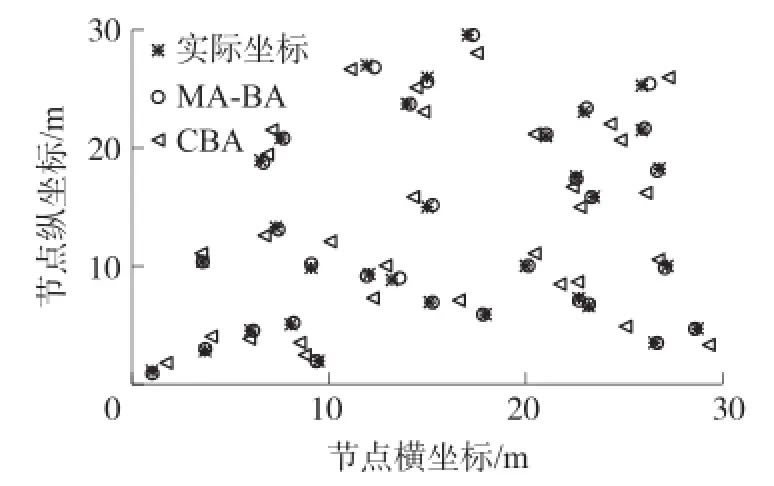
图3　未知节点预测比较图

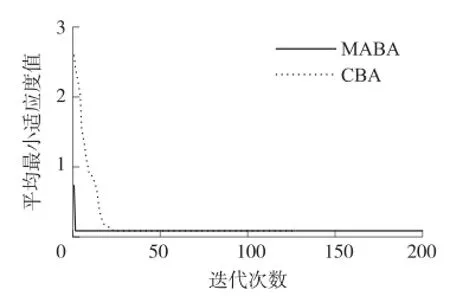
图4　两种算法的平均寻优曲线

图3是对30个未知节点预测位置的仿真，由图3可知，BA算法预测位置与实际位置有一定的差距，定位精度不是很理想。MA-BA算法预测位置与节点实际位置几乎完全重合，绝对误差值较小，显示了Agent个体在寻优方面具有较强的局部搜索能力和全局寻优能力，减少了测距误差对定位精度的影响。图4是在10%的误差范围内图3中30个节点的平均优化曲线，从图中可知，MA-BA算法的优化精度和收敛速度明显好于BA算法，多智能体技术使算法效率得到了很大的提高。

在基于RSSI测距定位的算法中，测距误差对未知节点定位精度影响很大，在不同的测距误差下MA-BA，CBA，BA，PSO的平均定位误差如图5所示。其中锚节点个数为10。从图5可知，在5%内的测距误差下，MA-BA，CBA，BA均能达到较高的精度，但是随着测距误差的增加，与文献［7］中结果相比较，MA-BA算法由于个体间的竞争合作及自学能力，增强了局部和全局搜索能力有效降低了测距误差对定位精度的影响，使其性能明显优于BA算法。当测距误差在15%到30%之间时，CBA，BA和PSO对测距误差比较敏感使得平均定位误差明显增加而MA-BA算法的整体曲线整体变化比较平稳，误差忍受力较强性能比较强，算法性能比较稳定。

图5　测距误差对定位性能的影响

图6是不同算法在15%的测距误差内不同锚节点个数情况下平均定位误差曲线图。从图中可知，MA-BA算法可以利用较少的锚节点实现高精度节点位置预测，整条曲线变化比较缓慢，利用MA-BA算法具有寻优精度高的优势来补偿定位精度对锚节点个数的依赖，而BA算法和PSO算法则对锚节点个数依赖性较强，平均定位误差变化比较剧烈。虽然CBA算法曲线变化缓慢但是整体上定位精度没有MA-BA算法的精度高。因此在相同的定位精度下MA-BA算法可以大大节省定位成本，有较大的应用前景。

图6　锚节点个数对定位性能的影响

3　结束语

针对基本蝙蝠算法中蝙蝠个体局部搜索能力不强易陷入局部最优解的缺点，提出了基于多智能体的蝙蝠算法，对蝙蝠个体赋予局部感知、竞争合作和自我学习的能力，通过个体Agent之间的相互作用增强了蝙蝠个体局部和全局的搜索能力，使个体迅速跳出局部最优解避免早熟，提高了算法的进化效率，能更快更迅速的找到全局最优解。通过对标准测试函数的仿真，验证了MA-BA算法具有高精度的全局寻优能力以及收敛速度快的优点。将多智能体蝙蝠算法应用到无线传感网络节点定位中，仿真结果表明MA-BA算法不仅对测距误差的忍受能力较强，而且可以在较少的锚节点个数下实现精确定位，节约定位成本。

［1］ Patwari N，Ash J N，Kyperountas S，et al.Locating the Nodes:Cooperative Localization in Wireless Sensor Networks［J］.IEEE Signal Processing Magazine，2005，22（4）:54-69.

［2］ Niculescu D，Bath B.Localized Positioning in ad-hoc Networks［J］.IEEE International Workshop on Sensor Network Protocols And Applications，Publish Elsevier Ad Hoc Networks，2003，1 （23）:421-150.

［3］ 程海军.基于RSSI的无线传感网络定位算法的改进研究［D］.重庆:重庆理工大学计算机工程与科学学院，2013:29-32.

［4］ 李牧东，熊摇伟，梁摇青.基于人工蜂群改进算法的无线传感器网络定位算法［J］.传感技术学报.2013，26（2）:241-245.

［5］ 曹欲晓，严奎，徐金宝.一种最优锚节点集合上的两重粒子群优化DV-HOP定位算法［J］.传感技术学报.2015，28（3）:424-430.

［6］ Tsai P W，Pan J S，Liao B Y，et al.Bat Algorithm Inspired Algorithm for Solving Numerical Optimization Problems.Applied Mechanics and Materials，2012.

［7］ 王战备.基于蝙蝠算法的无线传感网络节点定位［J］.计算机工程与应用，2014，50（11）:90-94.

［8］ 谭爱平，陈浩，吴伯桥.基于BADV-Hop的无线传感器网络节点定位方法［J］.计算机工程与应用，2014，50（17）:125-129.

［9］ 康琦，汪镭，吴启迪.群体智能与人工生命［J］.模式识别与人工智能，2005，18（6）:689-697.

［10］Yang Xinshe.A New Meta-Heuristic Bat Inspired Algorithm［M］// Nature Inspired Cooperative Strategies for Optimization.Berlin: Springer-Verlag，2010:65-74.

［11］赵波，曹一家.电力系统无功优化的多智能体粒子群优化算法［J］.中国电机工程学报，2005，3（5）:1-7.

［12］陈自郁.粒子群优化的邻居拓扑结构和算法改进研究［D］.浙江:浙江大学，2009.

［13］肖琨，黄挚雄.多智能体粒子群算法在配电网络重构中的应用［J］.计算机工程与应用，2010，46（8）:221-2244.

［14］刘长平，叶春明.具有混沌搜索策略的蝙蝠优化算法及性能仿真［J］.系统仿真学报，2013，25（6）:1183-1188.

［15］Shi Y，Eberhart R.A Modified Particle Swarm Optimizer［C］//Proceedings of IEEE International Conference on Evolutionary Computation.Anchorage，USA:IEEE，1998:69-73.

［16］方震，赵湛，郭鹏，等.基于RSSI测距分析［J］.传感技术学报，2007，20（11）:2526-2571.

尚俊娜（1979-），女，河南开封人，副教授，博士，主要研究方向为通信信号处理、智能算法；

刘春菊（1988-），女，河南许昌人，硕士研究生，主要研究方向为智能算法；

岳克强（1984-），男，河南信阳人，讲师，博士，主要研究方向为进化计算、通信信号处理。

The Multi-Agent Bat Algorithm Applied to Wireless Sensor Networks*

SHANG Junna1*，LIU Chunju1，YUE Keqiang2，LI Lin1
（1.College of Telecommunication Engineering，Hangzhou Dianzi University，Hangzhou 310018，China: 2.College of Electrical and Information Engineering，Hangzhou Dianzi University，Hangzhou 310018，China）

In order to solve the node location error in wireless sensor networks（WSNs），this paper proposes a new multi-agent bat algorithm，which possesses favorable local searching ability.In the proposed algorithm，the bat individual is a agent，which could compete and cooperate with its agent neighbor areas to improve the efficiency of local searching.In this way the multi-agent bat algorithm（MA-BA）could avoid the algorithm into a local optimum and increase the convergence speed.Simulation results for standard test functions indicate that the proposed algorithm remarkably improves the global optimizing ability and evolutionary efficiency compared to other algorithms.Through implementing the MA-BA to node location prediction，the precision of the unknown node location could be improved due to decreasing the ranging error and has a certain significance to practical application of wireless sensor network node localization.

WSNs node localization；multi-agent；bat algorithm；accuracy

TP393

A

1004-1699（2015）09-1418-07

2015-04-02修改日期:2015-06-29高。文献［8］将BA算法与DV-Hop算法相结合，在DV-HOP的第三阶段利用蝙蝠算法代替最小二乘法来计算未知节点的坐标，降低了平均跳距导致的定位误差，定位精度有所改善。但基本BA算法存在易陷入局部最优、发生过早收敛、后期收敛速度较慢等问题［9］其性能有待提高。本文针对基本蝙蝠算法的缺点，提出了基于多智能体蝙蝠算法（Multi-Agent Bat Algorithm，MA-BA）。建议算法中通过采用基本蝙蝠算法的拓扑结构来构建多智能体的体系结构，将每一个蝙蝠个体作为一个智能体，通过与邻域的智能体竞争、合作以及自我学习，从而避免算法陷入局部最优，提高算法的收敛速度，个体的更新机制减少了算法不可行解的产生，提高了算法效率。通过对标准测试函数仿真，改进的MA-BA算法在寻优精度上相比于基本BA算法有较大提高，同时将其应用在无线传感器节点定位的应用中，节点的平均定位误差相对较低，获得了比较理想的节点定位结果。