众包竞赛中众包方的反馈策略

2015-08-17葛如一张朋柱

系统管理学报 2015年6期

葛如一，张朋柱

（1.上海商学院信息与计算机学院，上海 200235；2.上海交通大学安泰经济与管理学院，上海 200030）

众包是指“一个公司或机构把过去由员工执行的工作任务，以自由自愿的形式外包给非特定的（而且通常是大型的）大众网络”1）引自维基百科。这是一种独特的外包模式，主要在互联网上进行，其价值来源于互联网背后隐藏着的庞大人力资源。众包活动存在多种组织形式来选择和激励合适的参与者［1-2］，众包竞赛是其中一种常见的组织形式：由众包方在互联网上公布一个任务并给出相应的奖金，所有感兴趣者均可参加竞赛完成该任务，其中表现最佳者获得奖金。著名的众包竞赛的例子包括Netflix公司出资100万美元为其电影推荐系统悬赏最佳改进方案、Google公司出资1 000万美元悬赏让世界变得更美好的创意等。除了这些由知名企业自己组织的众包竞赛外，还有大量企业和个人通过专业的众包平台来组织众包竞赛。例如，在InnoCentive.com上，许多企业以竞赛的形式发布具有挑战性的技术难题，吸引世界各地的科学家和研究者来解决；在Elance.com和Taskcn.com上，大量的中小企业和个人以竞赛的形式众包各类设计工作等。

1 众包竞赛中的众包方反馈

近年来，随着众包竞赛的迅速发展，有关众包竞赛的研究也开始日渐增多。其中，大多数的研究均将众包竞赛看作一种无反馈竞赛，即在竞赛过程中，参赛者不会得到有关自己表现的反馈信息。然而，在实际的众包竞赛中，众包方往往会在竞赛过程中和参赛者保持沟通，对参赛者的表现给予反馈。很多专业的众包平台甚至还会提供一些专门的软件工具来帮助众包方及时给予反馈，例如InnoCentive.com为每个竞赛开辟专门的项目空间供众包方和参赛者交流；Elance.com为每个竞赛提供工作室以及专门的即时通讯工具来加强双方的沟通。

Yang等［3］最先对众包竞赛中存在的反馈现象进行了研究。他们指出，众包竞赛的特点之一就是众包方可以在竞赛的过程中向参赛者就其表现提供反馈，从而鼓励参赛者投入更多的努力，并且帮助参赛者提高其努力的效率。他们还专门在一个众包平台上组织了一次众包竞赛，来考察众包方给予的反馈对于参赛者行为的影响。他们在市场上发布了一个设计网站标志的任务，在为期15天的竞赛过程中，共吸引了46位用户参赛，最终获得了34份完整的作品。在竞赛刚开始时，每位参赛者都提交了一份作品。研究人员向其中的38位参赛者提供了反馈意见，随后收到了43份修改作品，反馈的回复率达到100%，平均每个反馈意见带来1.13个修改作品。而最终的获胜者共获得4次反馈意见，对作品进行了5次修改。Yang等认为与无反馈的情况相比，众包方给予参赛者反馈可以明显增加参赛者为完成任务所付出的努力。

Yang等进一步指出，参赛者在收到反馈后愿意再追加努力修改作品的行为可以用期望收益折扣理论［4-7］来解释。在竞赛中，参赛者的期望收益等于奖励金额乘以其可能获奖的概率。当获得众包方的反馈后，参赛者会将众包方愿意提供反馈理解为众包方对其作品比较青睐，从而提高对作品获奖概率的预估，其期望收益也就随之提高。只要期望收益能够补偿他的总努力成本，参赛者就会愿意追加努力，因为如果他不追加努力则很有可能无法获奖，那么他之前付出的努力也就无法获得补偿。

Yang等的上述解释是容易理解的，但是值得注意的是，他们的研究存在一个前提：参赛者事先并不知道众包方会在竞赛过程中给予反馈。本文将这种反馈称之为事先隐瞒的反馈。换句话说，在竞赛开始前，众包方有意或无意地隐瞒了这是一个有反馈的竞赛。在这种情况下，参赛者的行为不具有整体策略性，因此会损失一部分的收益，而众包方则会获得额外的收益。反之，如果众包方事先声明在竞赛中会给予反馈，那么参赛者将采取具有整体优化性质的策略行为，此时，众包方是否还能获得额外的收益就不一定了。即使众包方没有预先声明，但是如果参赛者在一开始就预估到众包方会在竞赛中给予反馈，那么他们采取的策略将等同于在事先声明的有反馈竞赛中采取的策略。

由于在几乎所有的众包平台中，平台运营方对于众包方的反馈策略都没有明确规定，故众包方可以自由选择反馈策略。主要的反馈策略有3种：无反馈、事先声明的有反馈和事先隐瞒的有反馈。虽然已有不少关于竞赛中竞赛组织者（等同于这里的众包方）反馈策略的研究，但是这些研究只考虑了无反馈策略和事先声明的有反馈策略，忽视了事先隐瞒的有反馈策略。事先隐瞒的有反馈策略之所以被忽视是因为在一个供需双方相对固定的市场，这种策略不太可能被重复采用。众包方采用一两次这种策略后，参赛者很快就能吸取教训，以后无论众包方是否事先声明，参赛者都会采用有反馈竞赛策略来应对。然而，众包竞赛的市场中存在着大量的众包方和参赛者，并且不断有新的无经验的用户加入进来，这就使得事先隐瞒的有反馈策略可以一直存在，成为众包方可选的策略之一。

本文对上述众包竞赛中众包方可选的3种反馈策略进行分析，比较这3种策略所导致的众包方和参赛者收益，说明众包方在不同情况下应如何选择反馈策略。

2 相关研究

Lizzeri等［8］和Aoyagi［9］比较了当参赛者同质（参赛者能力相同）时，两种不同的反馈策略——完全反馈策略和无反馈策略的优劣。所谓完全反馈策略就是指无论参赛者的表现情况如何，竞赛组织者都将给予反馈，而无反馈策略就是指无论什么情况，竞赛组织者都不会给予反馈。这里的反馈信息主要是指参赛者的相对表现情况，如在所有参赛者中的排名，与其他人有多少差距等。他们的研究结果均显示，选择何种反馈策略取决于参赛者成本函数的形式，具体来说，如果参赛者的边际成本是凹的，那么完全反馈策略最优；如果参赛者的边际成本是凸的，那么无反馈策略最优。

Goltsman等［10］的研究同样假设参赛者同质，但是包括了更为丰富的反馈策略。竞赛组织者可以根据参赛者不同的表现情况来决定是否提供反馈，例如，在参赛者均表现良好的情况下提供反馈，或者在部分参赛者表现良好、部分参赛者表现不佳的情况下提供反馈等。他们的研究结果显示，当参赛者均表现不佳的情况下提供反馈是竞赛组织者的最优策略。

Gershkov等［11］则研究了在参赛者同质的有反馈竞赛中，竞赛组织者应该如何设置每阶段评分的比重。每一阶段竞赛结束后竞赛组织者方将比较所有参赛者的表现并将比较后的评分情况反馈给参赛者，每一阶段的评分都会对最终的评分产生影响，而不同阶段的评分可以有不同的影响系数。竞赛组织者的最优策略是将最后阶段评分的影响系数设置为最大，并且参赛者在第1阶段的努力对于最终产出的影响越大，最后阶段评分的影响系数就应该设置得越大。

与以上研究均假设参赛者同质不同，Ederer［12］研究了当参赛者异质时完全反馈策略和无反馈策略的优劣。这里的异质参赛者是指参赛者具有不同的能力。Ederer证明了如果参赛者的产出由其能力参数和其投入相加而得，即能力参数对于其边际投入的价值没有影响，那么完全反馈策略和无反馈策略无差异；如果参赛者的产出由其能力参数和其投入相乘而得，即能力参数对于其边际投入的价值有直接影响，那么，当参赛者的成本函数为二次函数，影响产出的随机因素满足标准分布条件时，完全反馈策略优于无反馈策略。

由于在众包竞赛中，参赛者不太可能是同质的，故本文的研究与Ederer相同，假设参赛者为异质，并且其产出由其能力参数和其投入相乘而得。但不同的是，在本研究中参赛者的产出不受随机因素的影响，因此，本研究可看作是Ederer的补充。

上述所有研究基本上都假设竞赛组织者在竞赛开始前就声明了自己的反馈策略，并且在竞赛中严格执行该策略。Aoyagi［9］虽然提到竞赛组织者在某些情况下很有可能偏离预先声明的反馈策略，但是并未对此做进一步的分析。然而正如上节中所提到的，在众包竞赛中，众包方并不一定事先声明自己的反馈策略。因此，本文除了讨论众包竞赛中完全反馈策略和无反馈策略的优劣外，还将对事先隐瞒的反馈策略加以讨论。

在本研究中，众包方给谁反馈以及反馈什么信息与以往的研究也有所不同。在以往的研究中，参赛者人数不多，最常见的是两人竞赛。众包方会对所有的参赛者给予反馈，反馈的内容主要是参赛者的相对表现情况。而在众包竞赛中，参赛的人数很多，众包方不太可能对所有的参赛者都给予反馈，而是会选择较有可能获胜的参赛者给予反馈，以激励其做进一步的努力。另外，为了避免让参赛者了解到对手的成本信息，众包方一般直接对于作品给出评价，很少会对反馈作品进行比较。例如，在商标设计类任务中，众包方会对于有较大获胜可能的作品进行反馈，就作品本身提出一些修改意见，而不会将两幅作品加以比较分析其优劣。而对于参赛者来说，众包方的反馈带给他们的最重要信息是如果他们继续努力将有希望赢得竞赛。因此，本文将有反馈的竞赛看作是一个初赛-复赛的两阶段竞赛。在初赛结束时，众包方选择若干参赛者给予反馈，收到反馈的参赛者相当于进入复赛，未收到反馈的参赛者则被淘汰出局。这与传统的“淘汰赛”模式［13-15］很相似，所以本研究借用了淘汰赛模型作为分析的基础。本文反馈竞赛模型与Moldovanu等［15］的淘汰赛模型的区别在于：后者中的参赛者在初赛阶段被分为若干小组，然后各小组的优胜者进入复赛；而本文模型中的参赛者在初赛阶段并不分组，所有参赛者中表现最好的几位参赛者将获得反馈进入复赛。相比之下，本文的模型更符合众包竞赛的实际情况。

此外，本文考虑了两种不同的众包方收益类型：①等于所有参赛者的努力总和；②等于所有参赛者中的最大努力水平。这两种众包方收益类型在众包竞赛中都存在，前者主要是一些集思广益或产品营销竞赛，后者则包括研发竞赛、设计竞赛等。下面将对不同反馈策略下参赛者和外包者的收益进行分析。

3 不同反馈策略下的竞赛模型

3.1 无反馈竞赛模型

首先讨论无反馈竞赛模型。所谓无反馈竞赛就是指在竞赛过程中众包方不给参赛者任何反馈。本文将有反馈竞赛看作是一个初赛-复赛的两阶段竞赛，那么无反馈竞赛就相当于一个单阶段的单奖金竞赛。假设有一个奖金额为M的众包竞赛，共有n个人参赛，参赛者i付出努力xi，产生成本cixi，其中ci＞0为参赛者的能力参数，反映了参赛者的能力类型，较低的ci意味着参赛者i有较高的能力。ci∈［m，1］，并且服从分布函数F，F具有连续的概率密度f＞0。为了避免由零成本而导致的无穷努力情况，假设m严格为正。ci为参赛者的私人信息，F和f为公共信息。努力水平最高的参赛者赢得奖金。参赛者的问题是选择合适的努力水平以最大化自己的效用，即

其中，pi为参赛者i获得奖金的概率。根据文献［15］中的推论1可知，在单阶段竞赛中参赛者的努力水平2）F（1，n—1）为随机变量C（1，n—1）的分布函数，C（1，n—1）为在随机选取的n—1个能力参数中最小的能力参数值

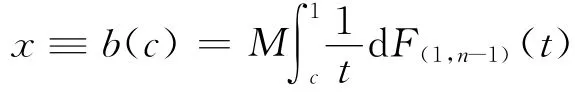
如果众包方的收益等于所有参赛者的努力总和，则众包方的收益为

如果众包方的收益为参赛者的最大努力，则众包方的收益为

其中：下标nofd表示无反馈；上标T表示总努力水平；H表示最大努力水平。

3.2 事先声明的有反馈竞赛模型

事先声明的有反馈竞赛相当于一个两阶段的“淘汰赛”。首先，众包方声明这是一个有反馈的竞赛，最终的优胜者将获得奖金M。在参赛者首次提交了任务成果后，第1阶段竞赛完成。众包方会对表现靠前的k位参赛者给予反馈。参赛者收到反馈就意味着进入了第2阶段竞赛。然后，由第2阶段中表现最好的参赛者赢得奖金。假设在该模型中参赛者的生产函数、人数和能力分布条件与无反馈竞赛模型中的条件相同。

（1）参赛者的努力水平和预期收益。由于众包方事先声明，故参赛者在竞赛开始前就知道众包方会给予反馈，他将以博弈论中的倒推法来决定自己的努力水平。首先，第2阶段竞赛是从众包方给予反馈的k位（k＜n）参赛者中选出一位优胜者的竞赛，优胜者获得全额奖金M。由于第2阶段中的k位参赛者是从n位参赛者中优选而来的，假设k位参赛者的能力分布函数为G，则。将第2阶段竞赛看作一个单阶段单奖金竞赛，参照单阶段单奖金竞赛中参赛者的努力水平，可得参赛者在第2阶段的努力水平

3）因为U2（c）是c的递减函数，所以该等式才成立

参赛者在第1阶段的奖励等同于他在第2阶段可获得的预期收益，即

注意到，U2（c）是c的递减函数，即c越小（能力越大）的参赛者在竞赛第2阶段可获得的收益越大。第1阶段的竞赛是一个从n位参赛者中选拔出k位优胜者的竞赛，并且每位参赛者可能获得的奖金等于参赛者在第2阶段的预期收益。将第1阶段的竞赛看作是一个单阶段多奖金的竞赛，根据文献［15］中的推论1可知，第1阶段的努力水平

（2）众包方的收益。

①收益为努力总和。如果众包方的收益为所有参赛者在整个竞赛过程中的努力总和，则众包方的收益为

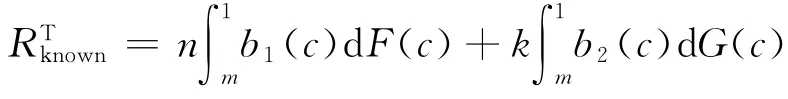
因为U2（c）是c的递减函数，易知b1（c）也是c的递减函数，这就意味着前k位能力高的竞赛者会进入复赛。又因为b2（c）也是c的递减函数，所以，能力最高的参赛者会成为最终的优胜者，这与无反馈竞赛的结果一致，根据收益等价定理4）收益等价定理的具体描述可参见Riley等［16］，众包方在事先声明反馈竞赛中的收益应等于其在无反馈竞赛中的收益，即

②收益为最大努力。如果众包方的收益为所有参赛者中的最大努力水平，即获胜者的努力水平，则众包方的收益为

由2个组成项相加而得，比较的第2项与，由于G（1，k—1）（t）＞F（1，n—1）（t），故可得

3.3 事先隐瞒的有反馈竞赛模型

虽然有反馈竞赛相当于一个两阶段的“淘汰赛”模型。但是，如果众包方事先隐瞒会给予反馈，那么在竞赛的第1阶段，参赛者就很有可能将竞赛看作是一个单阶段单奖金的竞赛，并据此做出相应的努力，直到众包方在竞赛过程中给出反馈，参赛者才会意识到这是一个有反馈竞赛，但此时在第1阶段付出的努力已经无法撤销，只能在此基础上继续追加努力。

（1）参赛者的努力水平和收益。如果众包方事先隐瞒，那么参赛者在竞赛开始时并不知道在竞赛中众包方会给出反馈，在竞赛的第1阶段，参赛者会以为这是一个单阶段竞赛。根据Moldovanu等［15］的推论1可知，参赛者会给出努力水平

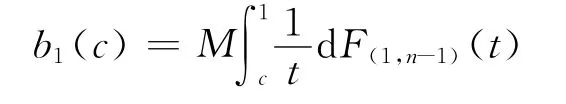
接着，众包方选出k位努力水平靠前的参赛者，给予反馈，那么就相当于开始了一个新的竞赛，在该竞赛中每位参赛者的奖励为第1阶段竞赛的预期收益，而参赛者的能力类型分布函数则为G。U1（c）是c的减函数，因此，参赛者在第2阶段的努力水平

（2）众包方的收益。

①收益为努力总和。U1（c）是c的递减函数，所以，b2（c）也是c的递减函数。即在该模型中也依然是由能力最高的参赛者获得竞赛。但是，不同的是，由于众包方在开始时隐瞒了第2阶段竞赛的存在，故参赛者在第1阶段的努力不具备整体策略性。此时众包方的收益为

等式右边的第1部分等于Rnofd和RTknown，而第2部分显然大于0，故

②收益为最大努力。如果众包方的收益为所有参赛者中的最大努力水平，即获胜者的努力水平，则众包方的收益为

容易发现，中的第1组成项等于，故＞。再比较和，可以发现，的第1项大于的第1项，而的第2项却小于的第2项既可能大于也可能小于，关键取决于F（c）的形式和n、k的取值。

4 众包方的策略选择

将众包方选择3种不同反馈策略所能获得的收益（分努力总和及最大努力两种情况）总结如表1所示。

表1 不同反馈策略下参赛者和众包方的收益

4.1 收益为努力总和

由表1可知，当众包方的收益为总努力水平时，众包方采用无反馈策略和事先声明反馈策略所获得的收益相等，而事先隐瞒反馈策略优于上述两种策略。但是，值得注意的是，如果市场上都是有经验的参赛者，或者众包方和参赛者之间有重复交易关系，那么事先隐瞒反馈策略就不太容易见效。而当众包方出于某种原因（如为了保持良好的声誉）不能选择事先隐瞒反馈策略时，那么选择无反馈策略和选择事先声明的有反馈策略无差异。

对事先隐瞒反馈策略做深入分析后发现，如果众包方事先隐瞒了自己的反馈策略，那么参赛者在得到反馈后将面对一个囚徒困境：如果他们都不再追加努力，那么他们各自可获得的收益最大。但是，如果他们中间有一个人追加了努力，其他人都不变，那么这个人的收益变大，而其他人的收益变小。因此都不追加努力不是一个均衡解，相反，大家都会追加努力。当然在某些特殊的情况下，参赛者之间可能达成某种默契，均不追加努力。但是，在众包竞赛的环境下，参赛者的来源很广，彼此之间不相识且难以沟通，达成默契的可能性非常小，所以众包方采用事先隐瞒策略通常可以获得较大收益。

另一个值得注意的问题是反馈通常具有成本，如在第1阶段竞赛结束后，众包方要对所有参赛者的表现进行评估，然后才能选出表现靠前的若干位参赛者给予反馈，这就会产生评估成本，并且参赛者人数越多，评估成本越大。另外，撰写反馈意见，与参赛者就反馈意见进行沟通，都可能产生成本。无论是事先声明还是事先隐瞒的有反馈竞赛，它们的反馈成本是相同的，而无反馈竞赛则不存在反馈成本，因此，当反馈成本高于时，无反馈将成为最优策略。

4.2 收益为最大努力

当众包方的收益由所有参赛者中的最大努力水平，即获胜者的努力水平决定，那么众包方的反馈策略选择将和上述努力总和的策略选择有所不同。在前两节的分析中，已经指出且，即无论是事先声明反馈还是事先隐瞒反馈都比无反馈策略好。而和孰优孰劣则由参赛者的人数及能力分布和收到反馈的人数所决定。如果由于某些原因众包方无法选择事先隐瞒的策略时，众包方应该选择事先声明的有反馈策略。如果反馈成本高于时，无反馈将成为最优策略。

4.3 算例

首先，给出众包方的收益为所有竞赛者努力总和的算例。

假设存在n=6位参赛者，其能力参数分布为F（c）=2c—1（在［0.5，1］上均匀分布）。奖金总额为1。众包方将对k=2位表现最好的参赛者给予反馈。通过计算可知，如果众包方在竞赛中不提供反馈，则其收益=1.58；如果众包方事先声明在竞赛过程中会给予反馈，则其第1阶段收益R1=0.19，第2阶段收益R2=1.40，总收益为=1.59；反之，如果众包方事先隐瞒在竞赛过程中会给予反馈，则其第1阶段收益R1=1.58，第2阶段收益R2=0.11，总收益为=1.69。显然＞且，即事先隐瞒优于事先声明和无反馈策略，两者仅相差0.01，该误差可能由计算时的近似取值引起。另由和的值可知，如果反馈成本大于0.9，则众包方应选择无反馈策略。

接着，给出众包方的收益为所有竞赛者中最大努力的算例。仍然假设存在n=6位参赛者，其能力参数分布为F（c）=2c—1（在［0.5，1］上均匀分布），奖金总额为1。众包方将对k=2位表现最好的参赛者给予反馈。通过计算可知，如果众包方在竞赛中不提供反馈，则其收益=0.89；如果众包方事先声明在竞赛过程中会给予反馈，则其收益=1.13；反之，如果众包方事先隐瞒在竞赛过程中会给予反馈，则其收益=0.97。所以在该竞赛条件下，众包方事先声明的反馈策略是最优策略。当然，如果反馈成本大于—=0.24，众包方应选择无反馈策略。

5 结论

众包方在竞赛的过程中可以就参赛者的表现给予反馈以激励参赛者更加努力，但是并不是所有情况下给予反馈都是最优策略，有时不给予反馈反而可以带给众包方更多的收益。已有不少研究对竞赛中的反馈策略进行了比较，给出了不同策略占优的条件。然而，在这些研究中均存在一个前提，众包方在竞赛开始时就公布了自己的反馈策略，并且在竞赛过程中严格执行该策略。而在现实中，如果对众包方的行为没有约束，众包方就有可能不预先公布自己的反馈策略，或者预先公布一个虚假的策略，以牟取更大的收益。

在网络市场中，约束众包方投机行为最常见的措施是建立声誉机制。然而，在众包竞赛市场中，很多交易是单次的、非重复的，并且由于很难做到实名注册，故声誉机制也不尽完善，众包方有可能采取投机行为来获利，其中就包括采用事先隐瞒的反馈策略。因此，本文将事先隐瞒的反馈策略也纳入了研究范畴。

为了更好地理解众包竞赛中众包方的反馈策略选择问题，本文对无反馈、事先声明的反馈策略和事先隐瞒的反馈策略分别加以分析、比较，得到以下结论：众包方的策略选择与其收益类型有关。当众包方的收益由所有参赛者的努力总和决定时，无反馈策略和事先声明的有反馈策略为众包方带来相同收益，而事先隐瞒的有反馈策略带来的收益最大；当众包方的收益由所有参赛者中的最大努力水平决定时，无反馈策略带来的收益最小，事先声明和事先隐瞒的有反馈策略都有可能占优，最优策略由参赛者人数、能力分布以及反馈人数所决定。简言之，本文分析了在众包竞赛过程中众包方是否应该给予反馈，以及如何给予反馈，所得结论对于理解和设计有效的众包竞赛反馈机制皆有贡献。

附录

证明已知