修正KMV模型在创业板上市公司信用风险度量中的应用分析

杨开宇

摘   要：针对传统KMV模型在我国目前创业板的市场环境下不适用的状况，本文在继承现有研究成果的基础上，对模型加以进一步的修正，将通过市盈率推导出的预期增长率引入到KMV模型中，并采用EGARCH（1，1）模型对公司资产价值的波动率进行了预测。通过对13家创业板上市公司和13家中小企业板上市公司的信用风险进行评估检验，结果表明，利用修正后的KMV模型能够较好地识别出创业板上市公司和中小企业板上市公司之间信用风险的差别，比较准确地把握上市公司信用质量的变化趋势。

关键词：KMV模型;创业板;信用风险;EGARCH

中图分类号：F830.31                   文献标识码：B                      文章编号：1674-0017-2015（5）-0046-06

一、背景

创业板在国内是指专为暂时无法在主板上市的高科技和创意型中小企业提供融资途径的证券交易市场，创业板的推出为中小型企业提供了另一种英美式的证券融资方向。这对建立多层次资本市场体系，进一步缓解中小企业融资难的矛盾具有重要意义。所以说创业板是对主板市场的一种重要补充，其在资本市场的位置不容忽视。

信息不对称是中小企业中小公司难以借到长期贷款的重要原因，这同时也是创业板上市公司信用风险的主要诱因。但信息不对称是客观存在于市场经济中的。信息不对称而诱发的“机会主义”是市场中信用风险的主要原因。特别是国内，监管制度的漏洞，上市公司信息披露的不规范、制度不健全，导致上市公司信息披露作假等违规行为时有发生。著名的“银广夏”事件就让投资者损失惨重。而创业板公司以更低的条件上市，必然会带来更严重的信息不对称现象。创业板退市制度的出台使得一些上市公司的利润风险进一步加大，所以信用问题的揭露与评估对于有关监管机构及投资者都尤为重要。

目前，我国的信用风险管理水平也仅仅限于专家评估法等传统的度量方法，内部评级才处于起步阶段， 外部信用评级机构难以提供太多帮助。我国尚未能向发达国家一样拥有内外部评估角度多元、传统与现代多种评估方法结合的信用评估体系。所以找到一个较适合国内现状、评估相对较准确的信用评估方式具有重要意义。

二、现代信用风险管理模型综述与比较

当前，我国商业银行对信用风险的评价多选用定性分析方法（5C），作为贷款发放的重要依据，这种方法显得主观色彩浓厚。在国外，多元化的定量分析技术已经成为银行评估信用风险的重要依据。J·P摩根的Credit Metrics 模型、瑞士信贷银行的 Credit Risk + 模型、麦肯锡公司开发的 Credit Portfolio View 模型以及运用B-S公式的 KMV 模型等，都对信用风险度量提供了现代评估方法。 Logistic 模型是早期开发的传统信用风险量化模型，随着企业经营模式的转变和资本工具的衍生，其适用特征逐渐消失。Credit Metrics模型和 Credit Portfolio View 模型都是基于信用评级矩阵开发出来的计量模型，此方法的缺点在于假定同一信用等级企业违约率一样，将信用等级与信贷质量划等号。其在中国市场的应用更是具有致命的缺点，即国内尚未建立起较为成熟的征信系统，信用数据的缺乏难以支撑起Credit Metrics的良好应用。Credit Risk + 模型的构建需要历史违约数据，但考虑到我国依旧是以宏观调控为主的市场经济体制，且缺乏历史违约数据。因而，Credit Risk + 模型应用难度较大。

1974年，KMV模型作为一种违约预测模型，由KMV公司开发，以Merton提出的将Black-Scholes option pricing model应用于公司价值评估为基础。他通过上市公司资产预期的市场价值、波动率以及负债的账面价值来预测公司的信用风险。根据Merton理论，可以将公司的债权视为一个对公司资产的call option 。其假设公司仅有一种债务，call option 的执行价格为债务面值;到期期限为债务到期期限。当公司资产在债务到期时不足以抵付债务，则认定公司将违约，所有资产被转给债权人。否则公司将继续存在。这样，公司的股权价值可以通过option pricing 得到。

KMV衡量了风险的基数，相对于序数衡量，它更能反映出风险之间的具体差异，而不是简单的排序比较。KMV模型中的资产波动率来源于股价的计算，这在一定程度上反映了投资者对公司未来的预估。这种方法具有一定的前瞻性，从预测的运用看较优于别的依赖历史数据向后看的模型。KMV不依赖于会计报表的特性有效地弱化了国内会计数据夸大作假现象带来的分析偏误。此外，KMV模型所需求的股票数据不需要考虑市场的有效性，这对国内的弱势有效市场又是一种包容。21世纪以来，国内许多学者对KMV模型在国内的应用结果进行了验证。张玲和张佳林（2000）比较研究了KMV模型与其他模型，认为KMV模型比其他只看重财务数据的信用风险模型更适用于评价上市公司的信用风险。马若微（2006）首次将KMV模型运用到财务困境预警中，证明其在预警中国上市公司财务困境的可行性。翟东升、张娟和曹运发（2007）选取A股的ST公司和非ST公司各15家2005年的数据作为样本，检验了KMV模型的有效性，得出结论：KMV模型输出的违约距离（DD）有效地识别ST公司与非ST公司，并且随着公司被ST时间的临近，模型的识别能力越来越强。

综上，相比其他信用风险模型，KMV模型在应用于国内市场有极大的优势。所以本文选用KMV模型度量与分析创业板上市公司的信用风险，并验证KMV模型在创业板运用的可行性。

三、KMV原理

KMV模型以期权定价公式为基础。它认为一个公司（或企业）之所以违约是因为其资产的市场价值下降到负债的账面价值之下，丧失了偿债能力。模型提出了预期违约概率（Expected Default Frequency，EDF）这一概念，认为通过公司资产预期价值的概率分布可以计算出公司的预期违约概率，从而得出预期违约损失（Expected Default Loss）。

KMV模型的基础BSM 模型有一系列假设条件，包括：（1）交易无摩擦，无卖空限制。（2）存在无风险利率保持到期日前不变。（3）标的物价格服从GBM几何布朗运动。在此基础上Black和Scholes提出了期权定价公式。

GBM：dS=μSdt+σSdw

式中：S 为标的证券的价格;常数μ为drift（漂移率）及证券的瞬间期望收益;σ为证券价格的波动率;dw为标准维纳过程。

在上述假设的基础上，一份European call option的价值可以由下式给出：

E=VN（d1）-De N（d2）                                   （1）

当d = ，d2=d1-σ

式中： Δt 为距到期日时间;D为企业债务，作为strike price（执行价）;N（d）为标准正态分布，σ 为企业市场价值的波动率， E为企业股票市值，V为企业资产价值。

对公式1式两边进行求微分并简化得到：

dE=N（d1）dv                                                （2）

即：σ =N（d1） σ                                          （3）

关于资产价值波动率与股权价值波动率的关系函数，鲁炜（2003）运用了中科大信用研究结果：

=   t e dt。

本文依旧采用传统的关系函数。然后通过联立公式 1和公式 3 就可以得出V 和σ 。根据公司中短期负债和长期负债和长期负债来确定违约点DPT，再通过公式：DD= 计算出公司的违约距离，由于KMV公司的违约距离和EDF的一一映射关系是建立在美国公司的数据上，这未必适用于中国的公司，且中国目前缺乏全面的违约数据，所以我们难以确定公司的EDF，但用违约距离来衡量公司的信用状况依旧是可行的。

四、样本选取与参数设定

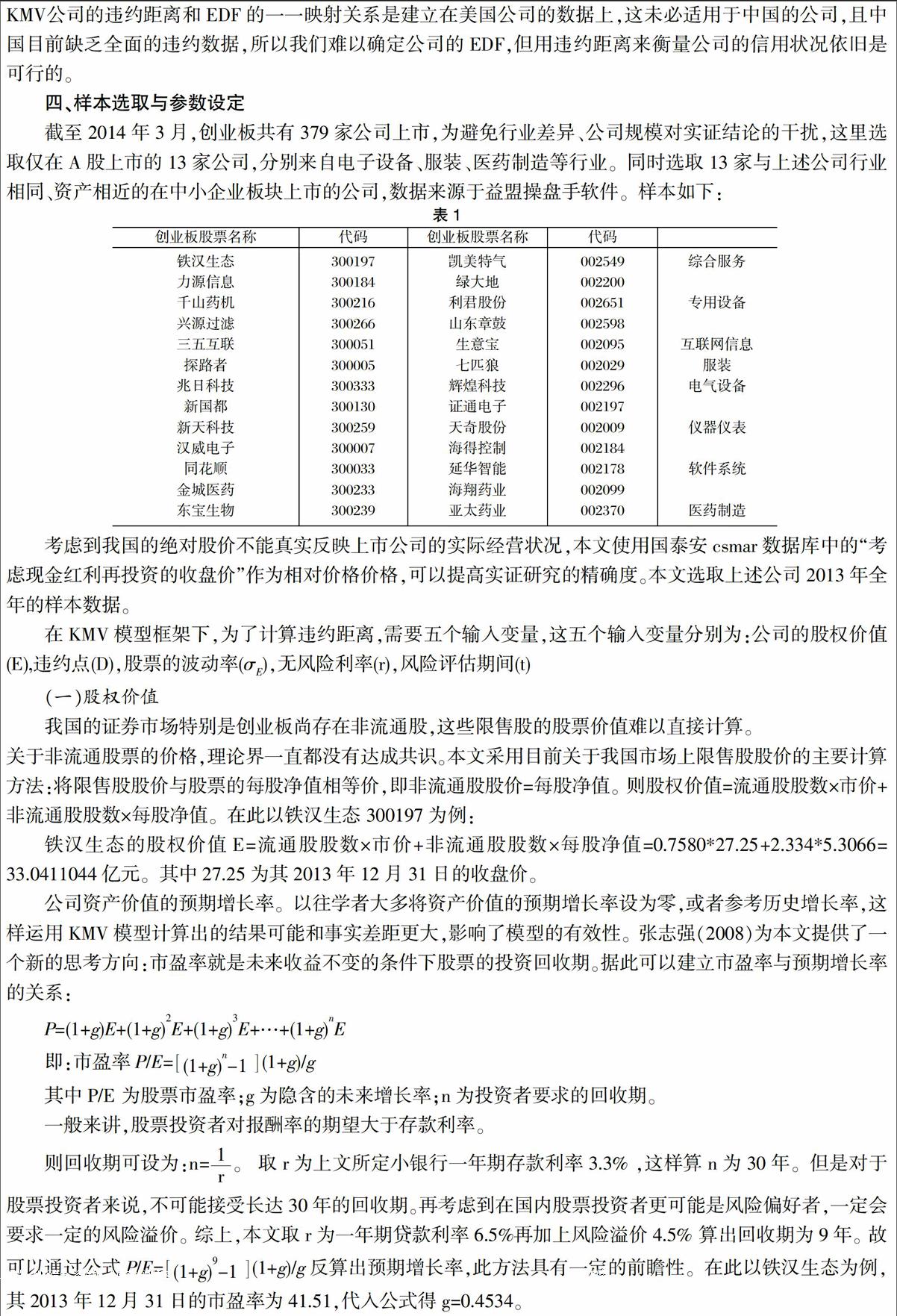
截至2014年3月，创业板共有379家公司上市，为避免行业差异、公司规模对实证结论的干扰，这里选取仅在A股上市的13家公司，分别来自电子设备、服装、医药制造等行业。同时选取13家与上述公司行业相同、资产相近的在中小企业板块上市的公司，数据来源于益盟操盘手软件。样本如下：

考虑到我国的绝对股价不能真实反映上市公司的实际经营状况，本文使用国泰安csmar数据库中的“考虑现金红利再投资的收盘价”作为相对价格价格，可以提高实证研究的精确度。本文选取上述公司2013年全年的样本数据。

在KMV模型框架下，为了计算违约距离，需要五个输入变量，这五个输入变量分别为：公司的股权价值（E），违约点（D），股票的波动率（σ ），无风险利率（r），风险评估期间（t）

（一）股权价值

我国的证券市场特别是创业板尚存在非流通股，这些限售股的股票价值难以直接计算。

关于非流通股票的价格，理论界一直都没有达成共识。本文采用目前关于我国市场上限售股股价的主要计算方法：将限售股股价与股票的每股净值相等价，即非流通股股价=每股净值。则股权价值=流通股股数×市价+非流通股股数×每股净值。在此以铁汉生态300197为例：

铁汉生态的股权价值E=流通股股数×市价+非流通股股数×每股净值=0.7580*27.25+2.334*5.3066=33.0411044亿元。其中27.25为其2013年12月31日的收盘价。

公司资产价值的预期增长率。以往学者大多将资产价值的预期增长率设为零，或者参考历史增长率，这样运用KMV模型计算出的结果可能和事实差距更大，影响了模型的有效性。张志强（2008）为本文提供了一个新的思考方向：市盈率就是未来收益不变的条件下股票的投资回收期。据此可以建立市盈率与预期增长率的关系：

P=（1+g）E+（1+g） E+（1+g） E+…+（1+g） E

即：市盈率P/E=（1+g） -1（1+g）/g

其中P/E 为股票市盈率;g为隐含的未来增长率;n为投资者要求的回收期。

一般来讲，股票投资者对报酬率的期望大于存款利率。

则回收期可设为：n= 。 取r为上文所定小银行一年期存款利率3.3% ，这样算n为30年。但是对于股票投资者来说，不可能接受长达30年的回收期。再考虑到在国内股票投资者更可能是风险偏好者，一定会要求一定的风险溢价。综上，本文取r为一年期贷款利率6.5%再加上风险溢价4.5% 算出回收期为9年。故可以通过公式P/E=（1+g） -1（1+g）/g反算出预期增长率，此方法具有一定的前瞻性。在此以铁汉生态为例，其2013年12月31日的市盈率为41.51，代入公式得g=0.4534。

（二）违约点

KMV公司在确定违约点DP的时候，对规模、行业、时期各不同的上巿公司进行了大量实证研究。测试的结果表明，当把上市公司的流动负债加上非流动负债的一半作为违约点时，KMV模型预测上市公司信用风险最有效。本文采取KMV公司定义的违约点，即DPT=STD+50%LTD。

（三）无风险利率与期限

本文选择银行一年期定期存款利率。以2013年1月的一年定期存款利率为例，大银行如工商银行、农业银行的利率为3.25%;小银行如华夏银行的利率普遍为3.30%

虽然银行规模的扩大并不必然导致中小企业的融资困境。但相比小银行，大银行的重心并不在中小企业贷款上，所以小银行的关系型贷款适用于绝大部分中小企业。依此，本文选取小银行的一年期定期存款利率3.30%，设定违约距离的计算时间为一年，即Δt=l。

（四）股价波动率

之前文献大量使用GARCH（1，1）对于股权价值波动率进行估计，但是对称模型GARCH是假设标的物收益率服从正态分布的，这与现实状况中创业板收益率分布不符。而且GARCH模型忽略了现实中波动率变动的非对称性。据此，本文采用非线性模型EGARCH，在计算每个交易日股权收益率r =1n 后，使用Eviews5.0对股权价值波动率进行建模，得出σE。

本文将采用样本中各公司2013年一年的日对数收益率来对EGARCH（1，1）模型进行拟合。其中日对数收益率的计算如下：u =1n（s /s ）

其中s 、s 分别为第i日和第i-1日股票收盘价。

由于篇幅有限，本文以铁汉生态（300197）为例，利用Eviews5.0的EGARCH工具计算公司股权价值的波动率σv。

（1）计算日对数收益率并对收益序列进行统计分析，对Jarque-Bera统计图（图1）进行分析可知：

首先，收益率的kurtosis值为5.98，大于3，说明该股票的收益率分布存在明显的“尖峰厚尾”特征;其次，skewness=0.567，与0有明显的差别，呈现左偏特征。该股票的收益率的JB统计量为100左右，所以可以在99%上拒绝其收益分布正态的假设，并认定其收益分布呈现“厚尾”特征。表明利用EGARCH模型来对波动率进行拟合具有一定的合理性。

（2）平稳性检验

本文在这里采用ADF单位根检验法。从表1可以看出，统计量的绝对值13.94远大于1%或5%标准下临界值的绝对值3.46和2.87，因此可以判定收益率时间序列在1%标准下是显著平稳的，说明利用EGARCH（1，1）模型进行检验是有效的。

（3）相关性检验

运用自相关函数ACF及Ljung- Box- PierceQ对收益序列的检验结果如表2。滞后阶数为 15。序列的ACF和PACF值在大部分时滞上都较小，表明序列无自相关性，无需引入自相关性的描述部分。这一点也得到了Q检验的验证。

（4）建立波动性模型

由于铁汉生态收益率序列为平稳序列，且存在较弱的自相关，所以建立如下日收益率方程：r =r +ε

对收益率的residual ε 进行ARCH检验，检验其是否具有ARCH效应，收益序列的ARCH滞后1阶的检验结果如表3。可以发现，ARCH检验的LM统计量Obs*R-squared的p-value为0.02左右，故在5%显著水平下拒绝原假设，残差序列存在ARCH效应，适宜采用EGARCH模型。

（5）EGARCH模型的参数估计与检验

我们通过EGARCH模型考察信息冲击曲线的对称性：建立EGARCH（1，1）模型，

1n（σ  ）α +α  +r +λ1n

通过Eviews的EGARCH计算，结果形式为：

1n（σ  ）=-0.044+0.0684 -0.0645 +0.981n

可以看出 的系数C（3）明显在统计意义上显著，说明EGARCH模型比GARCH模型在同等条件下更好的捕捉到了收益率非对称的特征。

此外对EGARCH模型的残差值进行Ljung Box-Q 检验，如图2。发现与原模型相比，Q-Stat值均缩小许多，故可以认为EGARCH模型消除了ARCH效应通过检验。

至此，可以建立EGARCH（1，1）模型：

1n（σ  ）=-0.044+0.0684 -0.0645 +0.92n

计算出铁汉生态的年化股价波动率为0.396707275。通过类似办法，可得出所有公司的年化收益率。

五、实证及检验

在已知公司股权价值E、股权价值波动率σE、违约点、市场利率r、Δt以及市盈率P/E，通过Matlab求解非线性方程，可以得到计算违约距离所需的V、σv和g。再通过公式DD= 即可算出公司的违约距离，如表4。

通过图3可以看出在各个行业内比较，创业板公司的DD明显比中小企业板块公司要低。

本文对来自创业板与中小企业板这两个配对样本数据分别进行了t检验与wilcoxon检验，通过分析两配对样本，对样本来自的两总体的分布是否存在差异进行推断。stata分析结果如表5与表6。

由表5、6可知，t-test统计量为3.1436，对应的概率p值为0.0042，小于5%显著性水平。wilcoxon检验中负号秩总和为9，正号秩总和为82，两者存在较大差异，z-test统计量为2.551，对应的概率p值为0.0107，小于5%显著性水平。综上可以拒绝原假设，即认为创业板上市公司与中小企业板公司在违约距离上存在显著差异。

如上表数据所示，创业板公司的平均违约距离约为2.207，明显小于中小板公司的2.483;再看创业板公司的平均资产波动率为0.43，比中小板企业多0.08这在一定程度上解释了违约距离的差异。直观上理解，相比中小板企业，创业板企业存在规模小，业绩不稳定，技术不成熟以及信用问题，所以创业板公司的总体信用水平要低于中小板企业，本文样本中存在部分创业板企业违约距离大于配对中小板企业的现象，而且样本之间的均值差仅为0.277，这可能与2012年创业板退市制度实行，加强了对创业板公司的风险监管有关。

若想要降低创业板公司的违约率，需要改善公司的资本结构，多元融资，同时通过制度的完善以及创业者教育等方法，平抑创业板的资产价值波动率，这样才能使得创业板企业有更好的发展。

六、KMV应用建议

随着创业板公司上市门槛逐渐降低，应该加快关于创业板上市公司法律的支撑，加大监管力度。

建立我国自己的违约数据库。KMV公司的数据库是建立在美国上巿公司基础上的，并不适用于国内。未来几年创业板上市公司会大幅增多，但对于投资者来说，其投资风险也也不可忽视。所以建立公司的违约数据库、给投资者重要的信用风险参考，对未来我国创业板市场的发展具有重要的意义。

加强信用风险管理人才培养。专业人才的短缺一直是我国应用国际先进信用风险评估方法的一大障碍。为提高我国证券市场信用风险管理水平，应加强高素质风险人才的培养。

参考文献

[1]Creditmetrics TM-Technical Document， J.P. Morgan & Co. New York，April 1997.

[2]CreditPortfolio View TM approach documentation and user's documentation， McKinsey and Company， Zurich， 1998.

[3]Hull，J.C. （2005） Options， futures and other derivatives， 6th edition， Person Prentice Hall.

[4]Peter J. Crosbie， Jeffrey R. Bohn. Modeling Default Risk[R]. SAN FRANCISCO. KMV. LLC， 2000.

[5]陈敏，冯伟，彭志云.基于KMV模型的商业银行房地产贷款信用风险研究[J].湖南财政经济学院学报，2012，（6）：74-78。

[6]梁笛.银行资产规模与中小企业信贷—大银行和小银行比较优势研究[J].东南亚研究，2007，（3）：87-91。

[7]林林，徐翔宇.信用风险模型综述及对我国借鉴[J].金融经济，2009，（2）：58-59。

[8]马若微.KMV模型运用于中国上市公司财务困境预警的实证检验[J].数理统计与管理，2006，（5）：593-601。

[9]马宁.商业银行信用风险管理研究[D].江苏：东南大学，2004。

[10]潘淑婷.基于修正KMV模型的创业板公司信用风险研究[J].中国证券期货，2010，（9）：36-37。

[11]张志强.市盈率与增长率关系的探讨—兼论股票定价的有关问题[J].财经问题研究，2008，（1）：67-72。

[12]张玲，杨贞柿，陈收.KMV模型在上市公司信用风险评价中的应用研究[J].系统工程，2004，（11）：84-89。

[13]翟东升，张娟，曹运发.KMV模型在上市公司信用风险管理中的应用[J].工业技术经济，2007，（1）：126-127。

[14]周杰.修正的KMV模型在上市公司信用风险度量中的应用分析[J].财会通讯，2009，（15）：8-10。

The Analysis on the Application of the Modified KMV Model in the Measurement of the Credit Risk of Listed Companies in the Second-board Market

YANG Kaiyu

（Risk Control Department， China UnionPay，Shanghai，200135）

Abstract：Aimed at the situation that the traditional KMV model is not applicable to the environment of the second-board market at present in China， based on inheriting the existing research results， the paper further modifies the model， introduces the expected growth rate deduced by the earnings multiple ratio to KMV model， and uses EGARCH （1， 1） model to predict the volatility rate of the asset value of the company. Based on evaluating the credit risks of 13 listed companies in the second-board market and 13 listed companies in small and medium-sized enterprise board market， the results show that using the adjusted KMV model can well identify the difference of the credit risk between 13 listed companies in the second-board market and 13 listed companies in small and medium-sized enterprise board market， and more accurately grasp the change trend of the credit quality of listed companies.

Keywords： KMV model; second- board market; credit risk; EGARCH

责任编辑、校对：张宏亮