水平受荷桩的变形性能与承载力的灰色系统法预测

赵会永，张玉洁，钟 涛，张东辉

（北方工程设计研究院有限公司 ，河北石家庄050000）

水平受荷桩的变形性能与承载力的灰色系统法预测

赵会永，张玉洁，钟 涛，张东辉

（北方工程设计研究院有限公司 ，河北石家庄050000）

摘要:水平受荷桩-土相互作用体系的复杂性决定了该系统很多信息是未知的，试图完全弄清楚桩-土共同作用体系的力学机理并建立准确的力学模型，进而建立完全准确的数字模型进行精确分析几乎是不可能的，这正符合灰色系统的特点。应用灰色系统理论对某项目湿陷性黄土地基中的水平受荷桩建立了相应的数学模型，并与桩水平荷载试验数据进行了对比，满足工程精度，能较好的适用于同类工程。采用灰色系统法预测桩的变形曲线与承载力可在工程实践中进行应用和进一步发展，当积累足够多的试验与预测数据后，可直接通过预测模型绘制同类工程条件下同一桩型的桩变形曲线，进而判断桩的水平承载力，缩短工程工期并降低工程投资。

关键词:水平受荷桩；桩土共同作用；灰色系统；变形曲线与承载力

1　工程地质条件［1］

本项目场区地貌单元为黄土塬，位于甘肃省庆阳市西峰区董志镇，地形平坦，起伏不大。

拟建场地属半干旱内陆性季风气候区。钻孔最大揭示深度40 m，地下水埋深一般为29.5 m～33.5 m左右。地层共13层，①层粉质粘土为黑垆土Q4；②层～④层粉质粘土为马兰黄土Q3；⑤层～层粉质粘土为离石黄土上段Q2。勘探场区，湿陷性黄土的湿陷程度由上向下逐渐减弱，一直渐变为非湿陷性黄土。②层～⑤层粉质粘土为湿陷性黄土，底界埋深16 m左右。由此可见Q3的马兰黄土和Q2顶部的离石黄土为湿陷性黄土。场地黄土的湿陷等级为Ⅱ级，湿陷类型为自重湿陷性黄土场地［1］。

2　关系曲线的预测方法

2.1GM（1，1）预测模型［1-3］

基于灰色理论建立水平受荷桩 H-y0关系曲线的GM（1，1）模型时，将水平位移y0看做广义时间建立了荷载序列的GM（1，1）模型，其灰微分方程为:

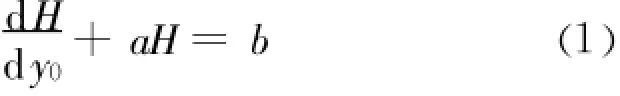
其中:H为预测灰数，本研究中的桩顶水平荷载序列；y0为桩顶水平位移量序列 ；a为发展系数（1/mm）；b为灰作用量（kN/mm）。

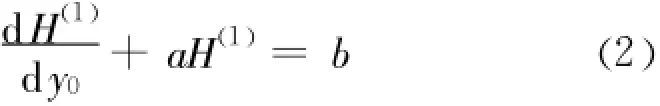
其中:

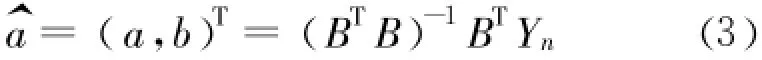
其中:

由式（3）、式（4）、式（5）求得 a，b然后代入式（2）并求解该微分方程可得:

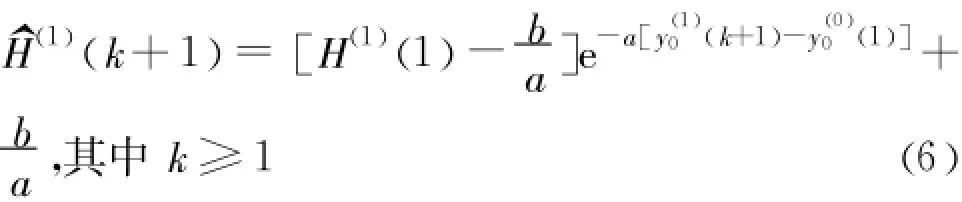
或者

式（6）、式（7）可分别对桩顶水平荷载及桩顶水平位移进行预测。若已知桩顶的水平荷载，则桩顶的水平位移量的预测值可由式（7）求出。在大部分情况下，式中的 a值是特别小的正数。式（6）取极限可得:

因为单桩的水平极限承载力为

2.2水平受荷桩GM（1，1）预测模型的检验

首先建立荷载的残差序列

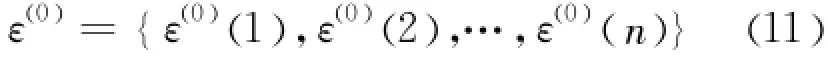
其中

（1）残差检验［3］

预测的精度可通过式（13）、式（14）看出。

（2）后验差检验

后验差的检验标准见表1［1-3］。

表1　预测精度等级

（3）小误差概率合格模型检验

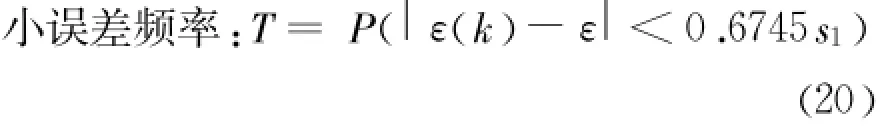
对于给定的 T0，小误差概率 T＞T0时，称模型为小误差概率合格模型。通常，T＞0.95为优；T＞0.80为合格；T＞0.70为勉强合格；T≤0.70为不合格［4］。

（4）灰关联度检验

设参考序列为 H（1），比较序列为 ＾H（1），则其灰关联系数为［6-10］:

则其灰关联度为:

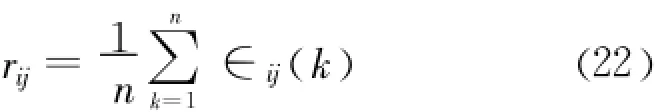
关联度的检验标准见表2［5］。

表2　预测精度检验表

当预测值的关联度检验结果不满足其检验标准要求时，需建立残差GM（1，1）模型，进行残差修正。

2.3水平受荷桩残差GM（1，1）修正

残差序 列ε（0）=｛ε（0）（1），ε（0）（2），…，ε（0）（n）｝，必须满足 n≥4且ε（0）恒为正值或者负值。对该序列进行一次累加运算可得 ε（1）= ｛ε（1）（1），ε（1）（2），…，ε（1）（k0）｝然后建立残差的GM（1，1）模型［6-10］:

其中:

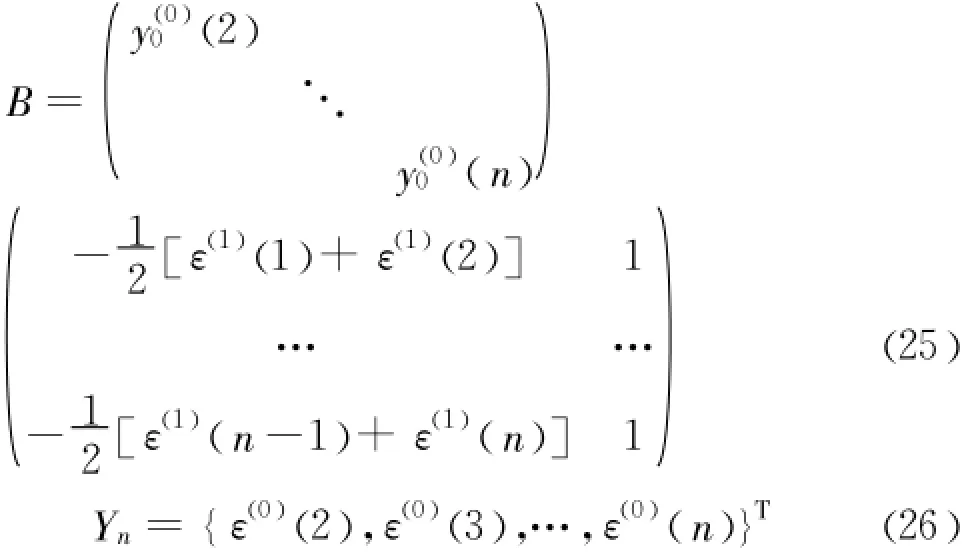
进而可得到ε（1）的广义时间（水平位移）响应序列式为:

对进行一次累减运算（1-IAGO运算）就可得到残差ε（0）的模拟序列式为 :

原模型的模型修正可利用 ε（0），式（28）与残差序列的正负号取值一致。

3　工程实例实测与预测的对比分析

3.1建立桩的GM（1，1）模型

水平受荷桩S7为机械洛阳铲成孔灌注桩，桩长28 m，直径800 mm。试桩采用强度等级为C30的钢筋混凝土，水平极限承载力实测结果为 Hu=300 kPa（见表3）。

表3　S7试桩静载试验结果

荷载增量序列与水平位移增量序列可通过对表3中的数据进行处理后得到:

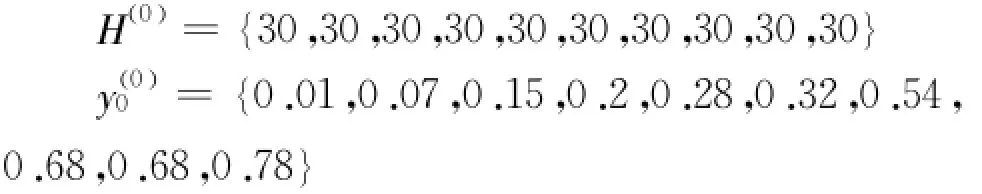
水平荷载序列与水平位移序列可经过1-AGO运算得到:

很明显这两个序列就是实测的水平荷载与水平位移。

将 H（0）代入式（5）可得 :

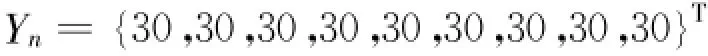
将矩阵 B与Yn代入式（3）可得:

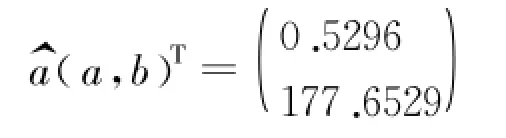
该桩采用灰色系统法预测的极限水平承载力可据公式（10）求得，二者的比值为300/335.45=0.8943，显然桩的极限水平承载力实测值与预测值较为接近，且预测值较大。这主要是因为试桩采用工程桩，试验时整个桩土作用体系未达到塑性极限破坏状态。而当桩进入塑性段时采用GM（1，1）预测模型有较好的精度。倘若静载试验时将试桩加载至破坏，实测值会更加接近预测值。

式（6）、式（7）代入所求 a，b求解后可得:

或者

预测的水平荷载序列＾H（1）与位移序列＾y（1）0可由式（29）与式（30）得到，见表4。

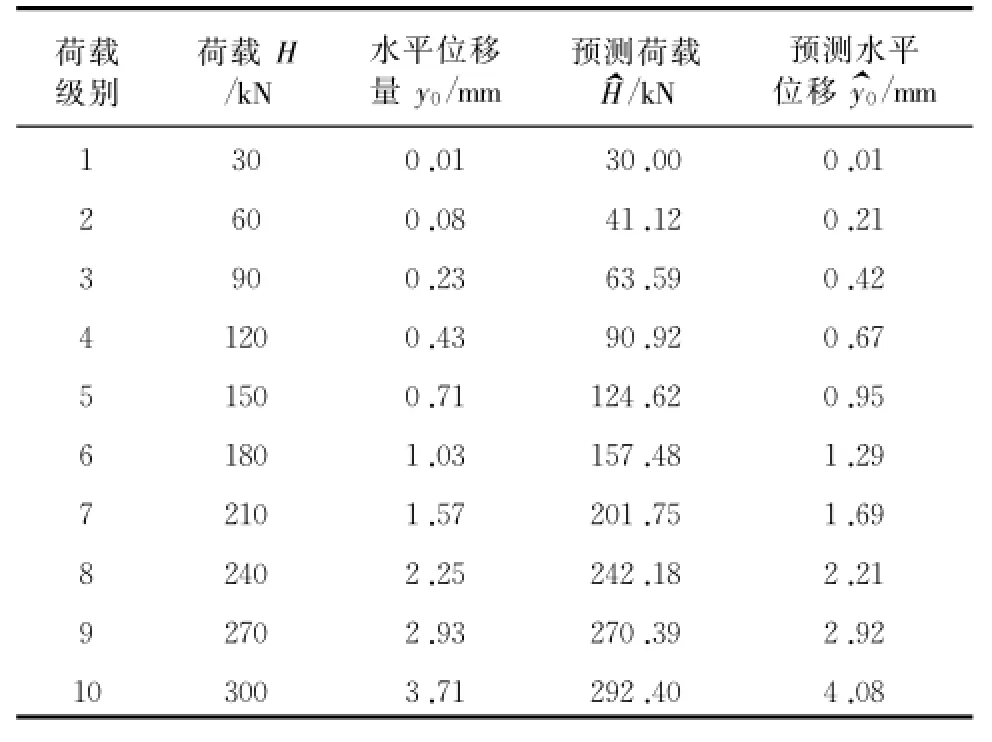
表4　S7桩水平静载试验实测值与预测值

预测所得的 H—y0曲线，如图1所示，可根据原始荷载与预测水平位移序列或实测位移与预测荷载序列绘制，两种方法所绘制预测曲线实质是一条曲线如图2所示。

实测曲线与预测曲线的存在一定差异，如图1所示。该模型的精度可由数字特征来反映。

3.2精度检验

由2.2中对水平受荷桩GM（1，1）的精度检验的方法，首先建立荷载序列的残差序列:

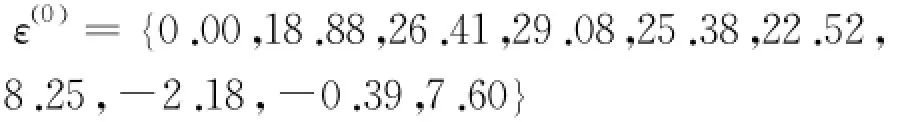
（1）残差检验

相对误差序列:

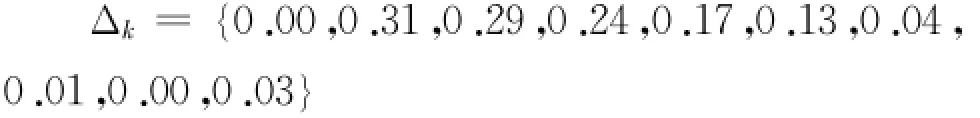
显然该模型预测的精度有待提高，因此必须建立残差模型对原预测模型进行修正。

（2）后验差检验

荷载序列的方差:

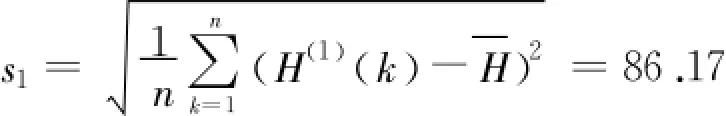
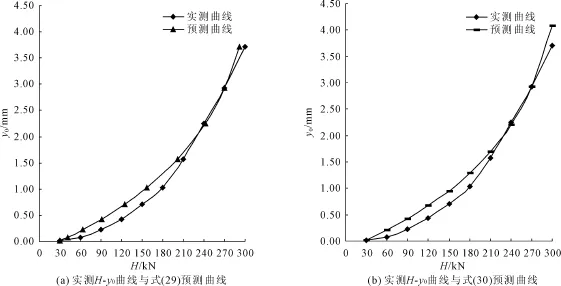
图1　实测 H-y0曲线与预测的 H-y0曲线对比

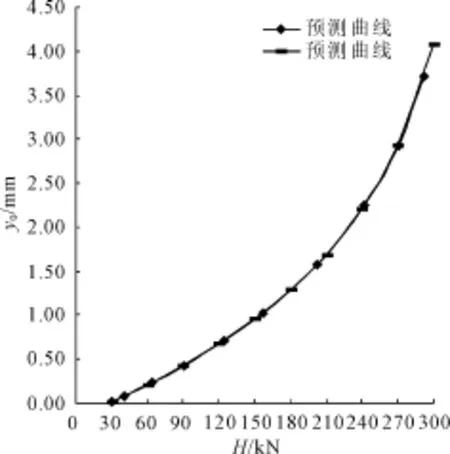
图2　不同公式得到的预测曲线对比

残差序列的方差:

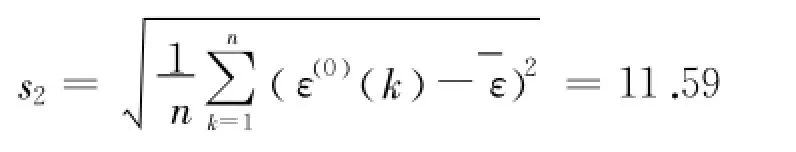
（3）小误差概率模型检验

小误差概率:

显然满足表1的要求。

（4）灰关联度检验

假设参考序列为H（1），比较序列为＾H（1），可求得灰关联系数:

则其灰关联度为:

据表2知，该模型灰关联度指标基本合格。因此须建立残差GM（1，1）模型，进行残差修正。

3.3残差GM（1，1）修正与精度再检验

可修正的残差序列根据2.3中提出的修正方法求得:

将矩阵 B和Yn代入式（24）可得:

将 aε，bε代入公式（28）可得残差ε（0）的模拟序列满足:

由式（32）所得的预测结果见表5。

表5　S7桩水平荷载静载试验实测值与预测值

由此可得残差修正后的 H—y0曲线见图3。

图3　实测 H—y0曲线与残差修正后预测的 H—y0曲线对比

显然，直观上经过残差修正明显提高了预测模型的精度。精度计算指标如下:

（1）残差检验

相对误差序列:

平均相对误差:

显然残差修正明显改善了该模型的预测的精度，且达到了精度要求。

（2）后验差检验

荷载序列的方差:

残差序列的方差:

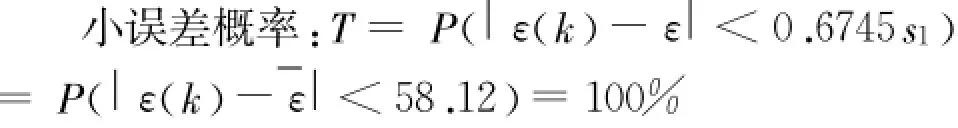
由后验差检验标准表1可知，后验差满足要求。

（3）灰关联度检验

在此预测模型的灰关联度的检验中 ，假设参考序列为荷载序列 H（1），比较序列为 ＾H（1）则其灰关联系数为:

则其灰关联度为:

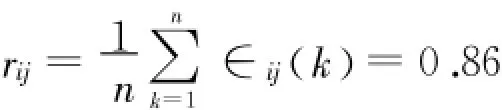
由表2可知不需要再进行残差修正，精度好。

3.4桩水平临界荷载的预测

将修正后的水平受荷桩的 H—y0曲线，进行坐标变化，转化为曲线，就可以根据确定临界荷载的方法曲线的第一直线段的终点所对应的荷载为水平临界荷载）预测该桩的水平临界荷载（见表6）。

由图5可知预测所得水平受荷桩的临界荷载为175 kN。由图4得到的水平受荷桩实测临界荷载为150 kN。实测结果与预测结果的相对误差为16.7%。

表6　S7桩水平静载试验预测值与位移梯度值

图4　实测荷载与其位移梯度曲线

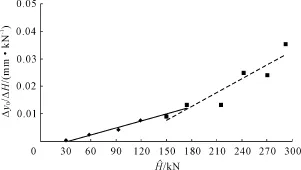
图5　预测荷载与位移梯度曲线

产生较大相对误差的原因，主要有两个:一是虽然灰关联度 rij=0.86，由表2可知其灰关联度很高，达到了“好”的标准，但是由于位移梯度对该误差比较敏感，就导致各段斜率的对该误差的反应较大，其临界荷载的预测精度只能达到83.3%。二是由于试桩为工程桩，桩水平静载试验时桩土共同作用体系未达到塑性破坏段，这就造成试桩的实测曲线与预测曲线的指数形式有一定差距，并且曲率较大，这就造成了实测水平临界荷载比预测的水平临界荷载较小。

4　结 论

（1）运用灰色系统理论对桩的水平荷试验中的试验数据建立GM（1，1）模型，由于模型存在一定误差，经过残差修正后得到了精度较高的水平荷载的广义时间（水平位移）的影响序列，能满足一般工程的需要。将最终水平荷载的广义时间（水平位移）的影响序列进行坐标变换后得到曲线，进而利用曲线预测了水平受荷桩的临界荷载，虽然仍具有一定的误差，但是其分析精度明显改善。

（2）采用灰色系统法预测桩的变形曲线与承载力可在工程实践中进行应用和进一步发展，当积累足够多的试验与预测数据后，可直接通过预测模型绘制同类工程条件下同一桩型的桩变形曲线，进而判断桩的水平承载力，进而加快工程工期并降低工程投资。

参考文献:

［1］ 赵会永，韩晓雷，水伟厚，等.灰色系统法预测分析抗拔桩单桩变形性能与极限承载力［J］.水利与建筑工程学报 ，2009，7（2）:17-19.

［2］ 胡卫东，甘 勇.粉喷桩单桩极限承载力预测［J］.岩土工程界，11（3）:65-67.

［3］ 唐军峰，胡详昭，汤新福，等.基于灰色系统理论的桩基承载力预测［J］.工程建设与设计，2004，（10）:41-44.

［4］ 罗战友，董清华，龚晓楠.未达到破坏时的单桩极限承载力预测［J］.岩土力学，2004，25（2）:304-307.

［5］ 姚怡文，赵扶民.灰色系统在预测单桩极限承载力的应用［J］.南昌大学学报:工科版，2004，26（2）:73-76.

中图分类号:TU473.1+1

文献标识码:A

文章编号:1672—1144（2015）01—0114—07

DOI:10.3969/j.issn.1672-1144.2015.01.024

收稿日期 :2014-11-04修稿日期:2014-12-06

作者简介 :赵会永（1982—），男，河北新乐人，硕士 ，工程师 ，主要从事地基处理、边坡与基坑支护、地基检测等方面的工作。E-mail:zhymylove@qq.com

The Prediction of the Deformation Behaviour and Bearing Capacity of Laterally Loaded Piles Using Gray System Theory

ZHAO Hui-yong，ZHANG Yu-jie，ZHONG Tao，ZHANG Dong-hui
（NORENDAR International Ltd.，Shijiazhuang，Hebei 050000，China）

Abstract:The complexity of the pile-soil interaction system determines that a lot of information of the system is unknown.It is almost impossible to fully understand the mechanics mechanism of pile-soil interaction system and to establish an accurate mechanical model，and then a completely accurate digital model for precise analysis.But these characteristics fit in the gray system very well.With the application of grey system theory for a certain project，the corresponding mathematical model of the laterally loaded pile in the collapsible loess was established.Compared with the measured value of the laterally loaded pile test，it was proved that the proposed model established by this method met the requirements of engineering accuracy.With the gray system method to predict the deformation and bearing capacity of the laterally loaded pile，the number of the test piles can be reduced under the similar engineering geological conditions.It has some significance for reducing the project cost and speeding up the construction rate.

Keywords:the laterally loaded pile；the pile-soil interaction system；gray system；deformation and bearing capacity