预应力型钢超高强混凝土梁抗弯性能有限元分析

孟 笑，贾金青，王耀波，王东来

（大连理工大学建设工程学部，辽宁大连116024）

预应力型钢超高强混凝土梁抗弯性能有限元分析

孟 笑，贾金青，王耀波，王东来

（大连理工大学建设工程学部，辽宁大连116024）

摘要:为进一步研究预应力型钢超高强混凝土梁的抗弯性能，利用ABAQUS对预应力型钢超高强混凝土梁进行数值分析。模型计算所得荷载-位移曲线与试验结果基本吻合，验证了有限元模型的正确性。结果表明 ，增加纵向受拉钢筋配筋率对混凝土开裂几乎没有影响 ，但使梁的屈服荷载和极限荷载均增加；型钢向下偏移 ，梁的屈服荷载和极限荷载增加；型钢向上偏移虽不能提高构件的承载力，但能改善梁的延性。增加预应力筋配筋率能延缓构件的开裂。

关键词:预应力；型钢；超高强混凝土；ABAQUS；抗弯性能

预应力型钢混凝土梁是一种新型的组合结构形式［1］，具有承载力高、刚度大、抗裂性能好的特点。将超高强混凝土应用到预应力型钢混凝土梁中，形成的预应力型钢超高强混凝土梁更能够充分发挥超高强混凝土材料、型钢和预应力结构的优点［2］。超高强混凝土具有抗压强度高，刚度大及耐久性好等特点；型钢可以提高梁的承载力，改善梁的延性；施加预应力能有效控制梁正常使用阶段的变形和裂缝的开展。预应力型钢超高强混凝土梁是一种新型的结构形式，目前国内外尚没有比较成熟的计算理论［3］，试验需耗费大量的时间和原材料，文献［4］采用ANSYS有限元程序开展了这种新型组合梁的数值计算分析，但其所得的荷载-位移数值计算曲线未体现出试件的峰值荷载后的受力阶段。为全面了解这种新型组合梁受力性能，本文利用有限元数值分析软件ABAQUS，开展了组合梁的全曲线数值计算分析。通过数值计算结果与试验结果的对比分析，验证了模型的正确性，并分析了纵向受拉钢筋配筋率、型钢含钢率、型钢位置及预应力筋配筋率对试件承载力的影响。

1　建立ABAQUS有限元计算模型

1.1模型尺寸及材料力学参数取值

对9根预应力型钢超高强混凝土梁和1根预应力超高强混凝土梁进行模拟。梁截面尺寸为200 mm×300 mm，全长为4 000 mm，跨度为3 700 mm。混凝土采用C100级超高强混凝土，保护层厚度为25 mm。纵向钢筋采用HRB335级钢筋，预应力筋采用1860级高效低松弛钢绞线，张拉控制应力为0.75 fpdk，预应力锚具采用低回缩锚具。型钢采用Q235级工字钢，箍筋采用HPB235级钢筋，支座处φ8@50，剪跨段内φ8@150，纯弯段内φ8@200。梁配筋见图1，截面形式见图2，各试件钢筋设计参数见表1，有限元模型各材料参数取值见表2。

图1　梁的配筋图

图2　梁的截面示意图

本文中数值计算的试件PSRCB-01，PSRCB-02，PSRCB-03及PSRCB-07与参考文献［3］中试验试件B-01，B-02，B-03及B-07截面配筋参数完全相同，用以验证数值模型的正确性。

表1　梁的设计参数

表2　钢绞线、钢筋及型钢的力学参数

1.2材料本构关系的选择

超高强混凝土的力学性能与普通混凝土有很大差别，表现为高脆性。从试验破坏特征上看，超高强混凝土呈突然的劈裂破坏 ，破坏前表面基本无裂缝，仅在破坏前瞬间内部会有劈裂声，之后突然炸裂，破坏面穿透石子、表面光滑［5-7］。超高强混凝土的应力-应变曲线的上升段呈直线［8-9］，而且强度越高线性越显著，下降段越陡，甚至可以认为没有下降段［9］。

《混凝土结构设计规范》［10］（GB50010-2010）中给定的混凝土本构模型仅适用于C80以下的混凝土，参考近年来土木工程研究人员的研究成果 ，本模型采用余志武、丁发兴［11-12］提出的超高强混凝土受压及受拉本构模型。超高强混凝土受压应力-应变全曲线表达式为:

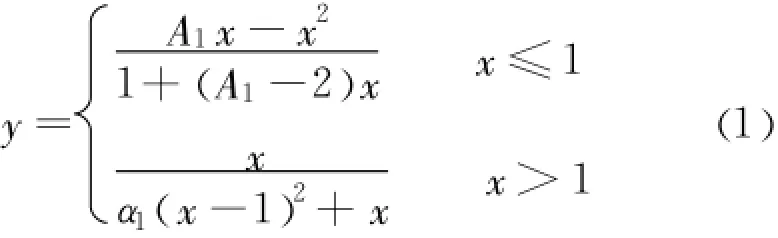
超高强混凝土轴心受拉应力 -应变全曲线表达式为:

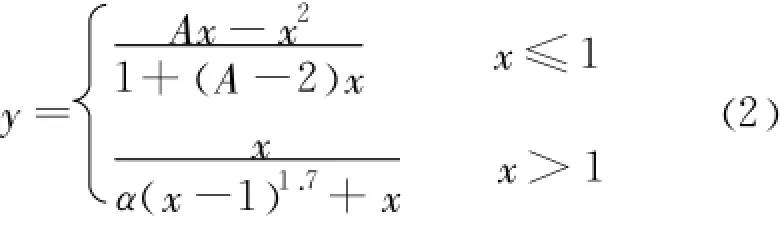
模型中的纵向钢筋、预应力筋、型钢及箍筋均采用双线性理想弹塑性模型进行模拟。

1.3预应力的施加方法

在使用ABAQUS建模时，常用的预应力施加方法有:降温法和Initial condition法。本文采用降温法进行数值建模。预应力施加方法为:在材料属性模块中对预应力筋定义膨胀系数，再在载荷模块创建温度预定义场，降低预应力筋的温度，从而实现预应力的施加。预应力筋的温度降低值计算公式为:

式中:F为预应力筋上施加的预应力的大小；α为预应力筋的温度线性膨胀系数，通常取值为1×10-5；E为预应力筋的弹性模量；A为预应力筋的截面面积。

1.4模型的建立

本模型采用分离方式建模，混凝土采用八结点线性六面体减缩积分三维实体单元C3D8R［13-14］，钢筋采用两结点线性三维桁架单元T3D2［15］，将钢筋骨架、预应力筋及型钢嵌入到混凝土部件中，忽略钢筋与混凝土间的粘结滑移。为防止梁支座处、梁上端加载面以及预应力筋的端部出现应力集中 ，建模时设置了厚度为20 mm的钢垫块。垫块的弹性模量取为普通钢筋的10倍，采用C3D8R单元。

2　有限元计算结果分析

2.1计算结果与试验结果对比

以PSRCB-01为例，比较试验所得荷载-位移曲线与ABAQUS计算所得的荷载-位移曲线，如图3所示 ，两曲线趋势基本一致，在混凝土开裂前两曲线吻合较好，混凝土开裂后，由于本模型未考虑各钢筋与混凝土间的粘结滑移，使构件刚度增大，同时垫块刚度取值较大也会增加构件的刚度。构件达到极限承载力之后，模型中钢筋与混凝土间的粘结力仍较大，受压区混凝土没有立刻退出工作，故ABAQUS计算所得的荷载-位移曲线在达到极限承载力之后不是骤然下降的。由表3可知:有限元模型计算所得的开裂荷载、屈服荷载、极限荷载与试验所得相应荷载相对误差均值分别为0.153，0.024，0.042，相对误差方差分别为0.00509，0.00022，0.00040，波动较小，证明了此ABAQUS有限元模型在计算预应力型钢超高强混凝土梁承载力方面的有效性和正确性。

图3　PSRCB-01与B-01荷载-位移曲线对比

表3　试验结果与数值模拟计算结果对比

2.2 各梁受弯破坏形态

ABAQUS模型计算出的各预应力型钢超高强混凝土梁的荷载-位移曲线如图4所示，各梁的开裂荷载、屈服荷载和极限荷载见表4。

表4　开裂荷载、屈服荷载及极限荷载的模拟值

由图4可知，预应力型钢超高强混凝土梁受力过程大致可分成四个阶段:加载到混凝土开裂，混凝土开裂到纵向受拉钢筋屈服，纵向受拉钢筋屈服到受压区混凝土被压碎和梁达到极限承载力之后。

混凝土开裂前，纵向钢筋、型钢、预应力筋和混凝土的应变均较小，梁处于弹性变形阶段，荷载-位移曲线呈直线。混凝土开裂后，受拉区混凝土退出工作，梁刚度减小，在荷载-位移曲线上表现为斜率减小、出现第一个拐点但仍呈直线。纵向受拉钢筋屈服后，梁挠度增加较快，型钢屈服部分由下翼缘逐渐向上延伸，梁处于弹塑性工作阶段。混凝土压碎时，梁达到极限承载力。高强混凝土具有明显脆性，混凝土被压碎、崩落后，梁的承载力明显下降，但由于钢骨的存在，梁仍具有一定的承载能力。

2.3各研究因素对承载力的影响

2.3.1 加入型钢的影响

在图4（a）中，由PSRCB-03与PCB-10的荷载-位移曲线对比可知，加入型钢后，构件的初始刚度无明显变化，即加入型钢对混凝土的开裂几乎无影响。混凝土开裂后，PSRCB-03的承载力增长较快，梁刚度较大，极限承载力较PCB-10增加约为23.1%。达到极限承载力之后，承载力显著下降，但由于型钢的存在，梁仍有较大的承载力，弥补了超高强混凝土梁高脆性的缺陷。

图4　梁的荷载-位移曲线

2.3.2 纵向受拉钢筋配筋率的影响

PSRCB-01～PSRCB-03的纵向受拉钢筋配筋率分别为 ρ=0.57%、ρ=0.96%和ρ=1.44%。由表4及图4（b）可知，增加纵向受拉钢筋配筋率对混凝土的开裂几乎没有影响，但使组合梁的屈服荷载和极限荷载增加。纵向受压钢筋配筋率的增加对承载力的影响不大，但能改善构件达到极限状态后的持载能力，综合考虑经济因素 ，不建议通过增加受压钢筋配筋率来改善构件延性。

2.3.3 型钢位置的影响

型钢居中时，位置定义为0，向上偏移定义为负，向下偏移定义为正。由表4和图5可知，仅型钢向下偏移30 mm时，梁的屈服荷载、极限荷载分别增加5.3%、5.1%，达到极限荷载时的挠度减小8.3%。当型钢和预应力筋同时向下偏移30 mm时，梁的屈服荷载和极限荷载增加更多，分别为7.6%，8.8%，达到极限荷载的跨中挠度几乎无变化。当型钢向上偏移30 mm时，梁的屈服荷载和极限荷载分别减小6.3%、1.4%，达到极限荷载时的跨中挠度明显增大。由此可知，型钢向上偏移虽不能提高构件的承载力，不能充分利用钢筋的受拉性能，但可以很好的改善梁的受力性能，提高延性。

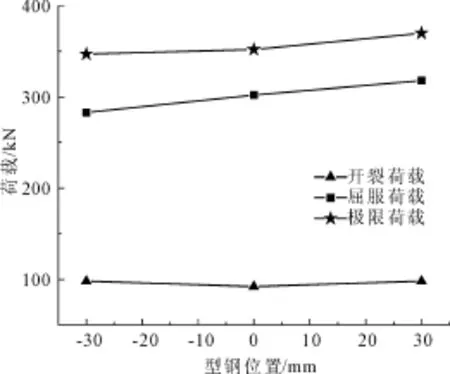
图5　型钢位置对承载力的影响

2.3.4 型钢含钢率的影响

由图4（d）可知，增加型钢尺寸，由I16代替I14，型钢含钢率由4.05%增大为4.91%，使得构件开裂荷载、屈服荷载和极限荷载分别增加8.7%，8.3% 和10.2%，达到极限状态之后的变形能力也有较大提高。

2.3.5 预应力筋配筋率的影响

由图6知，当预应力筋配筋率由0.505%减小到0.356%时，梁的开裂荷载、屈服荷载和极限荷载分别减小14.4%，12.9%和13.4%。由图4（d）可以看出，预应力筋配筋率对梁开裂影响较大 ，较高的预应力筋配筋率能较好的延缓构件的开裂，并使梁具有更高的承载能力。

图6　预应力筋配筋率对承载力的影响

3　结 论

（1）本文利用ABAQUS损伤塑性模型对预应力型钢超高强混凝土组合梁进行非线性分析，模型计算结果与试验结果吻合较好，证明了用ABAQUS对其进行数值分析的正确性。但本模型忽略了型钢、纵筋、预应力筋、箍筋与混凝土之间的粘结滑移，使数值模型中梁的刚度偏大。

（2）预应力型钢超高强混凝土梁受力过程大致可分成四个阶段:开始加载到混凝土开裂，混凝土开裂到纵向受拉钢筋屈服，纵向受拉钢筋屈服到受压区混凝土压碎及梁达到极限承载力之后。

（3）由梁的荷载-位移曲线可知，加入型钢能较好的改善超高强混凝土组合梁高脆性的缺陷 ，型钢位置对组合梁的受力性能有较大影响。预应力筋配筋率对组合梁的开裂荷载影响较大，较高的预应力筋配筋率能延缓构件的开裂。

参考文献:

［1］ 傅传国，李玉莹，梁书亭.预应力型钢混凝土简支梁受弯性能试验研究［J］.建筑结构学报，2007，28（3）:63-73.

［2］ 孟 刚，贾金青，朱伟庆.预应力型钢超高强混凝土梁抗弯性能试验研究［J］.工程力学，2014，31（5）:203-210.

［3］ 贾金青，孟 刚，朱伟庆.预应力型钢超高强混凝土组合梁受弯性能实验研究及承载能力分析［J］.建筑结构学报 ，2014，35（9）:1-10.

［4］ 王建波，贾金青，孟 刚.预应力钢骨超高强混凝土梁抗弯性能非线性分析［J］.水利与建筑工程学报，2012，10（4）:18-21.

［5］ 蒲心诚.超高强高性能混凝土［M］.重庆:重庆大学出版社 ，2004.

［6］ 蒲心诚，王志军，王 冲，等.超高强高性能混凝土的力学性能研究［J］.建筑结构学报 ，2002，23（6）:49-55.

［7］ Shady H S，Khalid M H，Tarek K H，et al.Experimental behavior of prestressed high strength concrete beams［J］.Scientific Research，2013:26-31.

［8］ 蒲心诚，王志军，王 冲 ，等.超高强高性能混凝土的力学性能研究［J］.建筑结构学报，2002，23（6）:49-55.

［9］ 王永威，蒲心诚，王志军 .单轴压力下56.3～164.9MPa混凝土应力 -应变关系［J］.建筑结构学报，2005，25 （1）:97-102.

［10］ 中华人民共和国住房和城乡建设部.中华人民共和国国家质量监督检验检疫总局 .GB50010-2010.混凝土结构设计规范［S］.北京:中国建筑工业出版社，2010.

［11］ 余志武，丁发兴 .混凝土受压力学性能统一计算方法［J］.建筑结构学报，2003，24（4）:41-46.

［12］ 丁发兴，余志武.混凝土受拉力学性能统一计算方法［J］.华中科技大学学报:城市科学版，2004，21（3）:29-34.

［13］ 张 劲，王庆扬 ，胡守营，等.ABAQUS混凝土损伤塑形模型参数验证［J］.建筑结构，2008，38（8）:127-130.

［14］ 梁兴文，钱 磊，谭丽娜.基于ABAQUS的混凝土损伤塑性模型本构关系研究［C］//全国地震工程学术会议论文集.重庆，2010.

［15］ 王 强 ，朱丽丽，李 哲，等.用于ABAQUS显示分析梁单元的钢筋本构模型研究［J］.土木工程学报 ，2013，46（S2）:100-105.

中图分类号:TU375.1

文献标识码:A

文章编号:1672—1144（2015）01—0065—05

DOI:10.3969/j.issn.1672-1144.2015.01.014

收稿日期 :2014-09-26修稿日期:2014-10-21

基金项目 :国家自然基金资助项目（51078059）

作者简介 :孟 笑（1990—），女，山东菏泽人，硕士研究生，研究方向为钢-混凝土组合结构受力性能分析。E-mail:mengxiaodlut@163.com

FEM Analysis on the Flexural Behaviour of Prestressed Steel Reinforced Ultra-high-strength Concrete Beams

MENG Xiao，JIA Jin-qing，WANG Yao-bo，WANG Dong-lai
（Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

Abstract:For the further research on flexural behavior of prestressed steel reinforced ultra-high-strength concrete beams，ABAQUS was used to simulate the scenario when this concrete beam was under stress.The load-displacement curve of the model constructed using ABAQUS was consistent with the experimental result，which proved the accuracy of the finite element model.The results indicate that high ratio of longitudinal reinforcement can enhance the yield load and ultimate load，but has little influence on the cracking.Downward vertical displacement of the section steel can increase yield load and ultimate load，whereas the upward displacement can’t，but it improves the ductility of the beam.Increasing the reinforcement ratio of the prestressed steel can delay the cracking of the components.

Keywords:prestress；section steel；ultra-high-strength concrete；ABAQUS；flexural behavior