参数自整定模糊PI控制器设计与仿真

周 洵 文小玲 邹艳华

（武汉工程大学 电气信息学院，湖北 武汉 430205）

在自动控制领域里，PI 控制方法是目前运用最广泛、最成熟的控制方法， 根据其理论设计出的控制器已经应用到各种工业和生活环境中。 目前大多数是通过大量实验数据来分析选取Kp、Ki， 或者依靠经验来选择合适参数，而且获得的数据还需要不断修正，使得设计过程较为繁琐。 所以，控制器的参数是设计控制器的关键[1]。

模糊控制是用语言变量来描述系统特征， 并依据系统的动态响应和模糊控制规则进行推理以获得合适的控制量，因而具有较强的鲁棒性，但控制精度较小。 本文在传统PI 控制方法的基础上，结合模糊控制理论，设计了一种参数自调节模糊PI 控制方法。 它可以利用模糊逻辑推理对PI 控制器的参数进行在线修正。 这种控制方法能充分发挥模糊控制与PI 控制的优点，具有动态响应快、超调小、静态误差小等特点。 选取某电力电子装置的数学模型来对这两种方法进行仿真实验对比，检验模糊PI 控制器的控制品质。

1 传统PI 控制

PI 控制器是一种线性控制器，它根据系统给定值r（t）与输出量y（t）构成误差信号e（t），其控制器输出信号u（t）同时成比例地反映输入误差信号e（t）和它的积分，即：

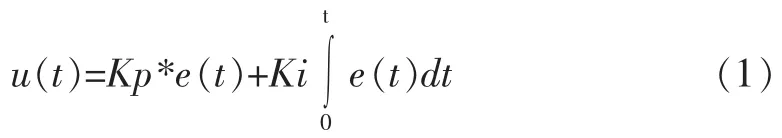
式中，Kp、Ki 为比例和积分系数，两者都是可调的。

其比例部分的作用是反映系统的误差， 加快系统响应速度；积分部分的作用是尽量减小系统的稳态误差，提高系统的稳定性。

2 参数自调整模糊PI 控制

2.1 模糊PI 模型控制原理

模糊控制器的维数过低， 所获得的系统动态性能较差；维数过高，虽在理论方面能获得较好的动态性能，但维数的增加将导致模糊推理运算量增加， 使推理时间变长。所以合理地选择模糊控制器的维数是很重要的[2]。 根据系统变量，考虑综合性能，本文设计了一个二维模糊控制器，该控制器以误差e 和误差变化率ec=de/dt 为控制器的输入变量，以PI 参数变化量ΔKp、ΔKi 为输出量。 通过运用模糊逻辑推理理论， 建立起输入和输出量之间的函数关系：ΔKp=u（e，ec），ΔKi=v（e，ec）。根据控制对象的响应情况对参数自动修正，直到系统稳定。 其原理如图1 所示。

2.2.2 模糊控制规则表的建立

参数自整定过程中需要考虑参数在不同时刻之间的相互关系。 下文归纳总结了在控制过程中不同的e 和ec及PI 参数Kp、Ki 的自整定规则[4]。

2.2.2.1 若误差e 比较大， 为加快系统响应速度，应取较大的Kp、Ki，以达到快速缩小误差的目的。 当然也不能取得过大，否则会造成系统震荡。

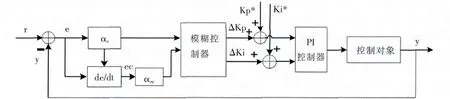
图1 参数自整定模糊PI 控制原理图

参数自整定PI 控制器表达式如下：

PI 控制器输出为：Kp=Kp*+ΔKp，Ki=Ki*+Δki。 其中Kp*、Ki* 分别为PI 控制器Kp、Ki 参数初始值[2]，ΔKp、ΔKi为模糊控制器的输出值。 对于输入量e、ec， 以及输出量ΔKp、ΔKi， 在模糊控制器前后都需要依照系统的具体情况进行尺度变换，获得量化因子和输出因子[3]。

2.2 参数自整定模糊PI 控制器设计

2.2.1 模糊变量论域及隶属函数的选择

设定模糊输入变量e、ec 的模糊论域均为[-3，3]，将其量化为7 个等级{-3，-2，-1，0，1，2，3}。 设定输出变量ΔKp 的模糊论域为[-0.3，0.3]， 并将其量化为7 个等级{-0.3，-0.2，-0.1，0，0.1，0.2，0.3}。 设定输出变量ΔKi 的模糊论域为[-0.06，0.06]，并将其量化为7 个等级{-0.06，-0.04，-0.02，0，0.02，0.04，0.06}。 模糊变量的语言值集合均可设定为{NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大）}。 其中NB 采用S 形隶属度函数，PB 采用Z 形隶属度函数， 其他语言变量采用三角形隶属度函数， 在MATLAB 中确定e、ec 和ΔKp、ΔKi 隶属度函数曲线。 图2 所示为e 的隶属度函数曲线，其它三个变量绘制过程相同。

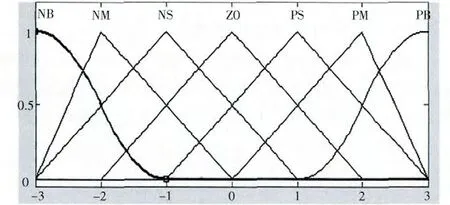
图2 e 隶属度函数曲线

2.2.2.2 若误差e 适中，分两种情况。 当e 和ec 同号时， 被控量朝着偏离给定值的方向变化，Kp、Ki 值应取稍大些；当e 和ec 异号时，被控量朝着接近给定值的方向变化，在这种情况下应逐渐减小Kp 和Ki 的值。

2.2.2.3 当系统误差e 较小或误差为零时，为缩短系统的调节时间，可取适中的Kp，较小的Ki。

模糊控制器设计的关键是建立模糊控制规则表，双输入双输出的模糊控制器的控制规则总共有98 条，其语言描述格式采用“if...then...”。 结合上文所述自整定规则，将其绘制成ΔKp/ΔKi 模糊规则表，如下表1 所示。

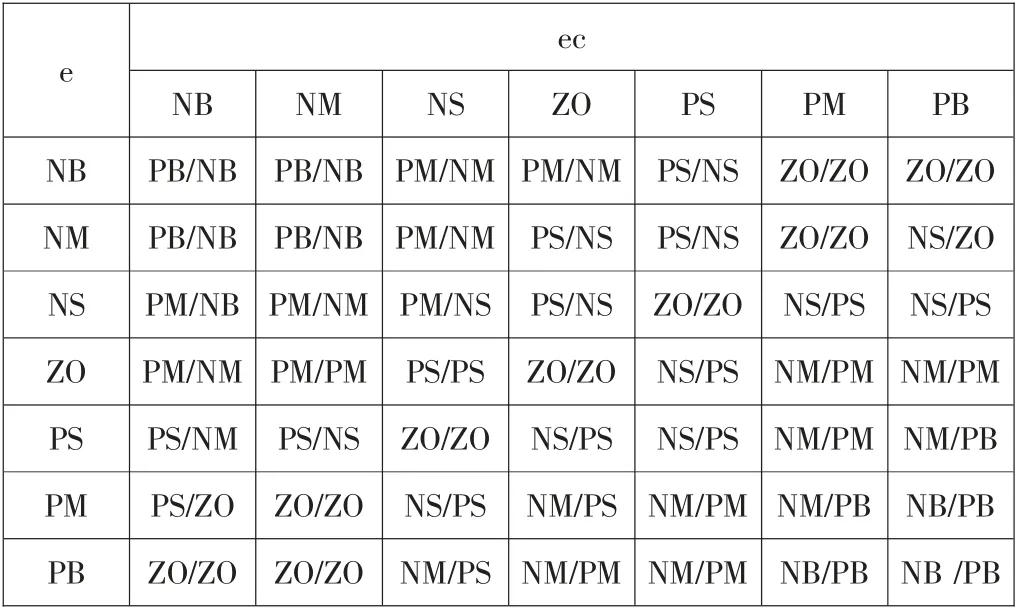
表1 ΔKp/ΔKi 的模糊控制规则

2.2.3 模糊推理运算及清晰化

在模糊控制理论中，模糊推理是模糊决策的前提，是形成模糊控制规则的理论依据。 本文采用Mamdani 推理法，它在模糊控制中是使用广泛的重要方法。 清晰化是将模糊控制器输出的模糊值转化为具体数值， 一般常用的有面积中心法、面积平分法、最大隶属度法。 本文采用面积中心法，较适合隶属度函数是对称情况。

2.2.4 参数自整定设计过程

根据前文对控制规则的建立和设计步骤的详细介绍，其设计流程如图3 所示。

图3 参数自整定模糊PI 控制流程图

图中，e（k）、ec（k）为给定值在第k 个采样时刻的误差和误差差值。

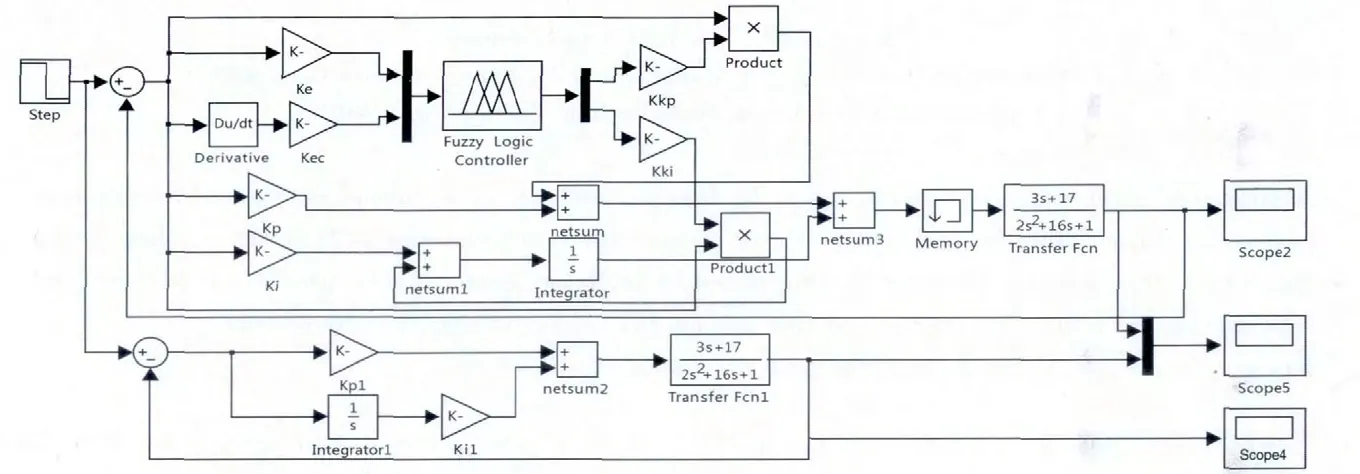
图4 PI 控制和模糊PI 控制系统仿真图

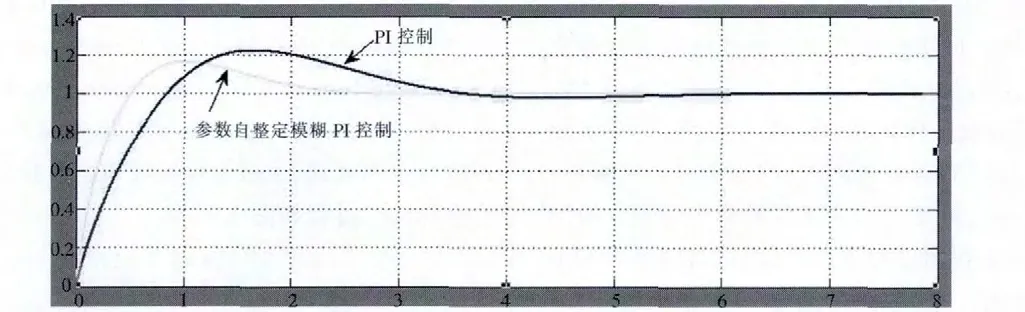
图5 两种控制方法下的系统响应曲线

3 仿真实验结果与分析

根据系统控制要求设置好各个模块的参数， 依照原理图在SIMULINK 平台下搭建好仿真实验图形， 如图4所示。 两种控制器在相同的被控对象下进行仿真实验，选取被控系统—二阶环节为控制对象。

在单位阶跃响应下观察系统响应曲线，波形图如图5所示。 可以看出，参数自整定模糊PI 控制方法在2.5s 就趋于稳定， 而PI 控制方法在6s 以后才逐渐趋于稳定，明显前者响应速度更快。 而且前者的超调量更小，最大超调量只有PI 控制方法的40%，动态特性更好。 从而证实了本文设计的参数自整定模糊PI 控制方法具有良好的动静态特性，控制效果能达到系统反映要求。

4 结 语

传统PI 控制器参数的整定一直是其设计的难点，本文在PI 控制的基础上结合模糊控制的特点， 设计了参数自整定模糊PI 控制器，提高了系统的动态特性、鲁棒性，并且降低超调量， 同时保留了PI 控制对系统稳态误差的解决能力。 仿真结果证明该控制方法具有响应速度快、超调小、静态误差小等优点，说明该控制器具有一定的实用价值。

［1］黄友悦，曲立国.PID 控制器参数整定与实现［M］.北京：科学出版社，2010.

［2］何继爱， 田亚菲. 模糊自适应整定PID 控制及其仿真［J］．甘肃科学学报，2004，16（1）：63-66.

［3］王川川，赵锦成，齐晓慧.模糊控制器设计中量化因子、比例因子的选择［J］.四川兵工学报，2009，30（1）：61-63.

［4］沈承，黄光宏，曹世宏，等.PID 控制系统的参数调节技巧［J］.机械工程与自动化，2008（4）：155-156.