Compressive Strength Estimation for the Fiber－Reinforced Polymer(FRP)－Confined Concrete Columns with Different Shapes Using Artificial Neural Networks

CAO Yu－gui(曹玉贵)，LI Xiao－qing(李小青)，HU Jun(胡 隽)

College of Civil Engineering and Mechanics，Huazhong University of Science and Technology，Wuhan 430074，China

Compressive Strength Estimation for the Fiber－Reinforced Polymer(FRP)－Confined Concrete Columns with Different Shapes Using Artificial Neural Networks

CAO Yu－gui(曹玉贵)*，LI Xiao－qing(李小青)，HU Jun(胡 隽)

College of Civil Engineering and Mechanics，Huazhong University of Science and Technology，Wuhan 430074，China

An evaluation of existing strength of concrete columns confined with fiber-reinforced polymer(FRP)was presented with extensive collection ofexperimentaldata． According to the evaluation results，artificial neural networks(ANNs)model to predict the ultimate strength of FRP confined column with different shapes was proposed．The models had seven inputs including the column length，the tensile strength of the FRP in the hoop direction，the total thickness of FRP，the diameter of the concrete specimen，the elastic modulus of FRP，the corner radius and the concrete compressive strength．The compressive strength of the confined concrete was the output data．The results reveal that the proposed models havegood prediction and generalization capacitywith acceptable errors．

compressive strength;concrete column;artificial neural networks(ANN);fiber-reinforced polymer(FRP)

Introduction

The use of fiber－reinforced polymer(FRP)in retrofitting damaged structures or strengthening existing structures has been extensively studied in recent years．In order to get the ultimate strength of FRP confined concrete column，many stress－strain models have been proposed［1－7］．Most of models were used to calculate circular columns，and few models were used to predict the rectangular and square columns．All of those models are regressed from test data．Using a limited test data is one of the weaknesses of existing models in which further applicability of their approaches may not be guaranteed［8］．Because the ultimate strength of FRP confined concrete is affected by many factors and parameters．

At present，artificialneuralnetworks(ANNs) have occasionally been used to predict the compressive strength of FRP confined concrete［9］．Because ANN can get high accuracy results based on a large number of experimental data．Körogˇlu et al．［10］developed a combined neural network model for the estimation of the flexural capacities of the quadrilateral FRP－confined reinforced concrete(RC)columns．The proposed model was found to be quite successful for both FRP confined and unconfined columns．Tanarslan et al．［11］developed an ANN model to predict the shear capacity of RC beams，retrofitted in shear by means of externally bonded wrapped and U－jacketed FRP．The neural network results are compared with some guidelines．Performed analysis showed that the neural network model was more accurate than the guideline equations with respect to the experimental results．Naderpour et al．［12］also used ANN method to predict the FRP－confined compressive strength of concrete．The simulated results also have a good precision．However，none of the existing ANN models can satisfactorily capture the ultimate strength of FRP confined concrete columns with different shapes．

To address this gap in the research，the authors have collected large number of experimental data and analytical investigations of the ultimate strength of FRP－confined columns with different shapes，such as circular，square，and rectangular columns．In this paper，the ANN model for FRP－confined concrete that is applicable to circular，square，and rectangular columns is proposed．The ANN model results agree well with the experiment results［13－15］．

1 Existing Ultimate Strength Models

Before discussing the ANN method，a few ultimate strength models that are related to this work are reviewed．They can predict different types cross section，including circular，square，and rectangular columns，at the same time．

1)Samaan et al．model［1］

The model proposed by Samaan et al．is given by

where f'cuand f'coare the compressive strengths of the confined and the unconfined concrete，respectively;flis the lateral confining pressure; k1is the confinement effectiveness coefficient，;ks=2r/d is the shape factor，in which d is the diameter of an equivalent circular column and is equated to the side length of a square column or the longer side length in the case of a rectangular section;r is the corner radius of crosssection;εfrpis taken as the ultimate tensile strain;tfrpis the thickness of FRP;and Efrpis the elastic modulus of FRP in the hoop direction．

2)ACI 440 model［16］

The ACI 440 model(ACI 2002)adopted the following Eq．(3)，which was originally proposed by Mander et al．［17］for steel confined concrete columns，

In this model，the confining pressure is given as

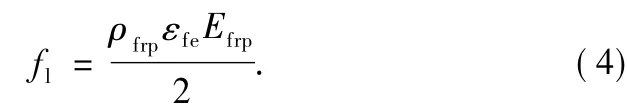
Here ρfrpis the FRP volumetric ratio and can be determined by

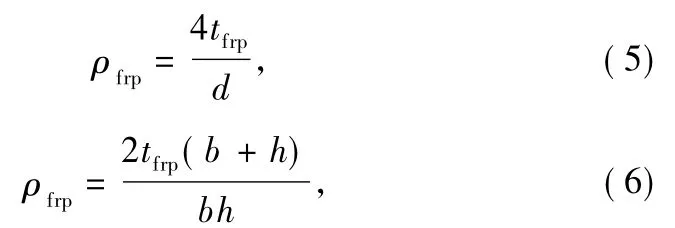
where Eq．(5)is for circular sections，and Eq．(6)is for noncircular sections．

The nominal hoop rupture strain in the FRP jacket isassumed to be equal to an effective value(εfe)，and it is specified that for RC column members that are completely wrapped by the FRP system around the cross section，the maximum strain used for the design should be limited to 0．4%，that is

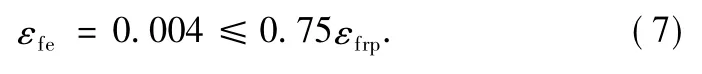
Here，ksis the shape factor，for circular section ks=1，for square and rectangular sections，

The confining effect of FRP jackets should be assumed to be negligible forrectangularsectionswith aspectratiosb/h exceeding 1．5 or face dimensions，b or h，exceeding 900 mm，unless testing demonstrates their effectiveness．

3)Youssef et al．model［7］

The following strength model is proposed，depending on the geometry of the cross－section:

For circular sections

for rectangular sections

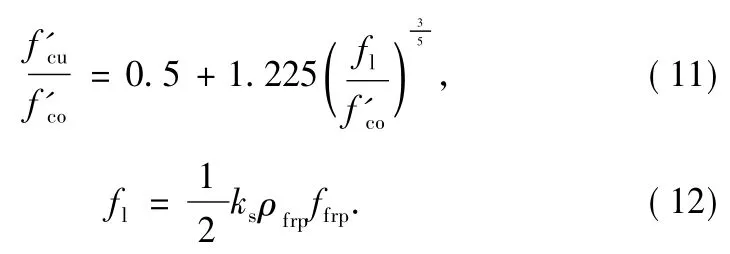
Here，d is egual to the side length of a square column or the longer side length in the case of a rectangular section;ksis the shape factor，for rectangular column，

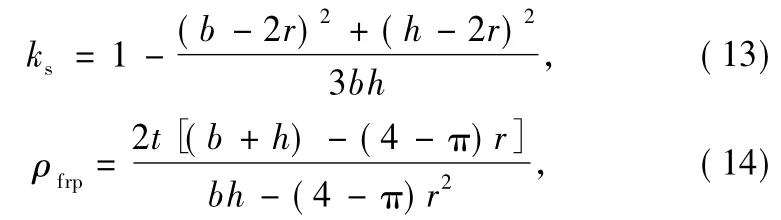
where b and h are the width and the depth of the cross－section，respectively．

4)Wei and Wu model［18］

The ultimate stress can be assumed to take the following form:

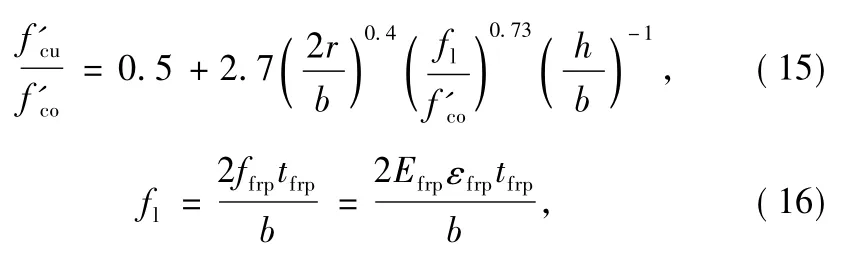
where，b is the width of the column，and h is equal to the diameter of circular columns or the length of the smaller side of rectangular columns．

2 Evaluation of Existing Models

The criterion used in this work to evaluate the performance of a model is the root mean square error(RMSE)．RMSE is a quadratic scoring rule which measures the average magnitude of the error．It gives a relatively high weight to large errors．This means the RMSE is the most useful when large errors are particularly undesirable．In addition，RMSE values are also useful to determine how close theoretical results get to the experimental results．

where，eiis the difference between calculated and experimental results and n is the number of data that is used for calculation，fe－cuis the strength value getting from experiment，and fp－cuis the strength value getting from the existing model and ANN model．

A most comprehensive and updated database containing the test results of 53 FRP wrapped plain concrete column including，circular columns，square columns，and rectangular columns are assembled in this work from the open literature in Table 1．All of the fiber sheets that were used in the database were unidirectional and wrapped in the hoop direction only，so that the FRP jacket only acted as a confinement mechanism and had an insignificant stiffness in the axial direction．

Table 1 Material properties of the experimental specimens

(Table 1 Continued)

The performances of the four existing models with RMSE value are given in Fig．1．Among those the model proposed by Wu and Wei model in the form of

is found to fit the database best，with the lowest value of 8．85，while Samaan et al．model is 9．12，the ACI 440 model is 14．59，and the Youssef et al．Model is 13．31．

Fig．1 Performance of existing models for different cross section columns

In the literature，it is a common practice for three different models to be used for the circular columns，the square columns and the rectangular columns．However，it is quite natural and logical that a confined concrete model for square columns with an arbitrary corner radius should degenerate into a model for circular columns when 2r/b =1．When the cross－sectional aspect ratio，h/b，is equal to 1，the rectangular columns become a square columns．When 2r/b and h/b are equal to 1，the column cross－section is circular．So the parameters of r，b，and h are very important for a unified strength model．In the proposed model，the parameters of r，b，and h are used，and the input parameters are chosen based on Eq．(15)．

3 Neural Network Modeling

3．1 AAN

In orderto providesufficientdatabase fortraining，verifying，and testing of neural networks，the database contains 599 test results，which is collected form published papers［19－41］．In the database，seven parameters are as input nodes:(1)the total thickness of FRP(tfrp)in mm;(2)the diameter of the concrete specimen(d)in mm;If the specimen cross section is rectangular or square，b and h are the short and long side dimension，respectively，as illustrated in Fig．2;(3) the specimen length(L)in mm;(4)the elastic modulus of FRP(Efrp)in MPa;(5)the corner radius(r)in mm;(6)the compressive strength of the unconfined concrete(fco)in MPa; (7)the compressive strength of the confined concrete(fc'c)in MPa is used as the target node．

The network architecture for the prediction of compressive strength of FRP－confined concrete column is given in Fig．3．The network architecture consists of one input layer，one hidden layer，and one output layer．The input layer includes seven neurons，hidden layer has twelve neurons and the output layer has one neuron．The network is trained using levenberg－marquardt back propagation algorithm．Before training the selected data，normalization/scaling for the whole data is made．This is done since log－sigmoid transfer function is used in the network which recognizes values between 0 and 1．Equation(19)is used to scale the data from 0．2 to 0．8，the minimum and the maximum values are taken to use linear relationship between those values．

Fig．2 The column shapes

Fig．3 Schematic diagram of ANN model

Development of ANN model is carried out as follows:

(1)database selection and pre－processing;

(2)selection of model inputs;

(3)selection of model geometry;

(4)model training;

(5)model validation．

The criterion for stopping the training of the networks is mean square error(MSE)，which is the average squared difference between outputs and targets．Lower values mean better performance of the network(zero means no error)．Figure 4 shows the MSE of the network starting at a large value and decreasing to a small value．In other words，it shows that the network is learning．The total training time was 16，and the best validation performance and MSE of training data were all bellow 10－2．MSE of test samples and valid data were about 0．01．Regression values(R－values)measure the correlation between outputs and targets in the networks．An R－value of 1 means a close relationship and in contrast，and 0 means a random relationship．These two criteria(MSE and R－values) were considered as the basis for selecting the idealized network．The regressions of training，validation，and test data simulated by ANN model are summarized in Fig．5．

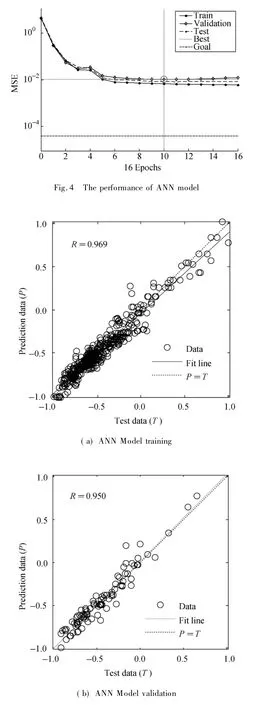
Fig．5 Regressions of training，validation，and test data simulated by ANN model

3．2 Comparison of ANN strength results withtesting results

Fig．6 Performance of ANN model

The ultimate strength of experimental，ANN prediction and theoretical results are listed in Figs．6－7．It can be observed that there is good performance of the neural network in predicting the experimental results．RMSE result of ANN is 7．89，which is the best value，compared with the calculated theoretical results．The length of column is considered in ANN model，which is not considered at other existing models，so the network predictions are generally more satisfactory than those given by traditional regression equations．

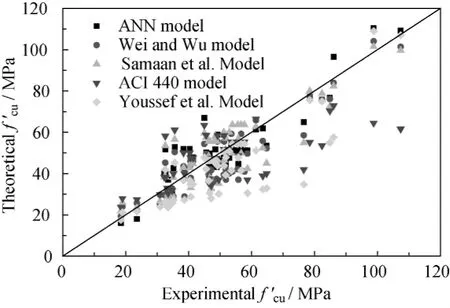
Fig．7 Performance of all the models

4 Conclusions

(1)The Youssef et al．model and ACI model give conservative valuesforcircular，square， and rectangular columns，and Wei and Wu model is the most accurate compared with other existing model．The lowest RMSE value of 8．85，while the Samaan et al．model is 9．12，ACI 440 model is 14．59，and Youssef et al．Model is 13．31．

(2)An ANN strength model for FRP－confined concrete columns with different shapes has been presented herein．This model buildsup a relationship between the seven input parameters and one output parameterwith twelvehidden neurons．One of the advantages of this model is its unified form prediction．There are rare studies in the literature in which the application of one ANN is demonstrated on prediction ultimate strength of FRP confined concrete．In order to verify the performance of the network，the results from ANN simulations was compared with the results of existing strength model，RMSE result of ANN is 7．89，which is the best value．All of outcomes emphasizes that the obtained ANN results have good agreement with the experimental results and the calculated theoretical results．

［1］Samaan M，Mirmiran A，Shahawy M．Model of Concrete Confined by Fiber Composites［J］．Journal of Structural Engineering，1998，124(9):1025－1031．

［2］Moran D A，Pantelides C P．Stress－Strain Model for Fiber Reinforced Polymer Confined Concrete ［J］． Journalof Composites for Construction，2002，6(4):233－240．

［3］Xiao Y，Wu H．Compressive Behavior of Concrete Confined by Various Types of FRP Composites Jackets［J］．Journal of Reinforced Plastics and Composites，2003，22(13):1187－1202．

［4］Toutanji H，Saafi M．Stress－Strain Behavior of Concrete Columns Confined with Hybrid Composite Materials［J］．Materials and Structures，2002，35(6):338－347．

［5］Lam L，Teng J G．Design Oriented Stress－Strain Model for FRPConfined Concrete in Rectangular Columns［J］．Journal of Reinforced Plastics and Composites，2003，22(13):1149－1186．

［6］Teng J G，Jiang T，Lam L et al．Refinement of a Design－Oriented Stress－Strain Model for FRP Confined Concrete［J］．Journal of Composites for Construction，2009，13(4):268－278．

［7］Youssef M N，Feng Q，Mosallam A S．Stress－Strain Model for Concrete Confined by FRP Composites［J］．Composites Part B: Engineering，2007，38(5):614－628．

［8］Naderpour H，Kheyroddin A，Ghodrati A G．Prediction of FRPConfined Compressive Strength ofConcreteUsing Artificial Neural Networks［J］．Composite Structures，2010，92(12):2817－2829．

［9］Duan Z H，Kou S C，Poon C S．Prediction of Compressive Strength of Recycled Aggregate Concrete Using Artificial Neural Networks［J］．Construction and Building Materials，2013，40: 1200－1206．

［10］Körogˇlu M A，Ceylan M，Arslan M H，et al．Estimation of Flexural Capacity of Quadrilateral FRP－Confined RC Columns Using Combined Artificial Neural Network［J］．Engineering Structures，2012，42:23－32．

［11］Tanarslan H M，Secer M，Kumanlioglu A．An Approach for Estimating the Capacity of RC Beams Strengthened in Shear with FRP Reinforcements Using Artificial Neural Networks［J］．Construction and Building Materials，2012，30:556－568．

［12］Naderpour H，Kheyroddin A，Amiri G G．Prediction of FRPConfined Compressive Strength ofConcrete Using Artificial Neural Networks［J］．Composite Structures，2010，92(12): 2817－2829．

［13］Ilki A，Kumbasar N．Compressive Behaviour of Carbon Fibre Composite Jacketed Concrete with Circular and Non－circular Cross－Sections［J］．Journal of Earthquake Engineering，2003，7 (3):381－406．

［14］Tao Z，Yu Q，Zhong Y Z．Compressive Behaviour of CFRPConfined Rectangular Concrete Columns［J］．Magazineof Concrete Research，2008，60(10):735－745．

［15］Wei Y Y．Stress－Strain Behavior ofFRP－Confined Concrete Column［D］．Hongkong，China:University of Hong Kong，2014:130－136．

［16］American Concrete Institute(ACI)Committee 440．(2002)．Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures［S］．

［17］Mander J B，Priestley M J，Park R．Theoretical Stress－strain Model forConfined Concrete［J］． JournalofStructural Engineering，1998，114(8):1804－1826．

［18］Wei Y Y，Wu Y F．Unified Stress－Strain Model of Concrete for FRP Confined Columns［J］． Construction and Building Materials，2012，26(1):381－392．

［19］Wu G，Lü Z T，Wu Z S．Strength and Ductility of Concrete Cylinders Confined with FRP Composites［J］．Construction and Building Materials，2006，20(3):134－148．

［20］Wang L M，Wu Y F．Effect of Corner Radius on the Performance ofCFRP－Confined Square Concrete Columns: Test［J］．Engineering Structures，2008，30(2):493－505．

［21］Watanabe K，Nakamura H，Honda Y．Confinement Effect of FRP Sheet on Strength and Ductility of Concrete Cylinders under Uniaxial Compression［C］．Proceeding of the third international symposium on Non－Metallic(FRP)Reinforcement for Concrete Structure，Tokyo，Japan，1997(1):233－240．

［22］Xiao Y，Wu H．Compressive Behavior of Concrete Confined by Carbon Fiber Composite Jackets［J］．Journal of Materials in Civil Engineering，2000，12(2):139－146．

［23］Lam L，Teng J G．Ultimate Condition of Fiber Reinforced Polymer－Confined Concrete［J］．Journal of Composites for Construction，2004，8(6):539－548．

［24］Lam L，Teng J G，Cheung C H，et al．FRP－Confined Concrete under Axial Cyclic Compression［J］．Cement and Concrete Composites，2006，28(10):949－958．

［25］Jiang T，Teng J G．Analysis－Oriented Stress－Strain Models for FRP－Confined Concrete［J］．Engineering Structures，2007，29 (11):2968－1986．

［26］Saafi M，Toutanji H A，Li Z．Behavior of Concrete Columns Confined with Fiber Reinforced Polymer Tubes［J］．ACI Materials Journal，1999，96(4):500－509．

［27］Berthet J F，Ferrier E，Hamelin P．Compressive Behavior of Concrete Externally Confined by Composite Jackets．Part A，Experimental Study［J］．Construction and Building Materials，2005，19(3):223－232．

［28］Mandal S，Hoskin A，Fam A．Influence of Concrete Strength on Confinement Effectiveness of Fiber－Reinforced Polymer Circular Jackets［J］．ACI Structural Journal，2005，102(3):383－392．

［29］Rochette，P，Labossière，P，AxialTesting ofRectangular Column Models Confined with Composites［J］．Journal of Composites for Construction，2000，4(3):129－136．

［30］Chaallal O，Shahawy M，Hassan M．Performance of Axially Loaded Short Rectangular Columns Strengthened with Carbon Fiber－Reinforced Polymer Wrapping［J］．Journal of Composites for Construction，2003，7(3):200－208．

［31］Rousakis T C，Karabinis A I，Kiousis P D．FRP－Confined Concrete Members，Axial Compression Experiments and Plasticity Modeling［J］．Engineering Structures，2007，29(7):1343－1353．

［32］Wu Y F，Wei Y Y．Effect of Cross－Sectional Aspect Ratio on the Strength of CFRP－Confined Rectangular Concrete Columns［J］．Engineering Structures，2010，32(1):32－45．

［33］Almusallam T H．Behavior of Normal and High－Strength Concrete Cylinders Confined with E－Glass/Epoxy Composite Laminates［J］．Composites Part B:Engineering，2007，38(5/6):629－639．

［34］Benzaid R，Chikh N E，Mesbah H．Behavior of Square Concrete Column Confined with GFRP Composite Wrap［J］．Journal of Civil Engineering and Management，2008，14(2):115－120．

［35］Benzaid R，Mesbah H，Chikh N E．FRP－Confined Concrete Cylinders:Axial Compression Experiments and Strength Model［J］．Journal of Reinforced Plastics and Composites，2010，29 (16):2469－2488．

［36］Mirmiran A，Shahawy M．BehaviorofConcrete Columns Confined by Fiber Composites［J］．Journal of Structural Engineering，1997，123(5):583－590．

［37］Masia M J，Gale T N，Shrive N G．Size Effects in Axially Loaded Square－Section Concrete PrismsStrengthened Using Carbon Fibre Reinforced Polymer Wrapping［J］．Canadian Journal of Civil Engineering，2004，31(1):1－13．

［38］Shahawy M，Mirmiran A，Beitelman T．Tests and Modeling of Carbon－Wrapped Concrete Columns［J］．Composites Part B: Engineering，2000，31(6/7):471－480．

［39］Lin H J，Liao C I．Compressive Strength of Reinforced Concrete Column Confined by CompositeMaterial［J］．Composite Structures，2004，65(2):239－250．

［40］Harries K A，Carey S A．Shape and“Gap”Effects on the Behavior of Variably Confined Concrete［J］．Cement and Concrete Research，2003，33(6):881－890．

［41］Wu H L，Wang Y F，Yu L，etal．Experimentaland ComputationalStudies on High－Strength Concrete Circular Columns Confined by Aramid Fiber－Reinforced Polymer Sheets［J］．Journal of Composites for Construction，2009，13(2):125－134．

TU398

A

1672－5220(2015)03－0395－06

date:2014－04－24

National Natural Science Foundation of China(No．51278391)

*Correspondence should be addressed to CAO Yu－gui，E－mail:caoyugui@163．com