基于全局任务坐标系的二轴电液系统轮廓控制

熊 义，魏建华，冯瑞琳，张 强

（浙江大学 流体传动及机电系统国家重点实验室，浙江 杭州310027）

目前，对于二／多轴电液系统的运动控制研究多为平行轴的同步控制，应用于液压机、液压举升装置等领域［1-4］，鲜有研究涉及更为复杂的电液轴空间轨迹运动控制.

强力旋压机是二轴电液系统空间运动控制的典型应用场合，多属于数控机床，对加工精度要求较高，在国防军工方面发挥着重要作用［5-7］.因此，设计优良的二轴电液系统轮廓运动控制器对于提升强力旋压机的加工性能有着现实意义.

多轴运动轮廓控制一直是数控机床研究中的热点领域，发展大致经历单轴无耦合，多轴简单耦合和基于轮廓误差估算模型的任务坐标系3 个阶段［8-11］.Yao等［12-14］提出了轮廓误差的精确估算模型，并基于此构建了正交全局任务坐标系，然后直接针对该坐标系中的轮廓误差与跟踪误差设计了二轴直线电机系统的自适应鲁棒轮廓运动控制器，获得了理想的控制效果.

一方面，全局任务坐标系能够精确计算轮廓误差；另一方面自适应鲁棒控制器可以有效地应对电液系统中存在的各种非线性、参数不确定性和不确定非线性［15-16］.基于以上考虑，本文将把基于全局任务坐标系的自适应鲁棒控制方法扩展应用于具有更高阶系统动力学的电液系统，并通过实验验证所设计控制器的轮廓控制性能.

1 正交全局任务坐标系

如图1所示，在笛卡尔坐标空间中存在期望曲线

Pc0是期望曲线的起点.假设空间存在一点Po1（可以在空间任意位置），点Po1沿穿过其的期望曲线法线投影到期望曲线上的位置为点Pc1.Pc1是期望轮廓曲线上与Po1之间距离最近的点，它们之间的距离rc1即为Po1相对于期望曲线的轮廓误差，而rm1则是Po1沿期望曲线相对于起始点Pc0的曲线长度，形象地反映了Po1的“跟踪路程”.在Pc1处分别沿外法线方向与曲线前进的切线方向定义单位矢量Irc1和Irm1.这是一对正交的单位矢量，并且在期望曲线上的每一点都能定义这样的一对正交矢量，于是可以用这对矢量作为基沿着期望曲线构造一个正交的曲线坐标系.原来笛卡尔坐标系中的任意一个空间点在新的曲线坐标系中的坐标均可以用轮廓误差与跟踪路程来表示，如Po1的坐标为（rc1Irc1，rm1Irm1）.该曲线坐标系只与期望曲线的形状有关，其坐标反映了轮廓任务与跟踪任务，它在轴系对期望轮廓曲线的跟踪过程中是时变的，并且把原来的笛卡尔坐标耦合在一起.

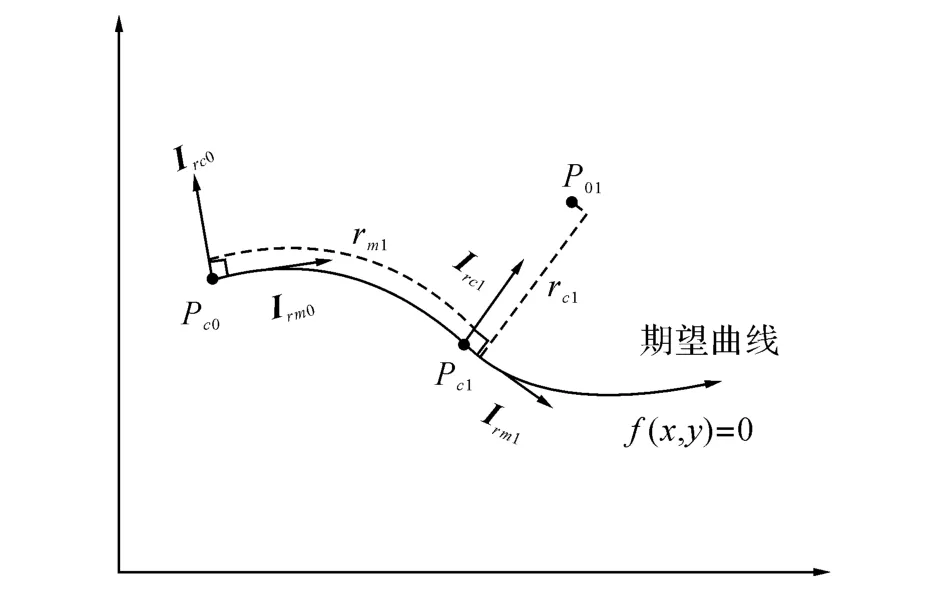
图1 正交全局任务坐标Fig.1 Orthogonal global task coordinate

把期望轮廓曲线用变量ζ∈R 参数化表示

式中：xζ（ζ），yζ（ζ）是2个关于ζ的已知函数，

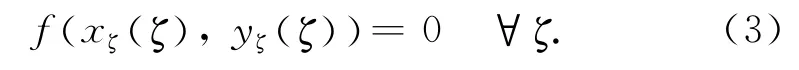
其中xζ（ζ）存在反函数

于是从轮廓起始点qζ（0）沿轮廓曲线运动到qζ（ζ）的路程为

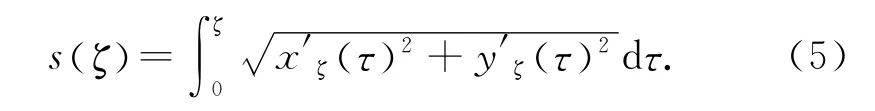
式中：x′ζ＝∂x／∂ζ；y′ζ＝∂y／∂ζ.

正交全局任务坐标系的数学表示为

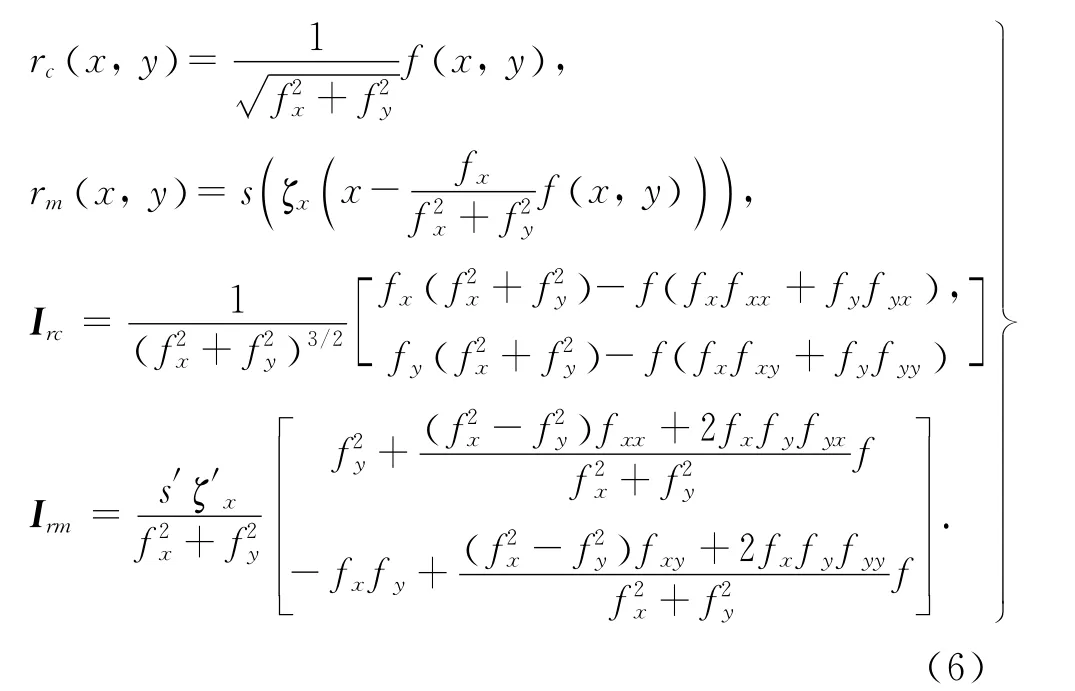
式中：fx＝∂f／∂x，fy＝∂f／∂y，

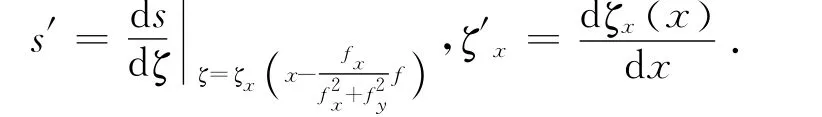
rc（x，y）即为轮廓误差的计算模型.对于正交全局任务坐标系数学表达式（6）的详细推导过程可参见文献［14］.

以圆形作为期望轨迹，其笛卡尔坐标系表达式为

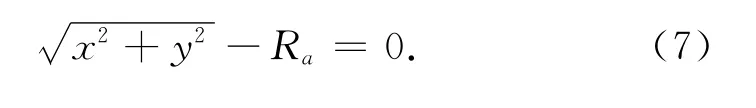
将其参数化表示为

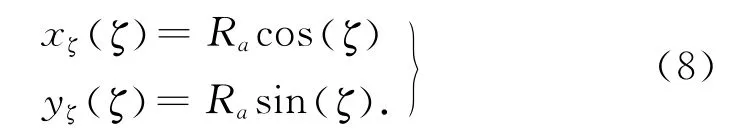
由式（6）可计算得

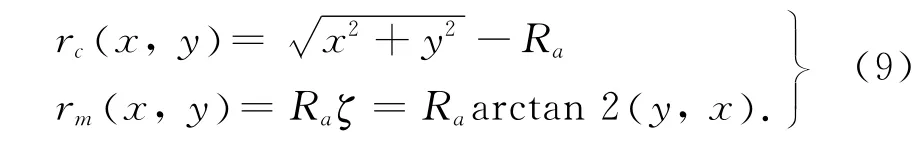
式中：arctan2（y，x）为反正切函数，其值域为［0，2π］.如图2所示是圆形期望轮廓的全局任务坐标.

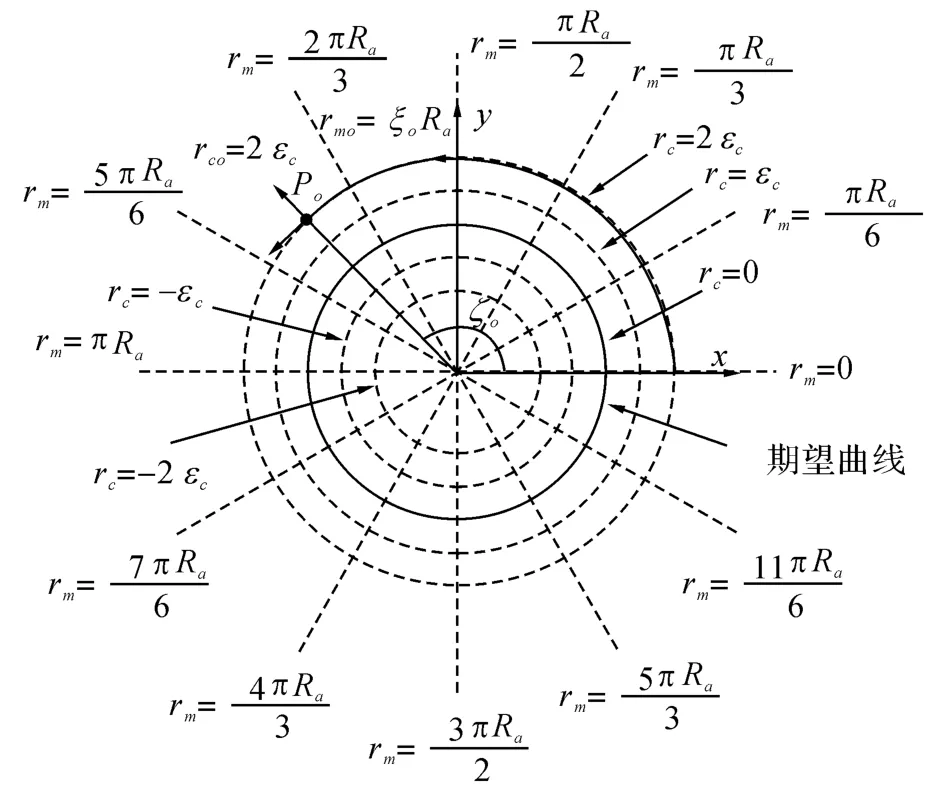
图2 圆形期望轮廓的全局任务坐标Fig.2 Global task coordinates for circular desired contour

2 二轴电液系统动力学模型

本文所研究的二轴电液系统如图3所示，系统配置有3个液压缸：纵向缸与负载缸竖直放置，相对安装于质量块mv两侧，活塞杆均与质量块刚性连接；横向缸安装于质量块上，随质量块一起纵向运动.其中纵向缸与横向缸受高频响阀控制，为驱动缸；负载缸的无杆腔受溢流阀与减压阀控制，提供负载力.

文中用下标·h与·v分别表示·为横向与纵向缸的参数或变量.系统力平衡方程为

式中：mh、mv分别为横、纵向缸驱动负载质量.xh、xv分别为横、纵向缸位移.ph1、ph2分别为横向缸两腔压强.Ah1、Ah2分别为横向缸两腔作用面积.pv1、pv2分别为纵向缸两腔压强.Av1、Av2分别为纵向缸两腔作用面积.kfch、kfcv分别为横、纵向建模库伦摩擦力系数.bh、bv分别为横、纵向建模黏滞阻尼系数.g 为重力加速度.pc为负载缸无杆腔压强.Ac为负载缸无杆腔作用面积.dh、dv分别为横、纵向不确定干扰力.

横、纵向缸的两腔压强动态模型为

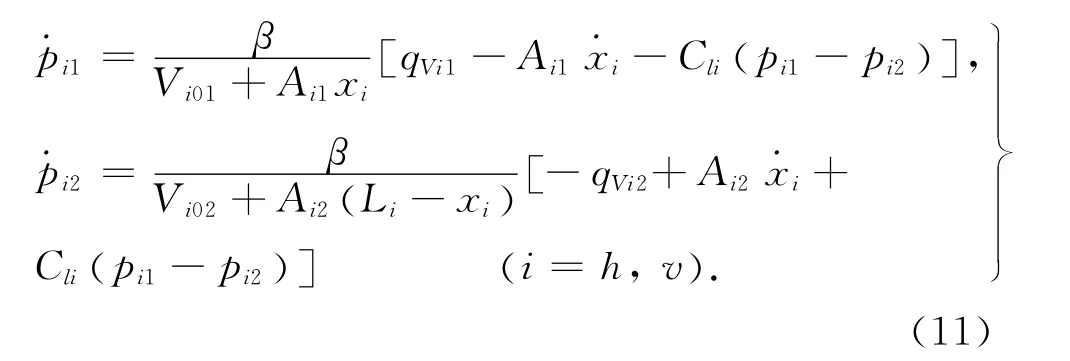
式中：β为液压油体积弹性模量.Cli为横、纵向缸内泄漏系数.Li为横、纵向缸行程.Vi01，Vi02为横、纵向缸两腔死容积.qVi1，qVi2为高频响阀至横、纵向缸两腔流量.

高频响阀 流量qVi1，qVi2的 映射表 达式为

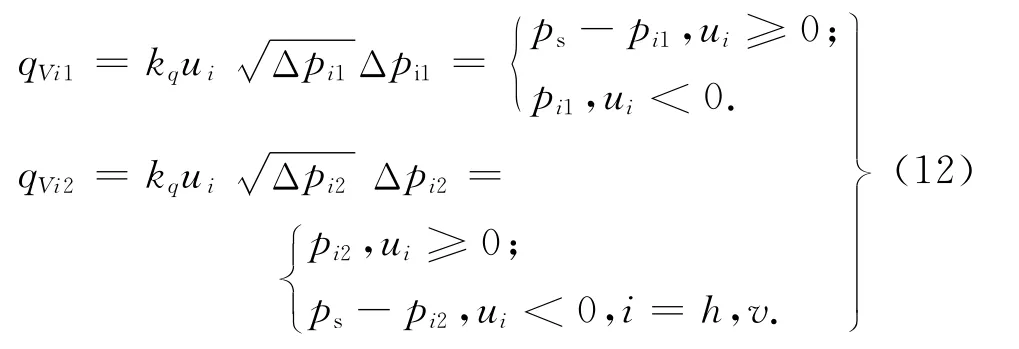
式中：kq为高频响阀综合流量系数，ui为横、纵向高频响阀控制电信号，ps为油源压强.

综合式（10）、（11）与（12），横向缸与纵向缸在笛卡尔空间的动力学模型为

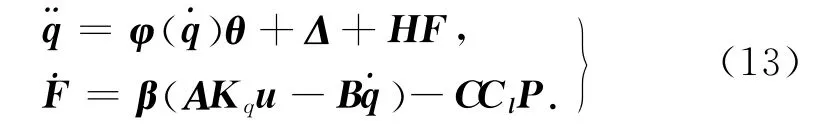
以上2个等式分别为系统的运动动力学模型与驱动力的动态模型.式中：q＝［xh，xv］T.Δ＝［dht／mh，dvt／mv］T.θ，H 分别为不确定参数矢量和矩阵，

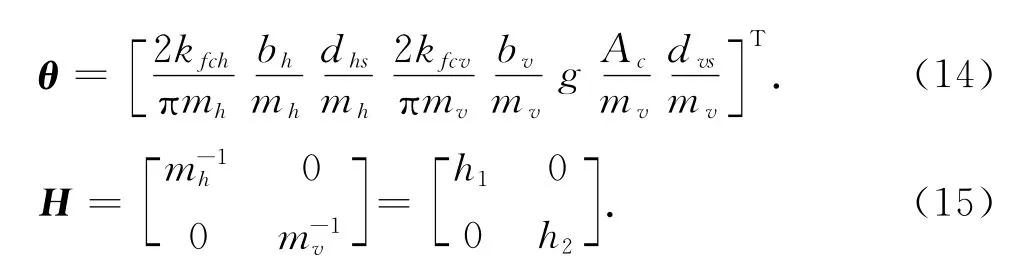
F＝［Fh，Fv］T＝［ph1Ah1-ph2Ah2，pv1Av1-pv2Av2］T，是横、纵向缸的驱动力矢量.用E 表示2×2单位矩阵，β＝βE，Kq＝kqE.u＝［uh，uv］T.P＝［ph1-ph2，pv1-pv2］T.di＝dis＋dit（i＝h，v），dis和dit分别为di的慢时变分量与快时变分量.A、B、C和Cl均为2×2矩阵，表达式分别为

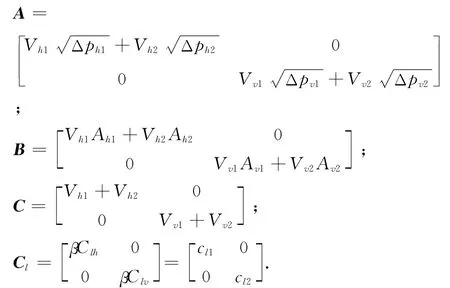
式中：

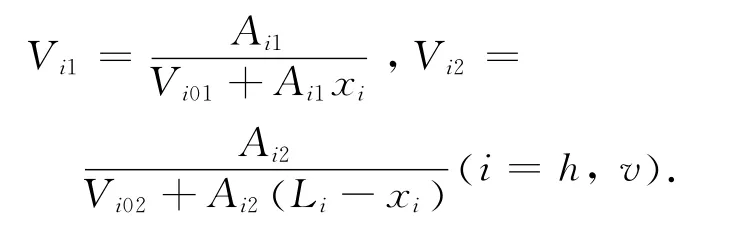
显然，A、B、C 和Cl都是对角正定矩阵.

令r＝［rc，rm］T表示q的曲线坐标，有

雅克比矩阵J＝［Irc，Irm］T，Irc与Irm用式（6）计算.动力学模型（13）中的运动部分在正交全局任务坐标系内的表达式为

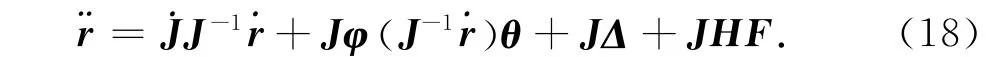
除θ 与H 外，β，Cli也作为不确定参数处理.下文中·i表示矢量·的第i个分量，·imax与·imin分别指·i的最大值与最小值.

假设1：系统中的不确定参数及不确定非线性的边界是确定的，满足

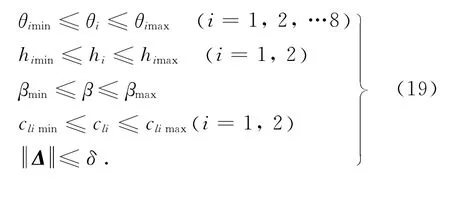
3 控制器设计

1.1 参数自适应律

式中：χ代表各参数的自适应函数.自适应律（20）满足［14］

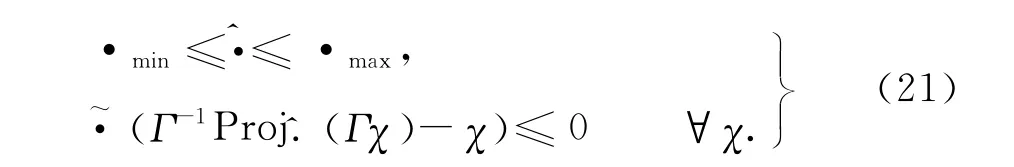
式中：Γ 为自适应速率，为正实数.

1.2 轮廓运动控制器设计

在任务空间内规划的期望轨迹的曲线坐标为rd＝［rcd，rmd］T，rcd为轮廓误差的期望，所以rcd≡0.机床的进给速度多为恒速，所以令rmd＝fmdt，fmd是一个常数，t为时间.

定义任务空间内的误差矢量为er＝r-rd＝［ec，em］T，其滑模切换面为s＝＋Kc1er.Kc1是一个正定的对角反馈增益矩阵，Kc1＝diag｛［kc1r，kc1m］T｝.下文中若·表示矢量，diag｛·｝表示以矢量·的分量依次作为对角元素构造对角矩阵的数学运算；若·表示对角矩阵，diag｛·｝表示以矩阵·的对角元素依次作为分量构造矢量的数学运算.

引理1：一个n×n 的对角矩阵G 与一个n×1的矢量v满足

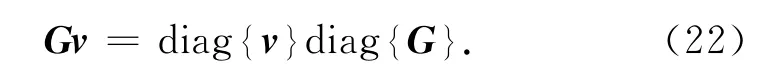
定义半正定Lyapunov函数

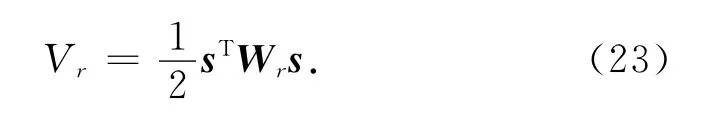
式中：Wr＝diag｛［wrc，wrm］T｝，是一个对角正定常数矩阵.式（23）的时间导数为构造非线性控制函数矢量Fr＝［Frh，Frv］T和自适应调整函数τθ1、τh1为

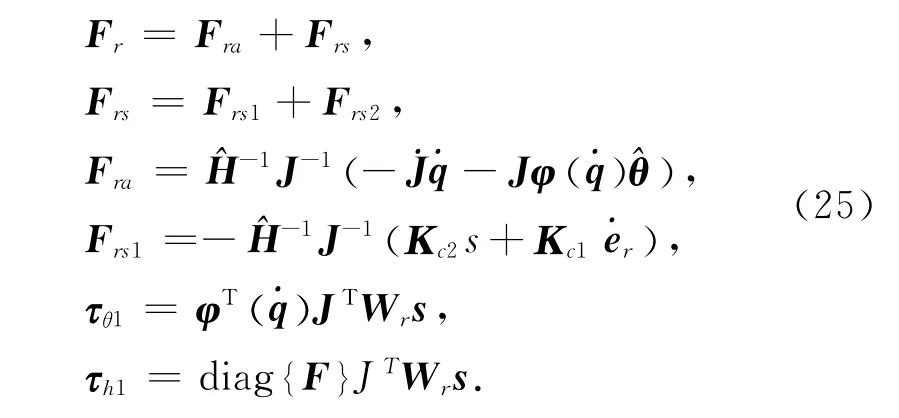
式中：控制函数矢量Fr为系统驱动力矢量F 的期望.Fra为其中的自适应模型补偿项，对建模库伦摩擦力和建模黏滞阻力等进行补偿，同时自适应机制在线修正其中的不确定参数以实现精确补偿.Frs为鲁棒控制项，包含Frs1与Frs22部分.Frs1为名义镇定部分，包含了任务误差矢量er的比例反馈与微分反馈.Kc2＝Kc2c＋Kc2s，是Frs1中对角正定的反馈控制增益矩阵.Kc2c＝diag｛［kc2r，kc2m］T｝，是对角正定常数矩阵.Kc2s则满足

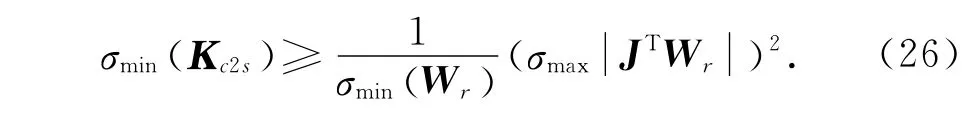
式中：σmin（·）与σmax（·）分别为求矩阵·的最小与最大特征值.σmax｜·｜是求矩阵·特征值绝对值的最大值（谱半径）.Frs2的作用是应对系统中的建模偏差与不确定非线性，是光滑的函数矢量，满足

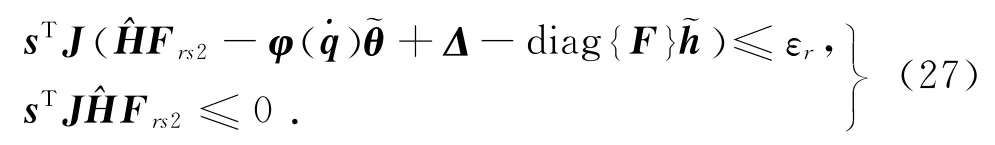
式中：εr为正的控制器设计参数，表征了er收敛域的边 界.Frs2可 以 以s 的 非 线 性 反 馈 实 现［14］.h＝diag｛H｝.令F 与Fr的偏差为eF＝F-Fr，将式（25）代入式（24）得

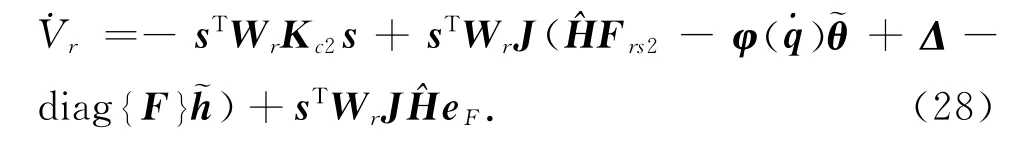
式（28）中等号右边的第1项是耗散的，第2项是有界或耗散的，若要˙Vr是有界或耗散的，eF必须是收敛的.接下来综合系统的实际控制输入实现eF的收敛.

定义半正定Lyapunov函数

式中：WF＝diag｛［wFh，wFv］T｝，是一个对角正定常数矩阵.式（29）的时间导数为

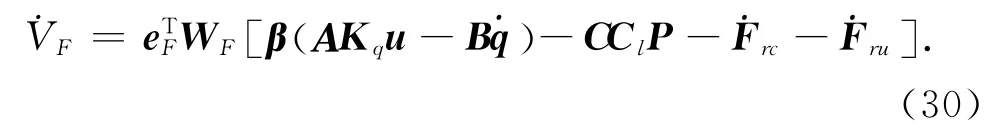
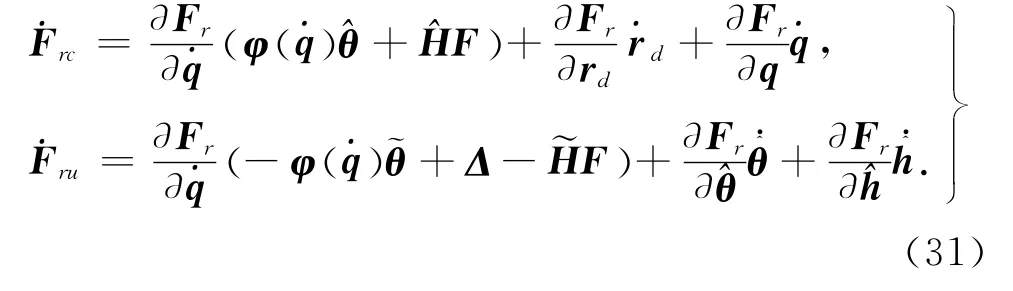
设计系统的实际控制输入u，以及自适应调整函数τθ2，τh2，τβ和τcl为

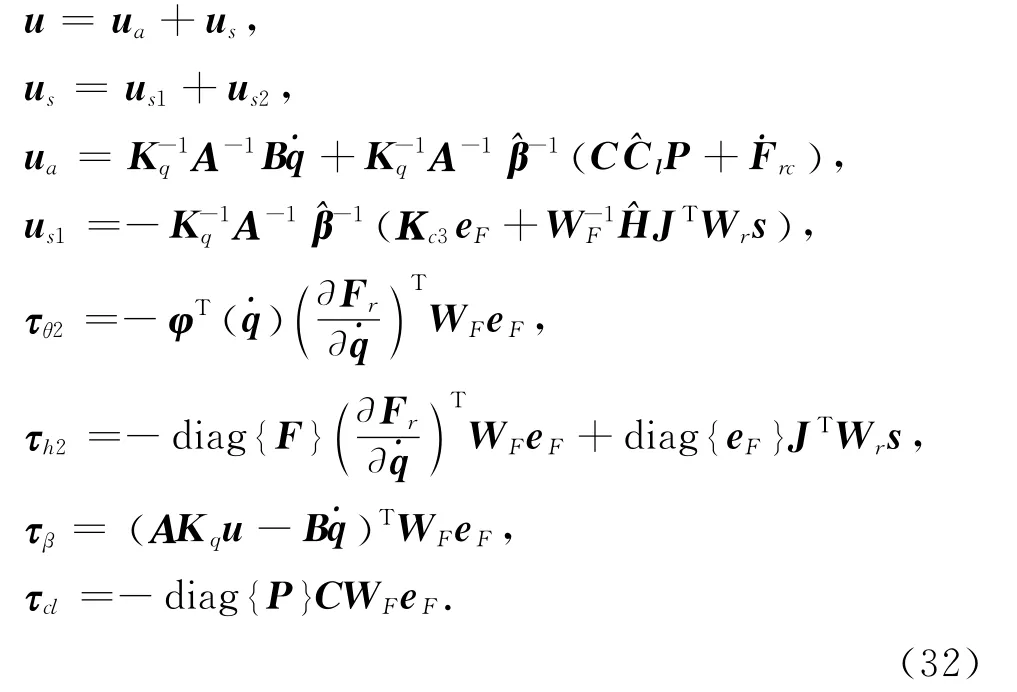
与Fr类似，控制函数矢量u 也包含模型补偿项ua与鲁棒控制项us.ua在自适应机制的作用下精确补偿了液压缸容腔在运动中因体积变化、泄漏和压强动态变化而产生的流量.us中的us1为名义镇定项，包括控制力偏差和任务误差滑模的比例反馈.其中Kc3＝Kc3c＋Kc3s，为反馈控制增益，为对角正定矩阵.Kc3c＝diag｛［kc3h，kc3v］T｝，为对角正定常数矩阵.Kc3s满足

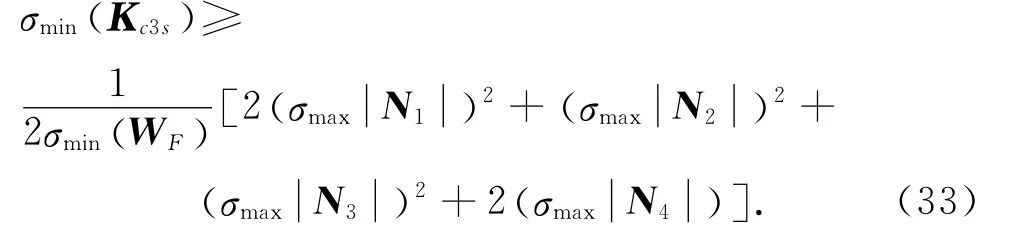
us2控制了˙Fr中的不确定非线性，为光滑的函数矢量，满足

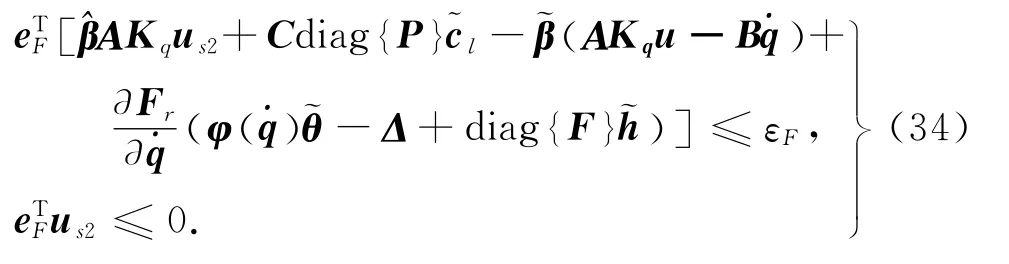
式中：εF为正的控制器设计参数，表征eF收敛域的边界.us2可以是eF的非线性反馈.cl＝diag｛Cl｝.将式（32）代入式（30）得到

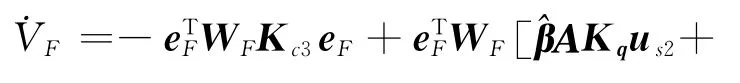
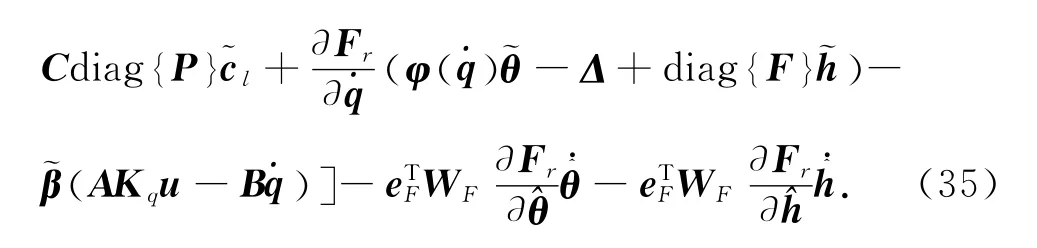
系统的自适应律为

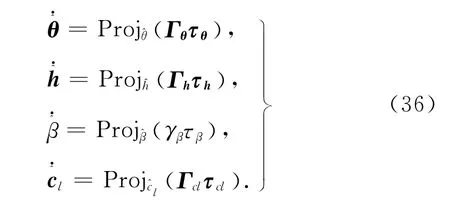
式中：Γθ、Γh、Γcl分别为8×8，2×2和2×2对角正定的自适应速率矩阵.γβ为的自适应速率，为正值.自适应函数τθ＝τθ1＋τθ2，τh＝τh1＋τh2.如图4所示为控制器的原理框图.

定理：对于二轴电液系统（13），在假设1成立的前提下，控制输入用式（32）综合并且采用自适应律（36），可以得到如下结果：

1）系统的全局Lyapunov函数V＝Vr＋VF是指数收敛的，轮廓误差将会被控制在一个确定的范围内.

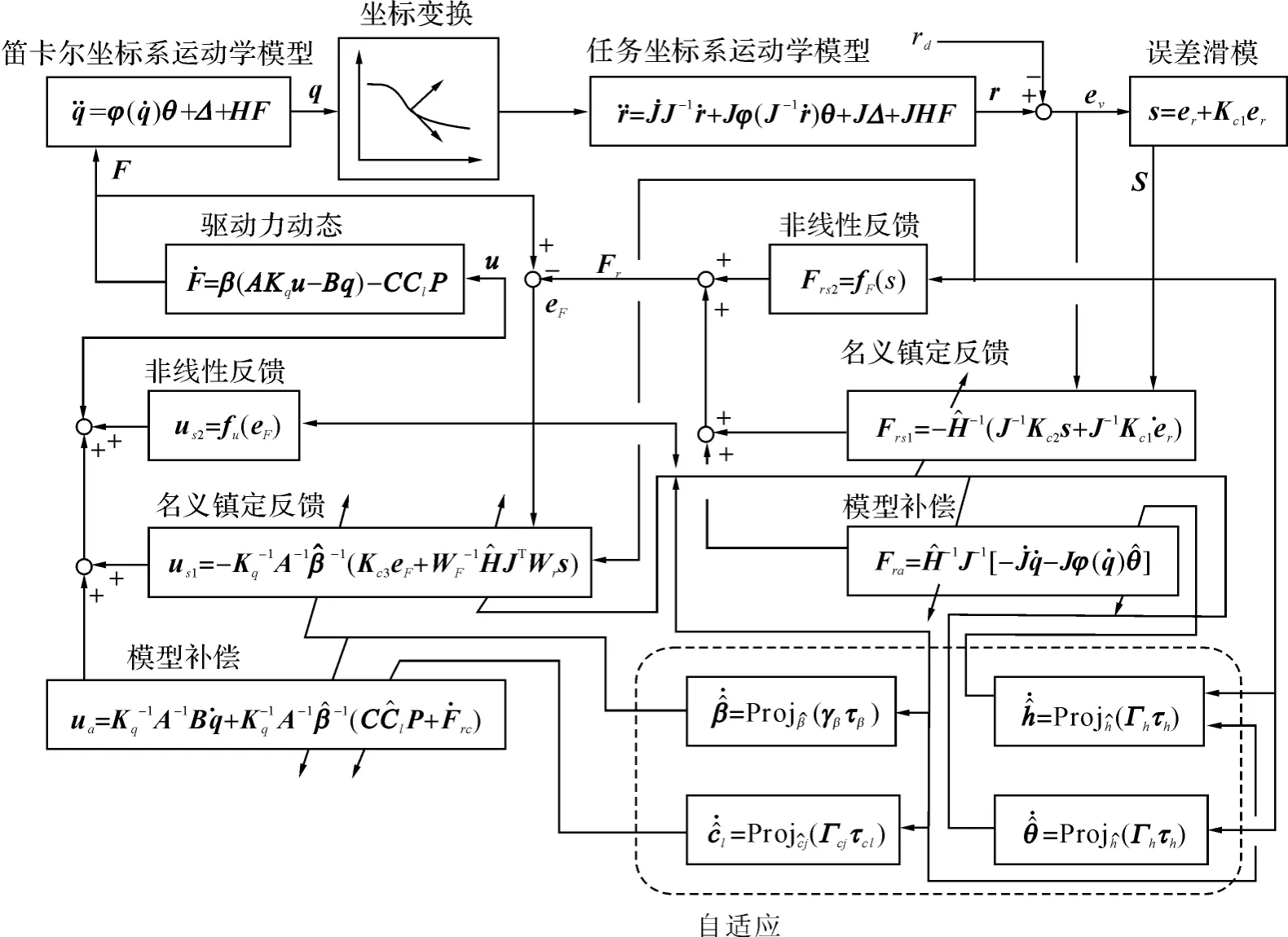
图4 控制器原理框图Fig.4 Principle diagram of controller

2）如果不存在瞬变的不确定非线性，即Δ＝0，系统能够实现对轮廓误差的渐进控制，即当t→∞，rc→0.

证明：将式（28）、（35）代入˙V，并考虑式（27）、（34），可以得到

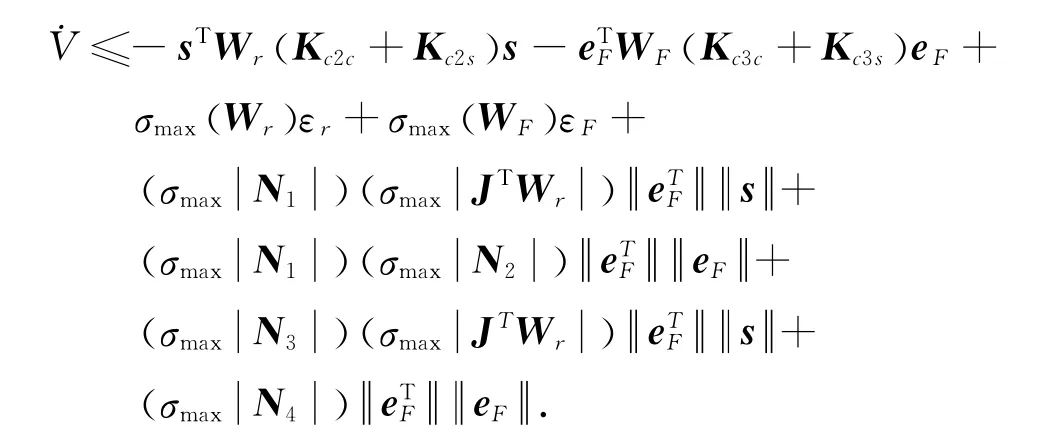
根据式（26）、（33），可推出

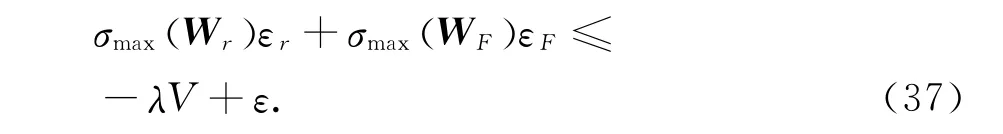
式中：λ＝2min｛σmin（Kc2c），σmin（Kc3c）｝，

ε＝σmax（Wr）εr＋σmax（WF）εF.

式（37）中的矩阵均为正定矩阵，所以λ 与ε 均为正数.利用比较定理可推知

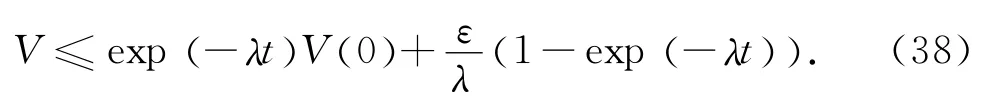
V 将会指数收敛于ε／λ 表征的边界范围内，亦即s，er与eF是有界的，结论（1）得证.假设Δ＝0，重新选择半正定Lyapunov函数

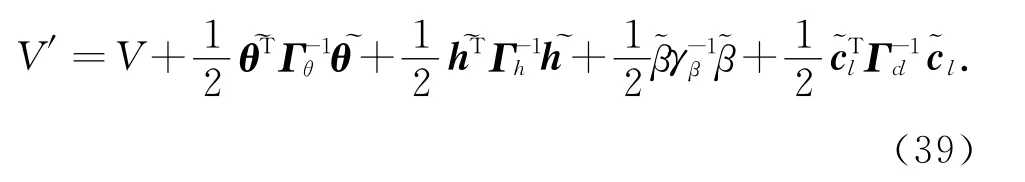
其对时间的导数为

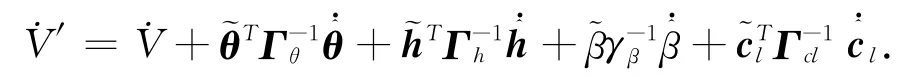
将式（28）、（35）、（36）代入上式，并考虑式（21）、（27）与（34），可以推出

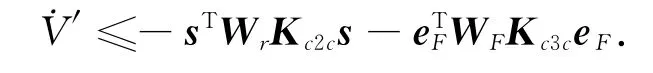
由于s与eF是一致连续的，所以当t→∞时，它们终将趋近于零，结论（2）得证.

说明：在计算式（32）中u 时，可根据AKqu 分量的符号计算矩阵A 从而计算u.

4 实验研究

4.1 实验系统

实验系统的照片如图5所示，原理框架见图6.控制程序在Simulink Real-Time环境下编写并执行，程序运行周期为1 ms.控制信号及传感器信号分别通过NI公司PCI 6259 数据采集卡生成和采集，其数／模与模／数转换器分辨率均为16位.横、纵向缸的位移用磁栅尺测量，分辨率为1μm.泵源压强ps＝7 MPa.2个控制阀均是REXROTH 公司制造的高频响阀，型号为4WRREH6VB40L，其单边压差3.5MPa下的额定流量为40L／min，正弦频响不低于80Hz.

图5 实验系统照片Fig.5 Picture of experiment set

实验对控制器进行了简化：非线性控制函数Frs2与us2被省略，Kc2、Kc3只保留其中的常数部分.在实际应用中并不需要定理中全局收敛的结论，只要保证一定的稳定工作范围即可.在期望轮廓上，曲线任务坐标rc和rm的单位方向矢量分别与期望轮廓上单位法向矢量和单位切向矢量相同，故在期望轮廓附近，雅克比矩阵J 近似简化为［14］

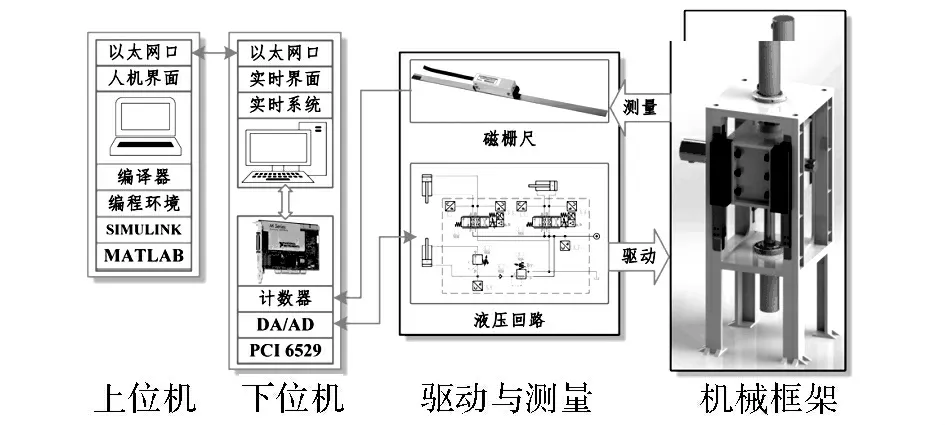
图6 实验系统结构框架Fig.6 Frame structure of experiment set

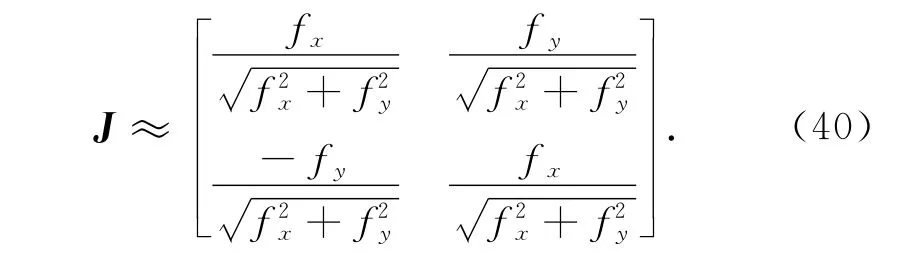
以上简化使控制器更具有实用性.控制器的参数见表1.控制器中估计参数的名义值为θ＝［29.096m／s2，4 579.38s-1，0m／s2，6.3m／s2，379.15s-1，9.8 m／s2，1.122×10-5m2／kg，0 m／s2］T；h＝［0.091 408 kg-1，0.005 714 3 kg-1］T；β＝700 MPa；cl＝［2.123 8×10-4m3／s，2.333 3×10-4m3／s］T.估计参数的上界为θmax＝［37m／s2，5 500 s-1，5m／s2，7m／s2，500s-1，9.8m／s2，1.122×10-5m2／kg，10 m／s2］T；hmax＝［0.1kg-1，0.006 kg-1］T；βmax＝800 MPa；clmax＝［2.3×10-4m3／s，2.5×10-4m3／s］T.估计参数下界为θmin＝［20 m／s2，3 900s-1，5 m／s2，5 m／s2，200s-1，9.8 m／s2，1.122×10-5m2／kg，-10 m／s2］T；hmin＝［0.082kg-1，0.005 2kg-1］T；βmin＝600 MPa；clmin＝［1.9×10-4m3／s，2.1×10-4m3／s］T.

控制器中并未对所有的不确定参数进行估计，未在线估计参数对应的自适应速率设为0.各参数的自适应速率为Γθ＝diag｛［0，1.3×107，4×104，0，5×105，0，0，3×104］T｝；Γh＝diag｛［0.070，0.008］T｝；γβ＝3 000；Γcl＝diag｛［4×10-15，7×10-15］T｝.

表1 控制器参数Tab.1 Controller parameters

4.2 性能指标

为了量化评价控制器的性能，实验分析采用了如下指标评估实验结果：

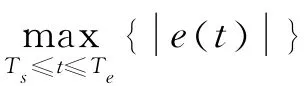
4.3 实验结果分析

为测试所提轮廓控制器的性能，比较了如下2种轮廓控制方法：

C1：本文所提的基于全局任务坐标系自适应鲁棒轮廓运动控制器.

C2：基于交叉耦合［17-18］的自适应鲁棒轮廓运动控制器.C2的原理框图如图7所示，Cx＝sinαex／2R 与Cy＝cosα-ey／2R 分别是横轴与纵轴的耦合控制增益.其中，ex和ey分别是横轴与纵轴的单轴跟踪误差，erc是估算的轮廓误差.α 是轮廓曲线上指令点处切线（沿曲线前进方向）与横坐标轴的夹角（此夹角即为式（6）中单位切向矢量Irm在轮廓曲线上指令点处的方向角）.R 为期望圆轮廓的半径.xd与yd则是横轴与纵轴的期望轨迹.CCC 为交叉耦合控制器，其传递函数为

ARC是每一单轴的自适应鲁棒控制器，其细节可参见文献［15］.

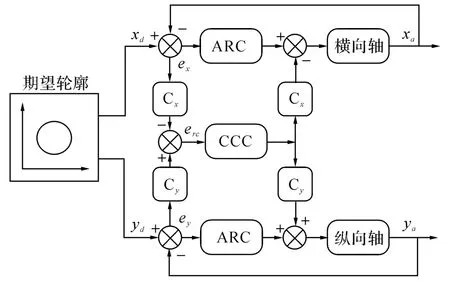
图7 C2原理框图Fig.7 Principle diagram of C2

实验中期望轮廓为圆形，半径为0.04 m，角速度为0.04πrad／s.任务坐标系内期望轮廓任务与期望跟踪任务，以及笛卡尔坐标系内的期望轮廓与横、纵轴的期望轨迹见图8.如图9 所示对比了C1与C2的轮廓误差与单轴跟踪误差，实验结果见表2.如图10所示为期望轮廓与C1、C2跟踪轨迹的局部放大图.

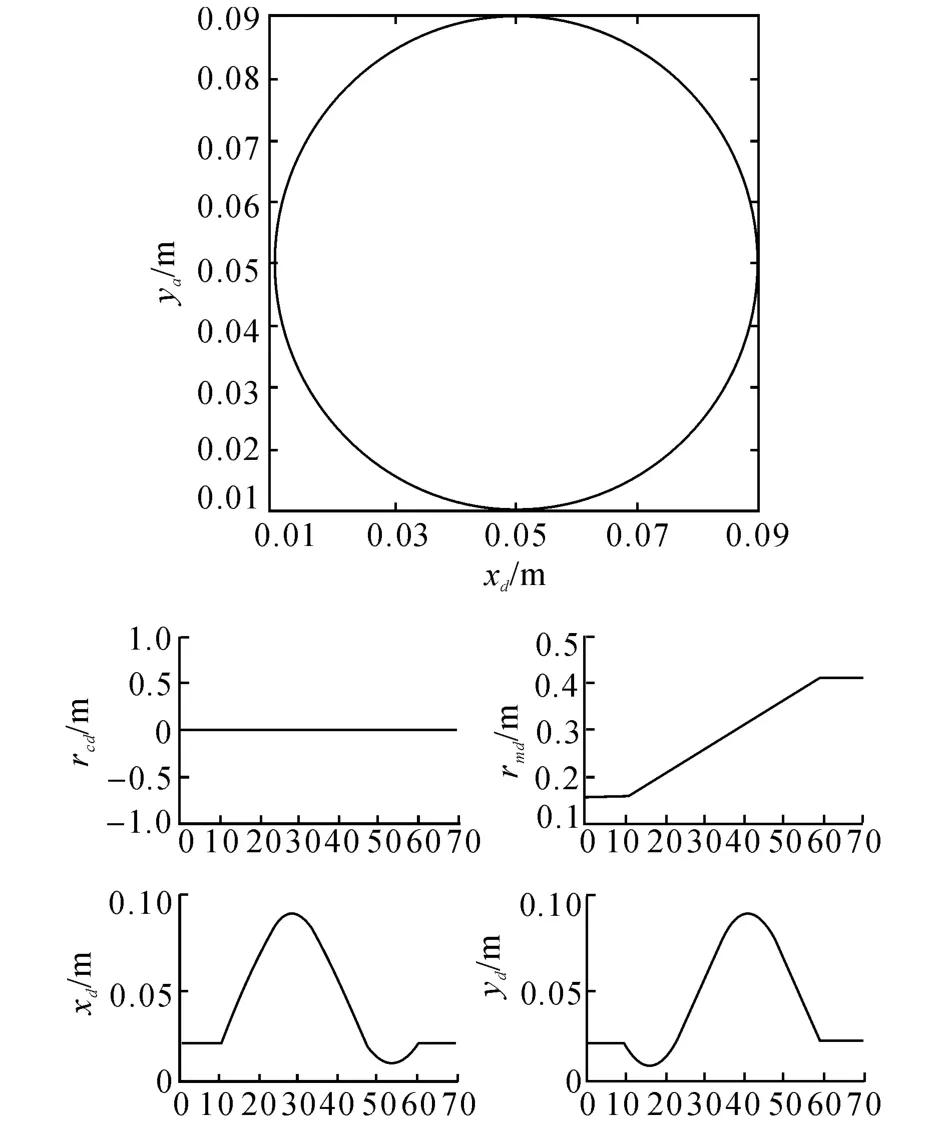
图8 期望轮廓轨迹Fig.8 Desired contour trajectories

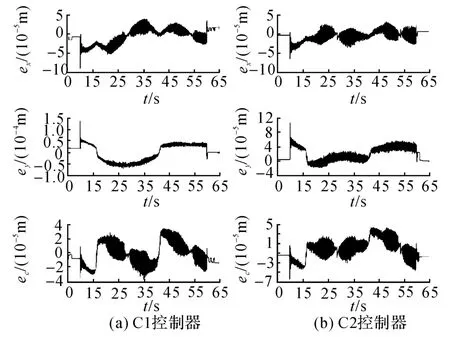
图9 轮廓误差与单轴跟踪误差曲线Fig.9 Contour error and single axis tracking error

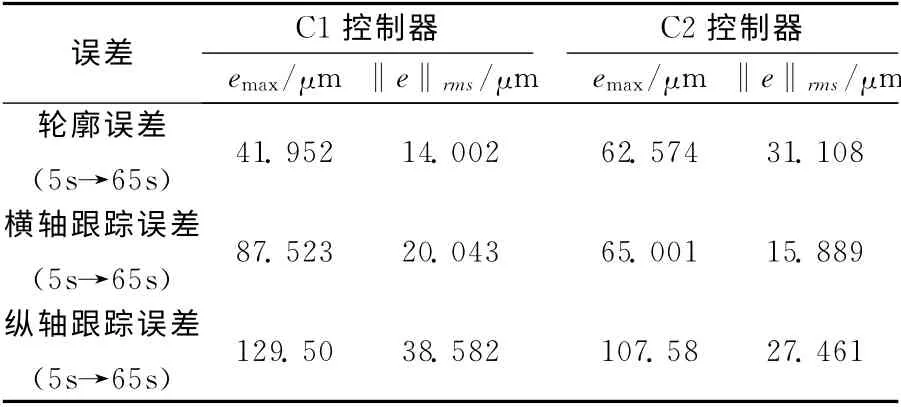
表2 图9中的实验误差Tab.2 Experimental errors in Fig.9

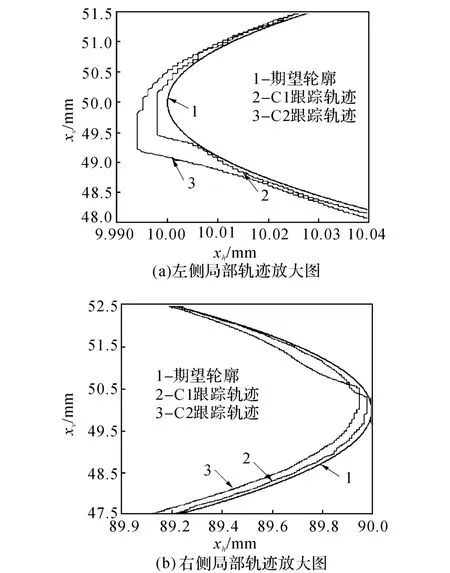
图10 C1与C2跟踪曲线的局部轨迹放大图Fig.10 Partial contours in tracking curves of C1and C2

如图7所示，C2轮廓控制的基本原理是首先通过单轴跟踪误差估计计算轮廓误差，然后依靠对估计轮廓误差的反馈控制以调节两轴的轮廓运动.C2中轮廓误差的估算依赖于单轴跟踪误差，不具备C1对轮廓控制任务与跟踪控制任务的协调能力.因此，从图9以及表2中的数据不难发现，虽然C2实现了优于C1的单轴跟踪控制效果，但其轮廓控制性能却不如C1，协调性较差.如图10所示，在横轴换向运动时，C2轮廓控制性能有更为明显的退化.另外，从C1的设计过程可知，其在运动控制部分的反馈控制参数与控制任务的刚度是直接对应的，与C2相比C1在实际应用中对控制参数整定的指导性更强.

对于C1而言，轮廓控制任务与跟踪控制任务是解耦的，轮廓控制刚度与跟踪控制刚度可以独立调节.为了说明这个特性，实验中测试了具有不同控制参数的C1-2与C1-3控制器，与C1控制器形成对比.C1-2和C1-3控制器中仅参数kc1m与C1不同，其余控制器参数与C1相同.根据前文定义可知参数kc1m是跟踪误差的反馈增益，与跟踪控制刚度 相 关 联.C1-2 中kc1m＝500，C1-3 中kc1m＝2 000.C1，C1-2与C1-3跟踪期望轮廓的实验结果见表3.

从表3可知，调节kc1m的大小仅仅影响到了跟踪控制的效果，轮廓控制性能与之呈现了不相关性，换言之，在正交任务坐标系内轮廓控制与跟踪控制是一对“正交任务”，它们是高度解耦的，因此在调节系统增益时，轮廓控制与跟踪控制可以分别单独考虑，尤其是当需要降低系统增益以换取稳定性时，可以优先减小跟踪控制的增益，这样既可以得到稳定的效果又可以避免轮廓精度的下降.如图11所示为部分参数的自适应估计结果，控制器中的自适应机制增进了控制精度，降低控制器的保守性.

表3 C1，C1-2与C1-3的实验结果Tab.3 Experimental results of C1，C1-2and C1-3

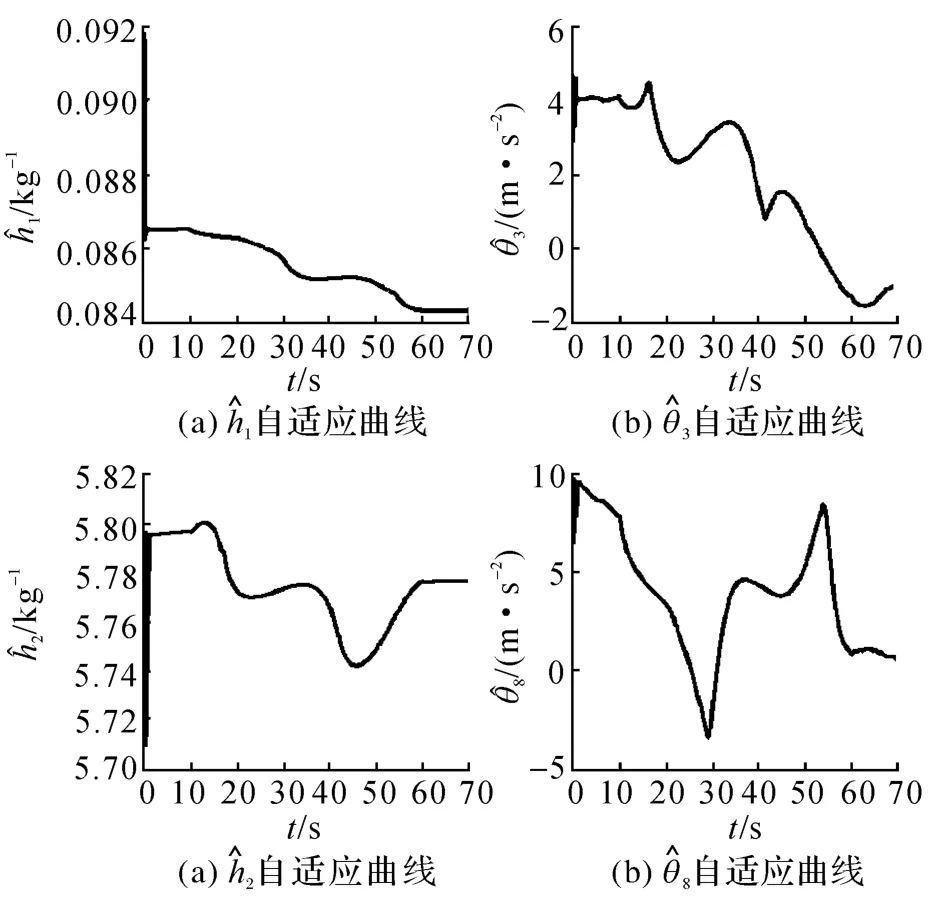
图11 参数估计Fig.11 Parameter estimation

5 结 语

对于二轴电液系统的轮廓运动控制，设计了基于正交全局任务坐标系的非线性自适应鲁棒控制器.与以往的轮廓运动控制器不同，所设计控制器能够在任务空间内精确计算轮廓误差，并在此基础上直接针对轮廓误差与跟踪误差的动力学综合控制律.该控制器把轮廓控制任务与跟踪控制任务高度解耦，因而轮廓控制刚度与跟踪控制刚度可以根据需要独立调节.不仅如此，控制器还融合了自适应控制与鲁棒控制的优点，有效地应对了电液系统中存在的参数不确定性与不确定非线性.该控制器在实验中轮廓控制性能良好、协调性强，实验条件下轮廓误差的均方根值始终保持在15μm 以内.

（

）：

［1］吴爱国，杨硕，张涵，等.多缸锻造液压机的调平和跟踪控制［J］.吉林大学学报：工学版，2014，44（4）：1051-1056.WU Ai-guo，YANG Suo，ZHANG Han，et al.Leveling and tracking control of multi-cylinder forging hydraulic press［J］.Journal of Jilin University：Engineering and Technology Edition，2014，44（4）：1051-1056.

［2］LU X J，HUANG M H.System-decomposition-based multilevel control for hydraulic press machine［J］.IEEE Transactions on Industry Electronics，2012，59（4）：1980-1987.

［3］彭雄斌，龚国芳，陈馈，等.管片拼装机提升缸模糊PID同步控制［J］.浙江大学学报：工学版，2014，48（11）：2002-2008.PENG Xiong-bin，GONG Guo-fang，CHEN Kui，et al.Synchronization fuzzy PID control of lifting hydraulic cylinders for segment erector［J］.Journal of Zhejiang University：Engineering Science，2014，48（11）：2002-2008.

［4］魏建华，国凯，熊义.大型装备多轴电液执行器同步控制［J］.浙江大学学报：工学版，2013，47（5）：755-760.WEI Jian-hua，GUO Kai，XIONG Yi.Synchronized motion control for multi-axis electro-hydraulic system of large equipment［J］.Journal of Zhejiang University：Engineering Science，2013，47（5）：755-760.

［5］MUSIC O，ALLWOOD J M，KAWAI K.A review of the mechanics of metal spinning［J］.Journal of Materials Processing Technology，2010，210（1）：3-23.

［6］赵升吨，赵承伟，王君峰，等.现代旋压设备发展趋势的探讨［J］.中国机械工程，2012，23（10）：1251-1255.ZHAO Sheng-dun，ZHAO Cheng-wei，WANG Junfeng，et al.Discussion about development trends of modern spinning equipment［J］.China Mechanical Engineering，2012，23（10）：1251-1255.

［7］李继贞，韩冬，刘德贵，等.1000kN 大型立式数控强力旋压机［J］.锻压技术，2014，39（2）：1-5.LI Ji-zhen，HAN Dong，LIU De-gui，et al.A large vertical NC power spinning machine of 1000kN ［J］.Forging ＆Stamping Technology，2014，39（2）：1-5.

［8］BUTLER J，TOMIZUKA M.Trajectory planning for high speed multiple axis contouring systems［C］∥Pro-ceedings of the American Control Conference.New York：IEEE，1989：87-94.

［9］YANG J Z，LI Z X.A novel contour error estimation for position loop-based cross-coupled control［J］.IEEE／ASME Transactions on Mechatronics，2011，16（4）：643-655.

［10］CHIU G T C，TOMIZUKA M.Contouring control of machine tool feed drive systems：a task coordinate frame approach［J］.IEEE Transactions on Control Systems Technology，2001，9（1）：130-139.

［11］CHEN C L，LIN K C.Observer-based contouring controller design of a biaxial stage system subject to friction［J］.IEEE Transactions on Control Systems Technology，2001，16（2）：322-329.

［12］YAO B，HU C X，WANG Q F.An orthogonal global task coordinate frame for contouring control of biaxial systems［J］.IEEE／ASME Transactions on Mechatronics，2012，17（4）：622-634.

［13］YAO B，HU C X，WANG Q F.Coordinated adaptive robust contouring controller design for an industrial biaxial precision gantry［J］.IEEE／ASME Transactions on Mechatronics，2012，15（5）：728-735.

［14］胡楚雄.基于全局任务坐标系的精密轮廓运动控制研究［D］.杭州：浙江大学，2010.HU Chu-xiong.Global task coordinate frame based precision contouring motion control［D］.Hangzhou：Zhejiang University，2010.

［15］YAO B，BU F P，Reedy J，et al.Adaptive robust motion control of single-rod hydraulic actuators：theory and experiments ［J］.IEEE／ASME Transactions on Mechatronics，2000，5（1）：79-91.

［16］陈刚，柴毅，魏善碧，等.非线性电液伺服系统的多滑模模糊控制［J］.农业机械学报，2008，39（10）：222-226.CHEN Gang，CAI Yi，WEI Shan-bi，et al.Multiple sliding mode fuzzy control for nonlinear electrohydraulic servo system［J］.Transactions of the Chinese Society for Agricultural Machinery，2008，39（10）：222-226.

［17］KOREN Y，LO C C.Advanced controllers for feed drives［J］.CIRP Proc.-Manufacturing Systems，1992，41（2）：689-698.

［18］BARTON K L，ALLEYNE A G.A cross-coupled iterative learning control design for precision motion control［J］.IEEE Transactions on Control Systems Technology，2008，16（6）：1218-1231.