基于优化顶点弹簧模型的半沉浸环境标定算法

杨廷俊，朱 博，刘 雨

（1.浙江大学 计算机科学与技术学院，浙江 杭州310027；2.浙江大学 航空航天学院，浙江 杭州310027）

沉浸式可视化系统通常被设计为应用虚拟现实技术来模拟真实世界中的各种真实感体验，用户在不需要佩戴任何头戴显示器或其他辅助设备的情形下，便可以在虚拟环境里自由地漫游［1-2］.球幕投影系统作为沉浸式曲面可视化系统代表，通过将观察者包围在减少了边缘干扰的球形屏幕之中，同时对环绕观察者周围的视场进行图像预先扭曲，从而提供了一个具有强烈真实感的可视化环境.早期球幕投影系统的使用场景仅仅局限于天文馆，他们使用多台专门投影硬件，将星空图像和其他类型多媒体资料在球形幕布上投影，进行天文学知识的公共教育领域.随着DLP（digital light procession）投影技术在大型天文馆的广泛应用，通过小型球幕投影系统可以获取昂贵的专业星象球机设备同样的视觉体验，得到了越来越多的关注.小型球幕系统硬件一般由单台商用数字投影机配备普通鱼眼镜头构成，球幕直径常介于2～5m，因而可以在很多场所方便地进行配置.与传统多台投影机构成天文馆系统相比，不需要任何特殊硬件装置，也不需要专门图像融合软件进行拼接，非常适合在科学可视化、模拟仿真环境等场景中进行使用.

对于现有的投影可视化系统，由于投影表面形状和投影机安装位置等因素，图像在投影到投影表面时常会出现扭曲现象，几何标定是通过对该扭曲参数进行估计，实现对投影图像的预先校正工作［3］.目前，大多数投影系统都广泛采用基于相机反馈辅助的标定算法，将平面屏幕系统中的该问题转换为相机和投影机之间单向性矩阵的计算［4-6］.对于曲面和非平面屏幕系统，几何标定不能由单一的单线性矩阵描述，Raskar等［7-9］使用一对正交的立体照相机，并通过保角映射和二次传递的方法来进行标定，该方法仅适用于标准二次曲面.Majumder等［10-12］使用单台相机并通过有理贝塞尔面片的方法对CAVE和球幕系统进行几何标定；该方法要求投影表面为标准球幕表面，并需要在投影表面放置物理的校正标记.

针对现有曲面投影环境标定算法在自适应校正精度和计算效率上的不足，本文提出一种基于优化顶点弹簧模型的半沉浸式投影环境快速自适应标定算法.首先基于优化的顶点弹簧模型对非均匀二次曲面进行三维网格获取；然后，使用曲面细分方法根据人眼视线与网格面片的空间几何关系，对网格进行进一步的网格细分计算；最终根据细分结果，网格对投影图像进行精确预校正，实现半沉浸式投影环境的快速自适应标定.

1 基于球幕的半沉浸可视化系统建模

1.1 非均匀二次球形曲面数学模型

基于球形幕布投影的半沉浸式可视化环境需要应用非均匀曲面网格的精确计算.为了分析球面投影图像的变形情况需要建立非均匀二次球面投影模型，可以将球面屏幕简化为一个球面，投影机的投影光线简化为一个四棱锥体.如图1所示，投影机的投影位置在z轴上的P 点，投影机的投影方向通过球心O，则投影机的投影光束呈一个四棱锥形，它与球面相交，在球面上生成一个比较规则的准矩形曲面，即投影光束所形成的四棱锥体为P-Q1Q2Q3Q4.

假设球体的半径为R，则球面上的坐标点（x，y，z）可以用参数化的经纬坐标（θ，φ）表示为

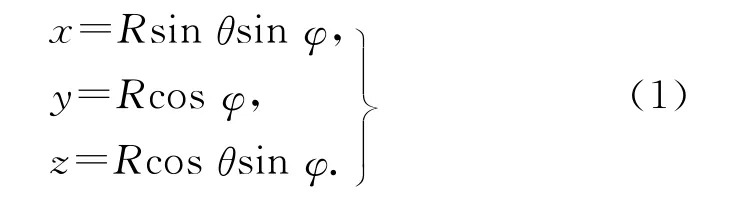
为了简化投影光束的表达，将投影机投影光束的边界表示为4 个平面，采用4 个方程来表示.PQ1Q2、PQ3Q4、PQ2Q4和PQ4Q1平 面 的 表 达 式分别为

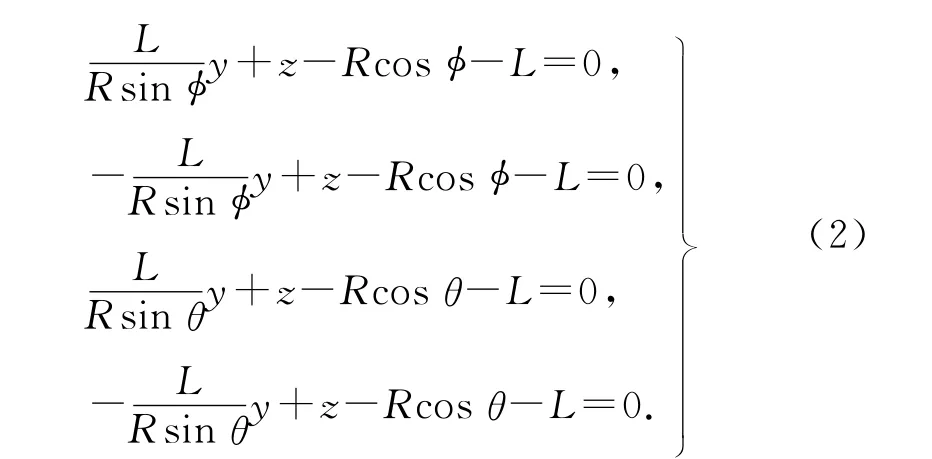
式中：L 为投影机与球面的成像距离.

图1 球形曲面投影模型Fig.1 Spherical projection model

1.2 鱼眼光学系统

本文设计的球幕投影系统使用加装鱼眼镜头的方式组成投影光学系统进行投影成像（见图2（a））.鱼眼镜头成像的球面投影模型（见图2（b）），其定义为从原点O 指向空间任一点A（x，y，z）的射线斜交投影球面于一点.将这一点正投影到一个与z 轴垂直的固定平面上（由于该平面上各点的z 坐标相同，只考虑x 和y 坐标），得到平面点B（m，n）.空间各点A（x，y，z）在所给固定平面上的投影B（m，n）即构成鱼眼镜头成像，利用该模型的逆变换可以将鱼眼镜头图像变换为透视投影图像.

图2 鱼眼镜头投影系统Fig.2 Fisheye lens projection system

利用鱼眼镜头可以得到180°高汇聚和大视角的圆形鱼眼图像，反之180°圆形鱼眼图像的大视角和高汇聚性通过180°鱼眼投影镜头从投影到球面便能将景深部分信息还原（见图3）.这种鱼眼投影配合球形曲面投影系统给人造成的视觉误差，能够让人产生如临现场的沉浸感.

图3 鱼眼镜头投影示例Fig.3 Fisheye lens projection example

2 基于优化顶点弹簧模型的自适应快速标定算法

2.1 顶点弹簧网格变形方法

顶点弹簧模型（vertex springs model）是非结构动网格弹簧近似法的一种.假设将网格单元的各条边看作弹簧，则弹簧系数与网格边的长度有关.当网格边界发生自适应移动后，通过求解弹簧系统节点受力平衡确定网格点的新位置.该非结构动网格变形方法通过网格变形、网格重构和局部网格重构等方法使计算网格适应计算区域的改变，是一种非定常问题数值模拟的关键技术，可以应用于可变形飞行器、机翼气动弹性振动、生物仿生流等问题所涉及的非定常问题求解.

本文研究的基于球形幕布投影的半沉浸式可视化环境需要进行非均匀曲面网格的精确计算，应用非结构动网格变形方法可以在保持网格数目不变的情况下，通过网格结构变形来适应运动边界引起的物理空间变化.变形动网格可以针对球幕曲面环境的物理性质，建立有效控制网格变形和运动的计算模型.基于顶点弹簧模型的非结构网格具有几何上的灵活性，易于处理复杂曲面形状模型，同时网格生成的自动化程度高.球幕的有效投影环境边界获取之后，在计算网格区域内可以自动生成网格，当网格边界发生改变时，运动边界带动有效网格区域内的网格节点运动，依靠网格边的伸缩、扭转来适应边界的运动.

基于顶点弹簧模型的网格变形计算如图4 所示，其中图4（a）所示为非结构网格的示例图.弹簧法假设网格节点由弹簧连接，整个计算域网格是一个达到平衡状态的弹簧系统.

如图4（b）所示为非结构网格局部放大的顶点弹簧模型示例图，网格边可以看作弹簧连接，连同节点i、j间的组成顶点弹簧变形模型.获得由于边界变形或运动带来的网格节点位移，从而得到适应计算域变化的计算网格.其中将网格边看作弹簧，节点i、j之间的弹簧张力计算为

式中：Kij为弹簧的倔强系数，xi、xj分别为节点i、j的位置矢量.节点i所受的合力如式（4）所示，其中Ni为与节点i相连的相邻节点总数.

在初始网格确定后，使用式（4）得到节点i的初始状态，则运动边界上的点移动后，可以构造线性方程得到其他网格点的新位置坐标：

图4 顶点弹簧模型Fig.4 Vertex springs model

式中：下标npsum 为运动边界点数量.分析上述线性方程，由于对角线元素求和指标j取遍该行所有非对角线不为0的列k，因此该方程对角占优，采用Jacobi迭代格式收敛如下公式：

2.2 基于优化顶点弹簧模型的球幕网格计算

如图5（a）所示为球幕网格示例，将最外围的球幕网格边缘作为网格变形边界，根据实际球幕的物理几何形状来不断地变化边界节点.从图5（b）可以看出，网格节点之间的连接是不等长线段，需要求解图4（b）中的球幕网格的弹簧倔强系数Kij.

根据顶点弹簧模型（式（7）），可以将弹簧倔强系数设置为常数，网格点以东后的新位置坐标可以通过周围点坐标的双线性插值计算得到.常用的弹簧倔强系数计算与网格节点之间的距离成倒数，对于球幕网格可以应用二维顶点弹簧倔强系数计算公式：

式中：lij为节点i、j之间的距离.当网格不断压缩变形时，倔强系数不断增大，保证球幕网格节点之间保持一定的间距.在实际计算过程中会出现如图6所示不可预知的“网格拆穿”（mesh snap-through），根据顶点弹簧模型在整体球幕网格的作用力，这种牵引作用距离边界越远影响越小，最早发生网格变形失败的网格单元一般位于网格边缘附近.

图5 球幕网格示例图Fig.5 Dome mesh example

图6 顶点弹簧模型的“网格拆穿”Fig.6 “Mesh snap-through”in vertex springs model

为了解决上述网格拆穿情况，对经典顶点弹簧倔强系数计算方法进行改进，优化的倔强系数计算方法综合考虑网格的伸缩和扭转作用，引入网格变形修正因子S1和S2.其中，S1是一个与网格边界相关的空间位置函数，可以通过椭圆方程计算得到，由于球幕网格的特殊形状，可以设置为一个常数.S2是二维网格扭转因子，可以由下式计算得到：

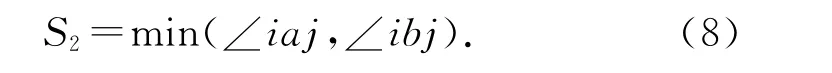
最终优化的适用于球幕网格的顶点弹簧倔强系数计算公式如下：

随着网格节点之间的距离和夹角变化，lij和S2不断变化，倔强系数需要实时更新.

在实际计算中，弹簧网格中的实时受力状况与初始受力相同，则第i个节点在网格弹簧系统中所受的合力仅需计算一次，在计算过程中保持不变.对于优化的弹簧倔强系数需要按照一定的频率刷新，可以迭代100步以上更新一次，基于以上算法实现的球幕网格计算步骤具体如下.

1）使用“投影机-相机”系统获取球幕环境的采集图像，应用Sobel分割算法和图像二值化算法提取球幕边缘，得到球幕边缘坐标集合.

2）绘制原始球幕网格图形作为初始网格，通过式（9）计算得到优化后的初始倔强系数，最终构造顶点弹簧模型.

3）结合步骤1）计算得到的球幕边缘坐标，使用顶点弹簧模型建立网格弹簧系统方程，得到网格内所有节点的新坐标集合.

4）通过“投影机-相机”系统进行球幕网格校正图像反馈，多步迭代计算节点坐标并更新.

5）通过步骤3）建立的线性方程迭代收敛，并实时使用4）的实时在线闭环系统进行校正结果反馈，最终校正球幕网格.

2.3 基于曲面细分算法和GPU 加速的球幕校正投影图形渲染

由于在鱼眼镜头的投影模式下，球幕几何网格中任意一条边上的2个顶点之间，其距离并非原始投影之前的直线关系，而是经过鱼眼透视的空间曲线；对于球幕投影中人眼观察到的球幕表面区域，为了提高鱼眼投影校正的精度，四边形网格需要被进一步细化.从OpenGL 4.0［13］标准以及DirectX 11.0［14］开始，基于硬件的参数表面曲面细分技术便被引入了新一代显卡的可编程图形流水线中.

本文的研究工作均使用OpenGL来实现，因此接下来的内容均只介绍OpenGL中的实现方法.在加入了曲面细分的硬件支持之后，目前OpenGL 4.0以上标准中的GPU 的绘制流水线如图7 所示.在该绘制流水线中，硬件曲面细分工作包含了图中蓝色的3个单元：细分控制着色器（TCS）、细分图元产生器（TGP）和细分评估着色器（TES）.TCS根据细分参数对片元的属性及内部的顶点属性进行修改；TGP单元根据下一单元TES的输入数据格式，将对TCS传入的片元内部的顶点进行分割；TES 将TGP分割后每个顶点的局部坐标变换成世界坐标，并对顶点的相应属性进行转换.

在球幕投影系统中，为了减少更精细网格数据的存储和CPU（中央处理器）／GPU 的总线开销，利用显卡中的独立功能硬件进行曲面细分.根据网格面片与人眼视线方向的夹角作为参数描述，在需要细分网格的区域生成密集的三角化面片：网格面片与人眼视线方向的夹角越小，人眼对于鱼眼投影失真的容忍度越小，网格曲面需要细分的精度越大；网格与视线的夹角越大，人眼对于其绘制效果的敏感度越低，网格细分的精度越小.细分参数的计算如下：

式中：dm为单个网格的细分参数，Nm为网格面片的归一化法向向量，dmax为细分参数的最大值，z 为人离球幕的距离，c为人眼所在的位置，ov为人眼视线与球幕交点的位置.

对于网格细分算法，为了更好地利用以上的曲面细分绘制流水线，减少网格数据的复杂度，并避免细分算法的迭代情况出现，选择PN（Point-Normal）三角细分算法.PN 三角细分法是Vlachos等［15］提出的一种基于三角化网格的曲面细分方法，它通过一种特殊的贝塞尔曲面来替换原始的三角网格.对于任意的三角面片，输入顶点Vi＝（Pi，Ni），其中Pi为顶点位置，Ni为顶点对应的法线向量；新顶点的重心坐标u、v、w∈R3，该细分法产生的细分曲面可以表示为

图7 基于曲面细分算法的GPU 图形绘制流水线Fig.7 Graphics pipeline for hardware tessellation

式中：u ＋v ＋w ＝1；bijk为PN 三角片的控制点，如图8所示，计算公式如下：

图8 PN 三角细分法Fig.8 Curved PN triangles

为了减少基于视点的曲面细分过程中，频繁使用曲面细分带来的额外计算负荷，本文利用了OpenGL 4.0新流水线下的另一新特性：Transform Feedback技术［16］.所谓Transform Feedback，即对当前在GPU 流水线上的顶点数据，在经过顶点处理和曲面细分等处理后，进入到光栅化步骤之前，将之前流水线处理的结果数据，保存到缓存结构中.在本文的球幕网格校正系统中，基于Transform Feedback使用了Two-Pass的绘制策略：当用户视点发生改变时，进行一次曲面细分，并将细分结果保存在显卡内存中，并在下一次用户视点变化之前，一直使用之前曲面细分的结果网格，进行球幕图像的绘制；当用户视点再次改变时，根据新的视线方向，对初始的稀疏网格进行再一次的细分，从而减少重复的顶点数据处理和增加绘制性能.

3 算法实现和验证

为了评估基于优化顶点弹簧模型的快速自适应标定算法效果，搭建了单台投影机组成的小型球幕实验环境：幕布采用直径为2m 的一体成型半球型无缝正投球幕；投影机使用物理分辨率为1 920×1 080的DLP投影机；鱼眼镜头采用基于等距投影映射模式的Peleng 8mm f／3.5镜头；相机使用罗技QuickCam Pro 9000型号摄像头；标定计算的电脑显卡使用Nvidia GTX 750，其支持CUDA（Compute Unified Device Architecture）技术和OpenGL 4.0标准.如图9所示为本文提出的基于优化顶点弹簧模型的快速自适应标定算法实现和验证实验.

图9（b）展示了整个实验的硬件环境，其中，鱼眼镜头与投影机镜头位于同一光轴线上，由于从鱼眼镜头出射的光线能够覆盖180°的视场，整个投影球幕都位于覆盖范围之内.根据该标定算法的计算步骤可知，整个标定的过程如下.

1）使用相机获取球幕环境的采集图像，利用图像分割算法得到球幕边缘.

2）绘制原始球幕网格图形作为初始网格，并构造顶点弹簧模型，图9（b）展示了初始网格的投影效果.

3）通过“投影机-相机”系统和球幕边缘的位置信息，进行球幕网格的弹簧模型迭代更新，图9（c）展示了通过多次迭代计算的最终效果.

4）利用GPU 图形硬件的曲面细分功能，根据网格面片与人眼视线的关系，进行自适应的网格细分，图9（d）展示了经过曲面细分后的网格结果.

将标定结果应用到球幕投影的图像渲染，如图9（e）、（f）分别为图片播放和模拟飞行的效果图.

为了验证本文提出的快速自适应标定算法的校正精度和效率，使用几种现有的主流球幕投影系统校正方法［17-18］进行实验比较，算法的比较结果如表1所示.

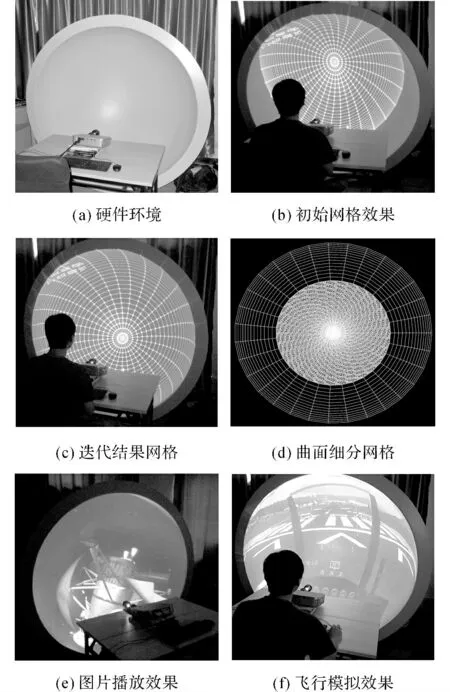
图9 本文提出的标定算法实现和验证实验Fig.9 Implementation and experimental validation of proposed calibration algorithm

表1 算法实验比较结果Tab.1 Comparison of results

与激光网格标定方法和有理贝塞尔曲面标定算法这2种现有主流的球幕标定方法相比，使用本文提出的基于优化顶点弹簧模型的球幕标定算法可以从3个方面体现出明显优势.1）在投影模式上，由于多投影机拼接系统不仅需要多台高流明的工业投影机，还需要额外图形融合硬件进行多通道融合工作；使用单投影机投影在工程造价上远小于多投影机拼接方法，可以大大降低球幕投影设备的硬件成本.2）在校正精度上，由于多投影机拼接本身的复杂性以及投影机光学投影硬件本身的关系，不同投影机很可能出现颜色空间和亮度空间不统一的现象，相邻投影机投影区域之间的裂缝和颜色跳变，很容易造成视觉感知的敏感；本文提出的单投影机标定算法不仅可以达到低于0.5像素的校正精度，小于等于原有多投影机标定算法中的最高校正精度，并且由于单投影机的色彩分布更加均匀，能够给用户提供更好的视觉体验.3）在校正效率上，多投影机拼接系统需要水平仪或其他辅助设备进行精密测量，同时需要投入具有深厚工程经验的技术人员进行操作校正软件，不仅降低了系统的易用性，而且加大了整个校正过程的时间；本文提出的基于优化顶点弹簧模型的算法，整体标定时间小于3min，低于原有方法中至少5min的校正时间需求.

4 结 语

本文针对半沉浸式投影环境的标定计算提出一种基于优化顶点弹簧模型的自适应快速校正算法.该算法基于球幕投影过程中由于镜头光线传输和曲面投影表面引起的扭曲现象，借助“投影机-相机”构成的光学反馈系统，通过对弹簧模型的不断迭代和更新工作，能够快速、方便地完成整个球幕的粗粒度校正操作；然后对人眼视线对应的需要高精度网格的敏感区域，通过基于图形硬件加速的曲面细分技术，结合PN 三角面片细分方法，使用更加精细的贝塞尔曲面来对投影曲面进行细分模拟.

算法验证和比较实验结果表明，使用本文提出的基于优化顶点弹簧模型的自适应快速标定方法可以显著地加速球幕投影系统的整体校正效率，同时大幅提升投影图像的校正精度，并且在降低球幕投影系统硬件成本的同时得到了符合视觉检验的投影图像校正效果.下一阶段的工作将集中在全沉浸式球幕标定方法以及基于球幕投影系统的虚拟现实技术的研究2个方面，希望在未来的工作中逐步完善球幕投影系统的应用，为沉浸式虚拟现实环境提供一种新型的可视化技术.

（

）：

［1］DEFANTI T A，SANDIN D J，CRUZ-NEIRA C.A“room”with a “view”［J］.IEEE Spectrum，1993，30（10）：30-33.

［2］CRUZ-NEIRA C，SANDIN D J，DEFANTI T A，et al.The CAVE audio visual experience automatic virtual environment［J］.Communnications of the ACM，1992，35（6）：64-72.

［3］HARVILLE M，CULBERTSON B，SOBEL I，et al.Practical methods for geometric and photometric correction of tiled projector displays on curved surfaces［C］∥Proceedings of CVPRW.New York：IEEE，2006：52-59.

［4］BROWN M，MAJUMDER A，YANG R.Camera-based calibration techniques for seamless multi-projector displays［J］.IEEE Transactions on Visualization and Computer Graphics，2005，11（2）：193-206.

［5］SUKTHANKAR R，STOCKTON R G，MULLIN M D.Smarter presentations：exploiting homography in camera-projector systems［C］∥Proceddings of the 8th International Conference on Computer Vision （ICCV-01）.Vancouver：IEEE，2001：247-253.

［6］OKATANI T，DEGUCHI K.Autocalibration of a projector-camera system［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（12）：1845-1855.

［7］RASKAR R，BAAR J，RAO S，et al.Multi-projector imagery on curved surfaces［R］.Cambridge：Mitsubishi Electric Research Labs，2004.

［8］BAAR J，RASKAR R.Flexible calibration of multiple projectors for low-cost curved screen displays ［C］∥Proceddings of 14th International Conference on Artificial Reality Telexistence.Seoul：［s.n.］，2004：263-268.

［9］RASKAR R，BAAR J，WILLARCHER T，et al.Quadric transfer for immersive curved screen displays［J］.Computer Graphics Forum，2004，23（3）：451-460.

［10］SAJADI B，MAJUMDER A.Automatic registration of multiple projectors on swept surfaces［C］∥Proceddings of 17th ACM Symposium on Virtual Reality Software and Technology. Hong Kong：ACM，2010：159-166.

［11］SAJADI B，MAJUMDER A.Auto-calibration of multi-projector CAVE-like immersive environments［J］.IEEE Transaction on Visualization and Computer Graphics，2012，18（3）：381-393.

［12］SAJADI B，MAJUMDER A.Automatic registration of multi-projector domes using a single uncalibrated camera［J］.Compututer Graphics Forum，2011，30（3）：1161-1170.

［13］SEGAL M，AKELEY K.OpenGL 4.0specification［M］.［S.l.］：Khronos Group Inc，2010.

［14］SHERROD A，JONES W.Beginning DirectX 11game programming［M］.Boston：Cengage Learning，2011.

［15］VLACHOS A，PETERS J，BOYD C，et al.Curved PN triangles［C］∥Proceedings of the 2001Symposium on Interactive 3D Graphics.New York：ACM，2001：159-166.

［16］ROST R，LICEA-KANE B.OpenGL shading language［M］.3rd ed.Boston：Wesley，2010.

［17］李赛.面向大型遗址的球幕展示系统研究与实现［D］.杭州：浙江大学，2012.LI Sai.Dome display systems research and implementation for large sites［D］.Hangzhou：Zhejiang University，2012.

［18］梁思毓.面向球幕的编辑式多投影校正技术与系统［D］.上海：复旦大学，2012.LIANG Si-yu.Multiple projection calibration technology based on interactive editing for dome systems［D］.Shanghai：Fudan University，2012.